2. Исчисление предикатов. Теория классов.

Рассмотрим исчисление унарных предикатов. Формальная аксиоматическая система в этом случае называется теорией классов (типов, категорий). Впервые теория классов была сформулирована и использована для ведения публичных споров Аристотелем. В настоящее время она получила «второе дыхание» и была усовершенствована для применения в объектно-ориентированных языках (при построении формальной семантики), базах знаний (в фреймовых системах), построении хранилищ данных (Data Ware Haus – DWH), методов построения семантических профилей (набора свойств) типовых объектов и их поиска в сверхбольших массивах данных (Data Mining).

1. Базовые утверждения (высказывания) теории классов.

Утверждения рассматривают отношения между двумя объектами S и Р. S и Р являются классами, а «S» и «Р» являются именами классов. Структура утверждения – «S есть Р», где S называется субъектом, а Р предикатом (свойством). Всего различных типов утверждений – 4.

1. Общеутвердительное (А) – Всякий предмет х из S есть всякий предмет из Р. (Всякий ромб есть параллелограмм).

Формула –.

2. Общеотрицательные (Е) – Всякий S не есть Р. (Всякий треугольник не есть ромб).

Формула – .

3. Частноутвердительные (I ) – некоторые S есть Р. (Некоторые параллелограммы есть ромбы).

Формула – .

4. Частноотрицательное (О) – Некоторые S не есть Р. (Некоторые параллелограммы не есть ромбы).

Формула – .

2. Правильно построенные рассуждения в теории

классов.

Структура рассуждения: имеет содержательную интерпретацию «из R следует P». Посылок может быть несколько, все суть базовые утверждения, следствие – единственное базовое утверждение. Рассуждение называется правильным или силлогизмом, если оно тождественно истинно (общезначимо) при любых интерпретациях. «» называется выводом (дедукцией) из посылок R, (пишется R ├ P либо R  P ), если есть силлогизм. Знак «├» вывода интерпретируется логической операцией «» импликации (следования). Правильный вывод (рассуждение): из истинности посылки R следует истинный вывод P. При интерпретации силлогизма логической операцией импликации: . В зависимости от количества посылок силлогизмы могут быть 0, 1, 2, и т.д. рангов.

3. Логические законы теории классов – (0-й ранг).

Законы считаются изначально выводимыми (аксиомами), пишется «├ Р». Имеется всего три закона 0-го ранга.

1. ├ Закон тождества. Всякий обладает свойством S.

2. ├ Закон противоречия. Невозможна ситуация, когда предметы из класса S входят в Р (см. таблицу жердановых интерпретаций) и не входят в Р.

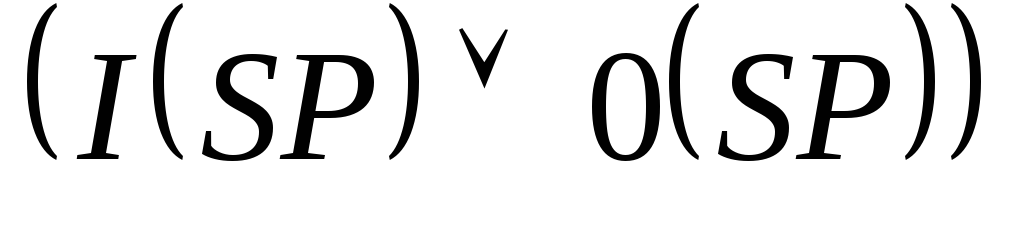3. ├ Закон исключённого третьего. Для каждой конкретной сущности х, входящей в S, истинно одно из утверждений: «х входит в Р или х не входит в Р».

Если отменить закон исключённого третьего, то можно построить т. н. интуиционистскую логику.

4. Интерпретация базовых утверждений.

Предметные области (семантика), которые могут служить для интерпретации утверждений о классах различны. Даже содержательных предметных областей может быть бесконечное множество.

Для интерпретации утверждений (высказываний) в теории классов выбраны т.н. Жердановы соотношения (Жердан – французский математик; исследовал теорию классов в 1947 – 1953), которые связывают два класса множеств предметов: класс S и класс Р.

Четыре Жердановых соотношения (интерпретации).

пересечение независимость включение тождество

классов классов классов классов

Жерданова таблица интерпретации утверждений.

Содержит истинность/ложность каждого базового утверждения.