Потенциал диполя

Применим полученные данные для вычисления потенциала диполя.

Диполемназываются два связанных электрических разноименных заряда, находящихся на расстоянии, где вектор(плечо диполя) направлен отк.

Момент диполя .

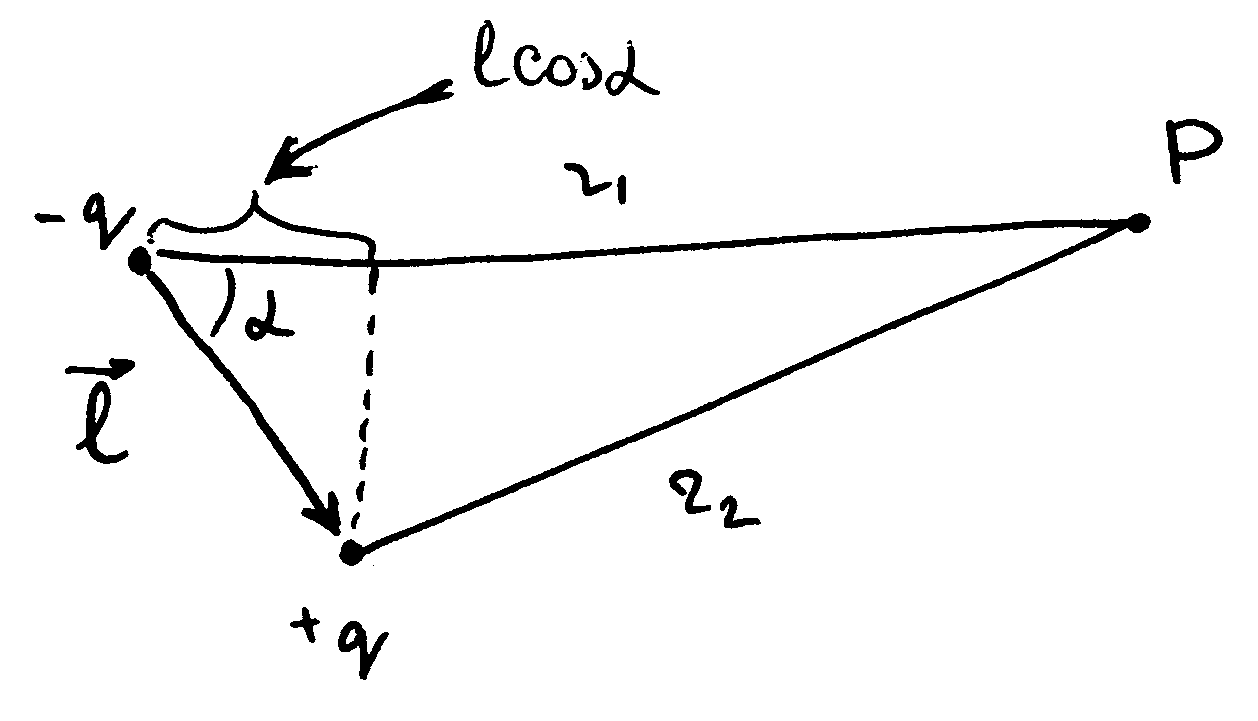
РИС.15-2

В соответствии с принципом суперпозиции полей:

.

Если , то рассматриваемая система зарядов называетсяточечным диполем.

При выполнении этого условия ,.

, где - момент диполя.

Напряженность электрического поля диполя

- к нему неприменима электростатическая теорема Гаусса!

Термоэлектронный ток между двумя бесконечными плоскими электродами в вакууме.Формула Лэнгмюра.

Полагаем, что при фиксированном потенциал поине меняется. Следовательно, эквипотенциальные поверхности – это плоскости, параллельные катоду и аноду.

Уравнение Пуассона сводится к одномерному:

.

Так как электрон заряжен отрицательно, плотность объемных зарядов: .

РИС.15-3

Теперь уравнение имеет вид:

.

Поле между электродами совершает работу , которая переходит в кинетическую энергию движения электронов:

.

Плотность электронного тока:

.

В стационарном состоянии плотность тока от координат не зависит. Определим отсюда концентрацию электронов:

и подставим полученный результат в уравнение:

, а сюда подставим .

Получим:

.

если обозначить , то уравнение, которое необходимо решить,

- величины перед отне зависят.

Решение этого уравнения: .

Можно убедиться в правильности этого решения путем непосредственной подстановки в уравнение.

Граничные условия задачи:

1. Поле вблизи катода равно нулю: при.

2. Катод заземлен (в практических задачах всегда полагают потенциал Земли =0): при.

3. Потенциал анода: при.

; ;(закон «3/2»).

РИС.15-4

- можно говорить напряжение на аноде, так как потенциал катода равен нулю.

Сдвиг (влево от нуля) обусловлен тем, что вылетающие из катода электроны имеют , и нужно приложить тормозящее поле, чтобы они не долетели до анода.

Поле в проводниках

Поле внутри проводника равно нулю. Если внутри проводника в какой-либо точке возникает электрическое поле , то возникает упорядоченное движение зарядов, т. е. электрический ток. Носители заряда – электроны (или дырки), отрицательные или положительные ионы.

Если прохождение тока не связано с переносом вещества, то проводник является электронным, если связано, то ионная проводимость (такова обычно проводимость электролитов, газов, некоторых твердых тел).

В металлах проводимость обычно электронная (или дырочная).

Определение:

Если прохождение тока не связано спереносом массы, то такой проводник называют электронным (дырочным).

Riecke E. (1901 г.): в течение года пропускал электрический ток через три поставленных друг на друга цилиндра - медный, алюминиевый и медный. Количество протекшего электричества было равно 3448800 Кл. Тем не менее цилиндры сохранили свой вес с точностью до0,03 мг. Отсюда следует, что металлы обладают электронной проводимостью.

Опытный закон Ома: . Внутри проводника, следовательно,(где- произвольная замкнутая поверхность внутри проводника). Отсюда по теореме Гаусса(- плотность объемных зарядов), точнее, положительные и отрицательные заряды компенсируются, а все свободные заряды размещаются на границах раздела или на иных неоднородностях.

Если внутри проводника в какой-либо точке в некоторый момент времени t=t₀возникает электрическое полеE, то сразу возникает упорядоченное движение зарядов: локальный ток. Вследствие этого плотность свободных зарядов уменьшается по закону:

, где -Максвеллово время релаксации.

Максвеллово время релаксации –показывает, в течение какого промежутка времени плотность свободных объемных зарядов уменьшится вe –раз.

Если =10^-14Ом^-1см^-1(типичный диэлектрик), то это время составляет 310⁶лет. Для металлов –10^-12с. Значит за это время поле в металле уменьшится до нуля.

Следствие.внутри проводника. Но, следовательно,на всем протяжении данного проводника (при отсутствии сторонних эдс). Все части проводника имеют одинаковый потенциал.

Внутренняя поверхность металлического шара . Значит, внутри полостии.