Формальная алгебра A, f1, f2 , fm |
|
A – Множество. Операции i |
fi A( Ani ) |
Простейший случай (кроме унарных): Бинарная алгебра с одной операцией
A, f & f AA A
Инфиксная запись: x y = f(x, y)
A, = A, f (f AA A & ( x A y A x y = f(x, y)))
Моделирует преобразование символьной информации
x |
|
x y |
y |
|
Формы представления
Таблица Кэли
A, , A={a,b,c,d}
type
TA = (a,b,c,d); const
AOp: array [a..d,a..d] of TA = ((a,b,c,d),
(b,a,d,c),
(c,d,b,a),
(d,c,a,b));
function fAOp(x,y:TA):TA; fAOP:=AOp[x,y];
end;
Реализация (варианты): |
X |
|
|
|
|
P0 |
|
||||
|
|
|
|
|
|||||||
Программа: Инициализированный |
|
|
X0 |
P0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
P1 |
|
|||||||||
|
|
X1 |
P1 |
|
|
|
|||||
|
|
|
|
|
|||||||
|
P2 |
|
|||||||||
массив-константа |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y0 |
P2 |
|
|
P3 |
|
||||
|
|
|
|
|
|||||||
Аппаратура: Постоянная память |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
Y1 |
P3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Коды: a=00, b=01, c=10, d=11 |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A3..A0 |
D1..D0 |
|
|
0000 |
00 |
|
|
0001 |
01 |
|
|
0010 |
10 |
|
|
0011 |
11 |
|
|
0100 |
01 |
|
|
0101 |
00 |
|
|
0110 |
11 |
|
|
0111 |
10 |
|
|
1000 |
10 |
|
|
1001 |
11 |
|
|
1010 |
01 |
|
|
1011 |
00 |
|
|
1100 |
11 |
|
|
1101 |
10 |
|
|
1110 |
00 |
|
|
1111 |
01 |
|
A0 |
D0 |
Z0 |
|
Z1 |
|||
A1 |
D1 |
||
|
|||
A2 |
|
||
|
|
||
A3 |
|
Z |
|
|
|
||
OE |
|
|
|
CS |
|
|
Изоморфизм бинарных алгебр – одинаковость структур
A, ~ B, ▫ ( f BA ( f -1 AB ) & ( x A y A ( f(x y)=f(x)▫f(y) ))
Пример: Двойственные логические операции
Формула Де-Моргана:
={0, 1} x y ( (x & y) = x y )
Определение двойственной операции:
x ▫ y = ( x y)
Схема замены:
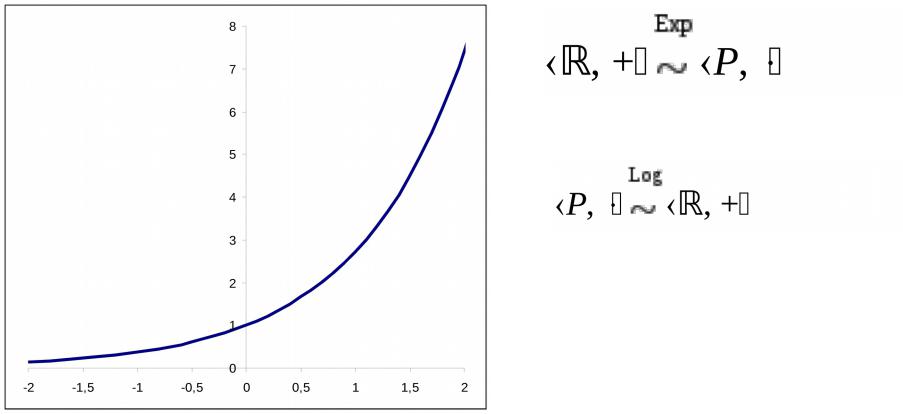
Пример изоморфизма в математике: логарифмическая линейка
Множество действительных чисел
Множество положительных действительных чисел P={x | x & x>0}
Алгебры сложения и умножения: , + и P,
Соотношение изоморфизма: x y Exp(x+y) = Exp(x) Exp(y)
Обратно
x P y P
Log(x y) = Log(x)+Log(y)
Изоморфизм алгебр – отношение эквивалентности
Класс эквивалентности по отношению изоморфизма некоторой алгебры [ A, ]~ называют абстрактной
(свободной) алгеброй.
Пример: все классы двухэлементных бинарных алгебр
M – множество всех бинарных операций на двоичном множестве = {0, 1} M = { , | , = , f & ( f ) & ( = {0, 1})}
Множество всех классов M/~ – разбиение M.
Обозначим |
10 классов логических операций |
|
|
||
|
|
|
|
|
|
алгебру только |
|
|
|
Пример: |
|
|
|
|
|
||
содержимым |
|
|
|
|
|
таблицы (без |
a |
b |
|
0 |
1 |
заголовков) – они |
|
||||
c |
d |
|
1 |
1 |
|
одинаковые у |
|
||||
всех алгебр из M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изоморфные пары схемы |
a |
b |
~ |
d |
c |
|
||||||||||
|
|
|
c |
d |
b |
a |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 0 |
|
Константы |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
~ |
1 |
1 |
|
|
4 |
1 |
0 |
↓ и | |
1 |
1 |
|
|||||||
0 |
0 |
1 |
1 |
|
|
|
|
|
~ |
|
|||||||||
|
|
|
|
|
0 |
0 |
|
1 |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
& и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
5 |
|
|
и |
|
|
|
|||||||
0 |
0 |
|
~ |
0 |
1 |
|
|
0 0 |
1 0 |
|
|||||||||
0 |
1 |
|
1 |
1 |
|
|
|
|
1 |
0 |
|
~ |
1 |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 0 |
1 |
и |
1 |
0 |
|
|
6 0 1 |
и → |
1 1 |
|
|||||||||
1 |
0 |
|
~ |
0 |
1 |
|
|
|
|
0 |
0 |
|
~ |
0 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самодвойственные |
||||
7 |
1 |
1 |
~ |
1 |
1 |
|
0 |
0 |
0 |
0 |
|
|
|
||||
8 |
0 |
0 |
~ |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
|
|
||||
9 |
1 |
0 |
~ |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
|
|
||||
10 |
0 |
1 |
~ |
0 |
1 |
|
0 |
1 |
0 |
1 |
|
|
|
||||
Рассматриваемые специальные свойства (классификационные признаки) Наличие или отсутствие специальных свойств у операции
Наличие или отсутствие элементов со специальными свойствами
Примеры алгебр со специальными свойствами операций и элементов
Ассоциативная алгебра a (b c) = (a b) c
eL eR e 0 :
x 0 x x 0 x
Ассоциативная алгебра классов вычетов по модулю 3: 3,+
eL eR e 0 :
x [0] x x [0] x
Импликация не ассоциативна
eL 1 |
|
|
0 |
1 |
||
|
||||||
x 1 x x |
|
|
|
|
|
|
|
0 |
|
1 |
1 |
||
eR x x eR x |
1 |
|
0 |
1 |
||
|
|
|||||
0 (0 0) 0 1 1 (0 0) 0 1 0 0
0 (0 0) (0 0) 0
0 1
0 1 0
1 0 0
Нет нейтральных элементов
0 1
0 0 1
1 0 1
Два левых нейтральных элемента
eL 0, eL / 1
Единственность двустороннего нейтрального элемента
0 1
0 0 1
1 0 1
eL 0, |
eL / 1 |
Нет правых нейтральных |
Нулевые элементы
0 1
|
|
|
|
oL oR 1 |
||
0 |
0 |
1 |
||||
x |
1 x x 1 1 |
|||||
1 |
1 |
1 |
||||
|
|
|||||