
- •Введение в помехоустойчивое кодирование
- •Функциональная схема процесса повышения достоверности
- •Двоичное блоковое кодирование
- •Двоичный блоковый (n, k) код
- •Структура декодирующего устройства
- •Геометрическая интерпретация вероятности
- •Независимость событий A и B
- •Геометрическая интерпретация формул полной вероятности и формул Байеса для вычисления вероятностей гипотез
- •Оценивание по принципу максимального правдоподобия
- •Оценивание по принципу максимального правдоподобия
- •Другие возможные соображения по выбору правил принятия решений.
- •Алгебраическая модель представления искажений при передаче двоичного вектора по ненадежному каналу
- •Некоторые новые обозначения
- •Некоторые упрощения для варианта оценивания по максимуму правдоподобия
- •Декодирование по минимуму расстояния
- •Пример декодирования по минимуму расстояния: распознавание написания цифр почтового индекса.
- •Исправление ошибок считывания
- •Двоичные групповые коды
- •Матричное кодирование – способ построения группового кода.
- •Систематический код
- •Замкнутое множество допустимых кодовых слов
- •Разбиение множества двоичных векторов на смежные классы по подгруппе допустимых кодовых слов и
- •Таблица стандартной расстановки
- •Выбор образующих элементов – лидеров классов
- •Иллюстрация к схеме декодирования посредством лидеров классов.
- •Пример декодирования посредством лидеров для (6,3) кода
- •Декодирование посредством лидеров следует правилу декодирования по минимуму расстояния.
- •Варианты построения декодера
- •Проверочная матрица для систематического кода
- •Примеры вычисления значений синдромов
- •Свойства синдромов
- •Иллюстрация проверки эквивалентности векторов
- •Синдромный декодер (6, 3)-кода
- •Пример исправления ошибки синдромным декодером
- •Все реализуют принцип максимального правдоподобия
- •Исправляемые конфигурации ошибок
- •Какова вероятность неправильного декодирования?
- •Пример для (6, 3)-кода
- •Вероятность ошибочного декодирования блока (6, 3)-кода
- •Частичное декодирование
- •Пример: Частичное декодирование (6, 3)-кода
- •Вариант частичного декодера
Введение в помехоустойчивое кодирование
|
|
|
|
|
|
|
|
|
Примеры: |
||
|
И |
|
|
К |
|
|
П |
|
|||
|
|
|
|
|
|
• |
Передача данных |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
И - Источник, К - Канал, П - Получатель |
• |
Запись и считывание |
|||||||||
• |
Распознавание ввода |
||||||||||
|
|
|
|
|
|
|
|
|
|||
Повышение достоверности за счет внесения избыточности
И
 КУ
КУ 
 К
К 
 ДКУ
ДКУ 
 П
П
И- Источник, КУ – Кодирующее устройство, К - Канал, ДКУ – декодирующее устройство, П - Получатель

Функциональная схема процесса повышения достоверности
|
x |
|
|
y |
~ |
|
|
|
|
||
|
|
|
y |
|
ˆ |
||||||
|
|
|
|
|
|
|
|
|
|
x |
|
И |
|
|
КУ |
|
|
К |
|
|
ДКУ |
|
П |
|
|
|
|
||||||||
x
y
~
y
xˆ D
- Информационное сообщение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
-Закодированное сообщение
-Возможно искаженное закодированное сообщение
-Оценка информационного сообщения
-Диагностическая информация о результате декодирования: -Не обнаружено искажений -Ошибки обнаружены и исправлены
-Ошибки обнаружены, нет однозначного варианта исправить -Исправлено, мера надежности оценки =… -и.т.п.

Двоичное блоковое кодирование
|
|
|
x |
|
|
|
y |
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|||
|
И |
|
|
|
|
КУ |
|
|
|
К |
|
|
|
|
|
|
ДКУ |
|
|
x |
|
П |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x V |
k |
|
|
y V |
n |
~ |
V |
n |
ˆ |
|
|
k |
||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
x V |
|
|
|
|||||
V {0,1} |
|
- Множество двоичных значений символов |
|
|
|
|
|
||||||||||||||||||
k |
- Число двоичных символов в информационном блоке x |
|
|
|
|||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
||||||||||||||||
- Число двоичных символов в кодовом сообщении y |
|
|
|
n k |
|||||||||||||||||||||
y f (x) |
|
-Функция кодирования (инъективная) |
|
|
|
|
|
|
|||||||||||||||||
x (x1, x2 , xk ) |
y ( y1, y2 , yn ) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x, y - |
|
Двоичные вектора |
|||||||||||||||||||||||
i |
xi V & yi V |
|
|
|
|
|
|
|
|
|
|
|
|
|
размерности k и n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
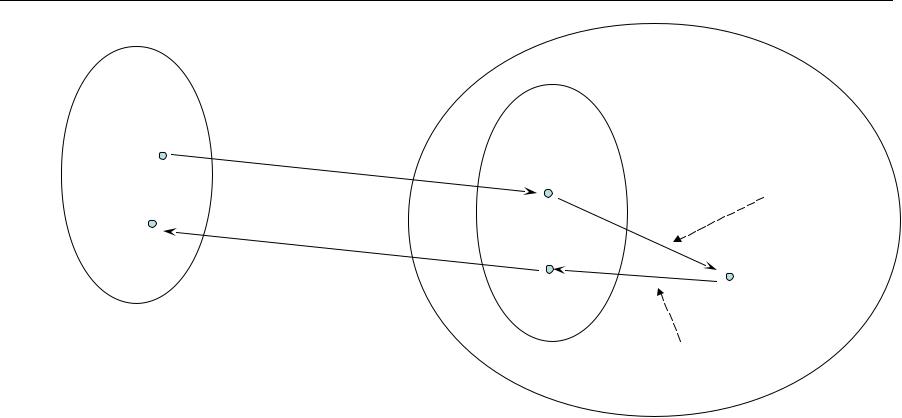
Двоичный блоковый (n, k) код
|
V k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
n |
||||||
|
|
|
|
|
|
|
|
|
Кодирование |
B |
A V |
||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
f |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||||||||
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Искажение |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
f |
1 |
ˆ |
~ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обращение |
|
y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f B(V k ) |
& |
|
|
|
f 1 (V k )B |
|
Оценивание |
||||||||||||||||
B {v | u V k |
f (u) v} -Множество допустимых кодовых векторов (слов) |
||||||||||||||||||||||
B A |
|
B |
|
|
|
|
|
|
V k |
|
|
2k |
|
|
yˆ - Оценка кодового слова |
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
V |
|
|
|
2 |
|
|
|
|
ˆ |
ˆ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Структура декодирующего устройства
~ |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
y |
|
|
ˆ |
|
|
|
|
? |
|
|
f 1 |
x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
Свойство канала |
PК{y | y} |
|
|
|||||
~ |
|
|
|
|
||||
|
Вероятность трансформации кодового вектора y в |
|||||||
|
искаженное сообщение ~ |
|
|
|||||
|
|
|
|
y |
|
Это условная вероятность |
||
Свойство источника PИ{x}
Вероятность того, что информационное сообщение имеет вид x. Это безусловная вероятность
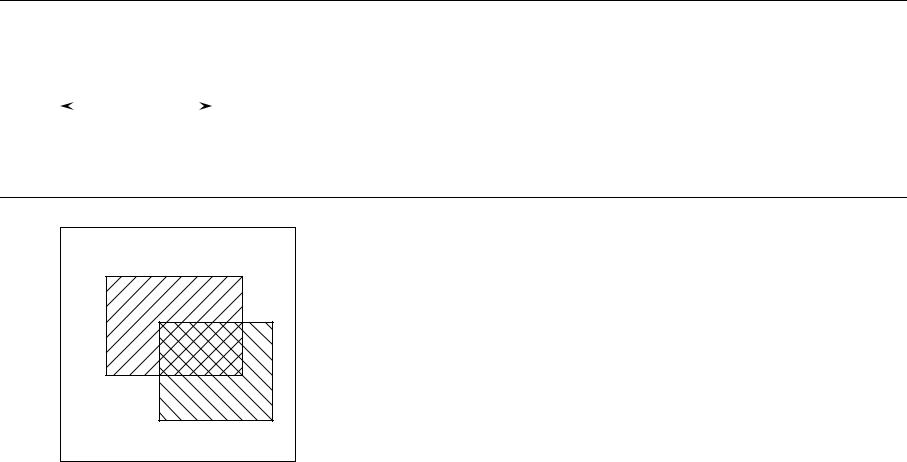
Геометрическая интерпретация вероятности
|
|
A |
|
|
Все попадания во все точки отрезка длины 1 |
|
|
|
|
|
есть равновозможные события. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
p |
1 |
|||
|
|
|
|
|
|
Вероятность события A: попасть в левую |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
часть отрезка длиной p равна P(A)=p/1=p. |
|
|
|
|
|
|
|
Вероятность противоположного события P(~A)=1–P(A)=1–p
A |
AB |
B |
Попадания во все точки квадрата со стороной 1 есть равновозможные события.
Вероятность события A попасть в прямоугольник A площади a P(A)=a/1=a
Вероятность события A попасть в прямоугольник B площади b P(B)=b/1=b
Вероятность события AB попасть в пересечение прямоугольников площадью d P(AB)=d/1=d
Условные вероятности |
|
Независимость A и B |
|
А при условии B: |
P(A|B)=d/b=P(AB)/P(B) |
Если P(A|B)=P(A) |
|
B при условии A: |
P(B|A)=d/a=P(AB)/P(A) |
Тогда P(AB)=P(A)P(B) |
|
Иначе P(AB)=P(A|B)P(B) |
|||
|
|
||
|
|
|
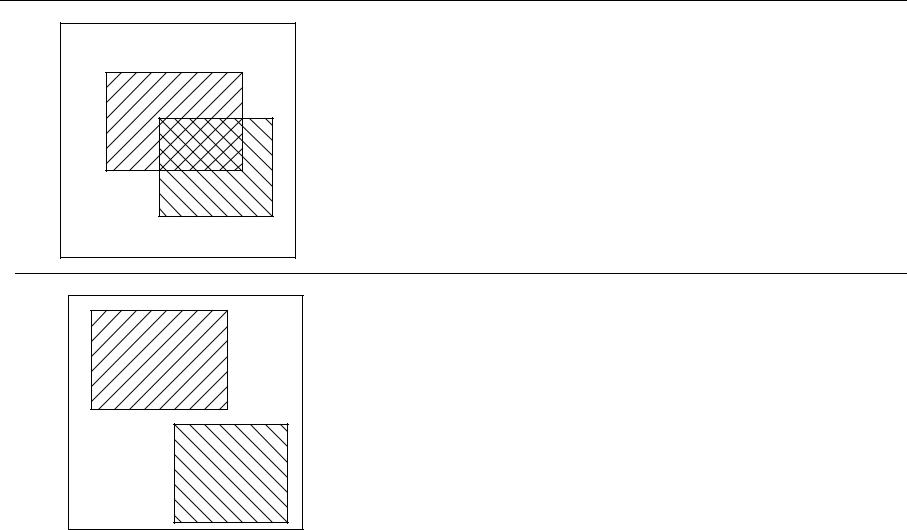
Независимость событий A и B
P(A|B)=P(A): Тогда P(AB)=P(A)P(B) Иначе P(AB)=P(A|B)P(B) Независимость симметрична: P(A|B)=P(A) P(B|A)=P(B)
A |
AB |
B |
P(A)=a P(B)=b P(AB)=d
Вероятность события A+B – попасть в любой из двух прямоугольников
(сумма событий = событие A или B)
P(A+B)=P(A)+P(B)-P(AB)=a+b-d
A |
B |
События A и B несовместны P(AB)=0
Для несовместных событий P(A+B)=P(A)+P(B)
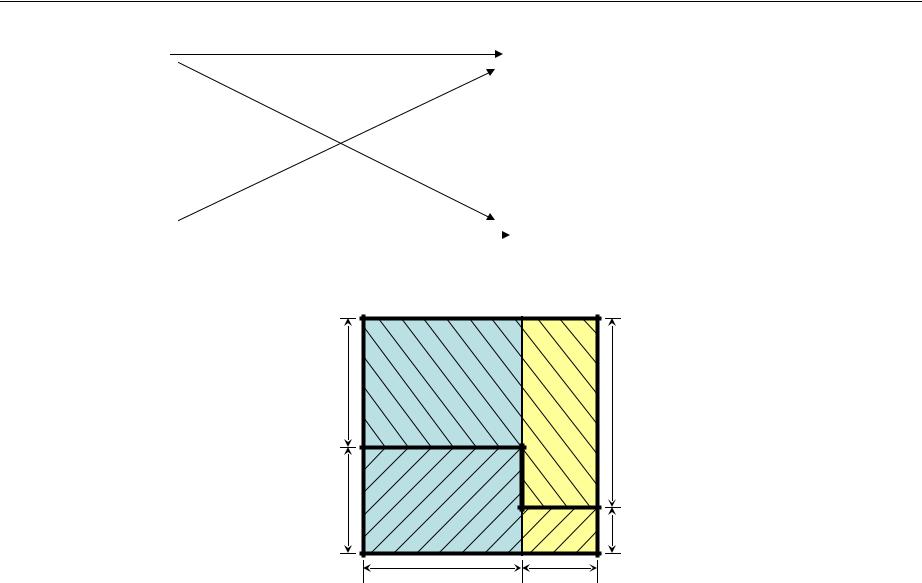
Геометрическая интерпретация формул полной вероятности и формул Байеса для вычисления вероятностей гипотез
P(a)=0,7 |
“a” |
P(c|a)=0,6 |
|
|
|
“c” |
P(c)=0,48 |
|||||
|
|
|
|
,2 |
|
|
P(a|c)=(0,7·0,6)/0,48=0,875 |
|||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
P(b|c)=(0,3·0,2)/0,48=0,125 |
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
P(d)=0,52 |
|
|
|
|
|
|
|
|
=0 |
|
|
||
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
P(d|b)=0,8 |
|
|
|
|
4 |
|
P(a|d)=(0,7·0,4)/0,52=0,538… |
||
P(b)=0,3 |
“b” |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
“d” |
P(b|d)=(0,3·0,8)/0,52=0,462… |
|||
P(c)=0,7·0,6+0,3·0,2=0,48 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
P(d)=0,7·0,4+0,3·0,8=0,52 |
|
|
|
Формулы |
|
P(c)=P(ac)+P(bc) |
P(d|a) |
ad |
|
|
Байеса: |
P(d)=P(ad)+P(bd) |
|
|
P(a|c)=P(ac)/P(c) |
||
|
|
bd |
P(d|b) |
||
P(ac)=P(a)P(c|a) |
|
|
|
|
P(a|d)=P(ad)/P(d) |
P(ad)=P(a)P(d|a) |
P(c|a) |
ac |
bc |
|
P(b|c)=P(bc)/P(c) |
P(bc)=P(b)P(c|b) |
|
|
P(c|b) |
P(b|d)=P(bd)/P(d) |
|
|
|
|
|||
P(bd)=P(b)P(d|b) |
|
P(a) |
P(b) |
|
|

Оценивание по принципу максимального правдоподобия
При известных |
~ |
| y} и |
PИ{x} , какова безусловная вероятность |
|
PК{y |
||||
|
|
|
~ |
|
наблюдать возможно искаженное сообщение y |
? |
|||
~ |
~ |
| f (x)}PИ{x} |
P( y) PК{y |
||
x V k
Формула сложения
вероятностей для 2k несовместных~ гипотез появления y
Какова вероятность, что передавался именно |
x |
~ |
|
(x)}PИ{x} |
|||
ив результате наблюдался |
~ |
|
PК{y | f |
||||
|
|
(События зависимые) |
|||||
y ? |
|
|
|||||
|
|
|
|
|
|
|
|
~ |
|
|
~ |
~ |
|
И |
|
Какова вероятность, что y появился |
|
К |
|
||||
P(x | y) |
P {y |
| f (x )}P {x } |
|||||
именно в результате передачи |
|
|
|
|
|
||
|
|
~ |
| f (x)}PИ{x} |
||||
сообщения x ? |
|
|
|
PК{y |
|||
|
|
|
x V k |
|
|
|
|
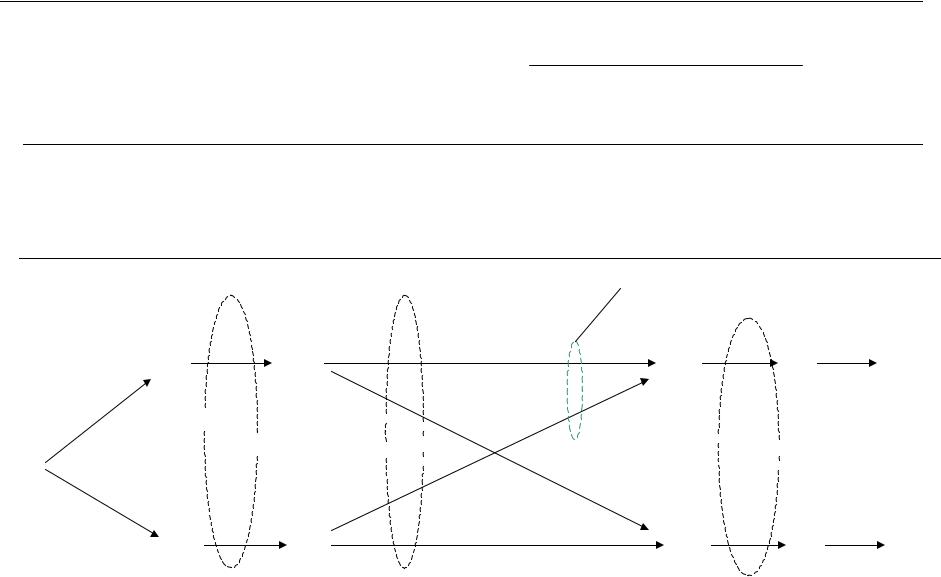
Оценивание по принципу максимального правдоподобия
Какой вариант максимально |
|
|
P {y | f (x)}P {x} |
|
|
|
|
|
||||||||
max |
К |
~ |
ˆ |
|
И |
ˆ |
|
|
|
|
|
|||||
правдоподобный? |
|
~ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
xˆ V k |
|
PК{y | f (x)}PИ{x} |
|
|
|
|
|
|||||
|
|
|
|
|
|
x V k |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
~ |
ˆ |
|
|
1 |
|
|
ˆ |
|
|
max PК{y | |
ˆ |
ˆ |
|
max P {y | y}P { f |
|
( y)} |
||||||||||
|
|
|
К |
|
|
|
И |
|
|
|
|
|
||||
f (x)}PИ{x} |
|
yˆ B |
|
|
|
|
|
|
|
|
||||||
xˆ V k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Выбор гипотезы |
|
|
|
|
|
||||
|
|
f |
|
~ |
| y} |
|
~ |
|
|
f |
1 |
|
||||
|
|
y |
PК{y |
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
y |
|
ˆ |
|
|
|
|
ˆ |
||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
PИ{x} |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
КУ |
K |
|
|
|
PК{y |
| y |
} |
|
|
|
|
|
|
|
И |
|
|
|
|
~ |
|
|
ДКУ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PИ{x } |
|
f |
|
~ |
| y } |
PК{y | y} |
|
|
|
|
f |
1 |
|
|||
x |
y |
P {y |
|
~ |
|
|
yˆ |
|
|
|
|
|||||
|
|
К |
|
|
|
|
|
|
|
|
ˆ |
|||||
|
|
|
|
|
|
y |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
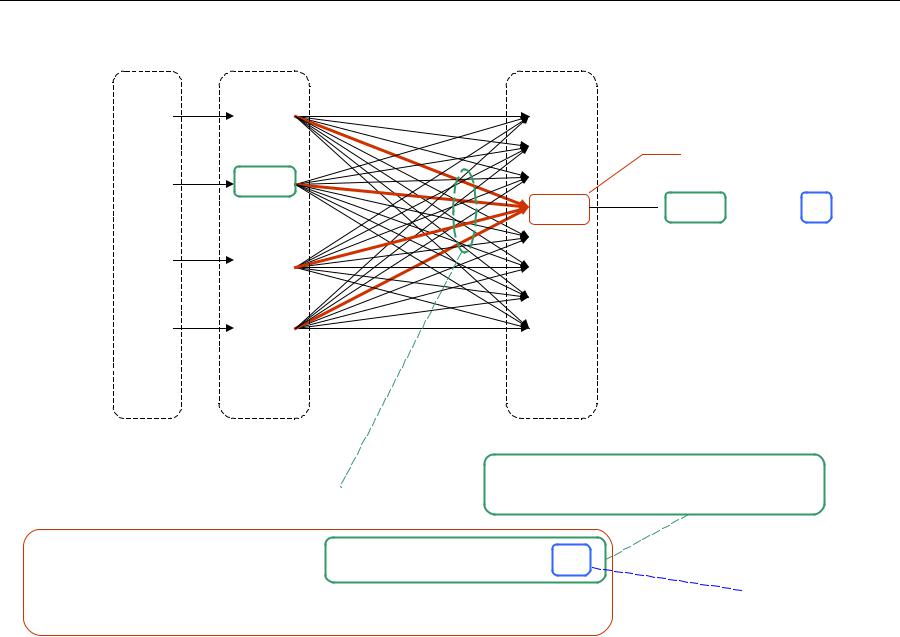
Пример: (3, 2) блоковый двоичный код: n = 3, k = 2.
|
2k 4 |
2n 8 |
|
00 |
000 |
000 |
|
|
|||
|
|
001 |
|
01 |
010 |
010 |
|
|
|
011 |
|
10 |
101 |
100 |
|
101 |
|||
|
|||
|
|
||
11 |
111 |
110 |
|
111 |
|||
|
|
||
V k |
B |
A |
~
А что если 2k слишком большое число?
y
 010
010  01
01
yˆ xˆ
Как реализовать
ˆ ~
x g( y) ?
|
|
~ |
ˆ |
1 |
ˆ |
Выбор одной из 2k гипотез |
max PК{y |
| y}PИ{ f |
|
( y)} |
|
yˆ B |
|
|
|
||
PК{011 | 000}PИ{00} |
PК{011 | 010}PИ{01} |
|
Выход ДКУ |
||
PК{011 |101}PИ{10} |
PК{011 |111}PИ{11} |
|
|||
|
|
|
|||
