Задания по теме «Ряд натуральных чисел. Рекуррентные формулы и функция следования. Принцип индукции. Примеры доказательств в формальной арифметике.»

Используя систему аксиом Пеано для формальной арифметики на множестве натуральных чисел (ℕ) и принцип индукции, докажите следующие свойства арифметических операций + и ·, определяемых рекуррентно:

a+b = b+a

a·b = b·a

a·(b+c) = (a·b)+(a·c)

Определения для операций:

(Правило A) a+1 = s(a)

(Правило B) a+s(b) = s(a+b)

(Правило C) a·1 = a

(Правило D) a·s(b) = (a·b)+a

Определите арифметическую операцию возведения в степень как

(Правило E) a¹ = 1

(Правило F) a^s(b) = a^b·a

и докажите свойства:

a^m+n = a^m·aⁿ

a^m·n = (a^m)ⁿ

Постройте аналогичную систему аксиом и докажите основные свойства арифметических операций для множества ℕ₀ = ℕ  {0} – натуральных чисел с нулем. Для функции следования используйте постфиксную запись при помощи штриха после операнда: x′ обозначает следующий за x элемент ℕ₀.

Указание:

= – инфиксный символ бинарного отношения равенства на ℕ₀ – эквивалентность.

(N1) xℕ₀ x = x

(N2) x = y  y = x

(N3) x = y & y = z  x = z

(N4) x = y    x′ = y′

(N5) 0ℕ₀

(N6)  xℕ₀  x′ = 0

Принцип индукции для ℕ₀:

(N7) ( P(0) & ( xℕ₀ ( P(x) → P(x′) ) ) )  ( xℕ₀ P(x) )

Определения операций:

(Правило А) a+0 = a

(Правило B) a+b′ = (a+b)′

(Правило C) a·0 = 0

(Правило D) a·b′ = (a·b)+a

В системе аксиом для ℕ₀:

- продемонстрируйте применение правил A, B, C, D из указания к предыдущей задаче для вычисления значения выражения 0′′·0′′′;

- представьте правило D только с использованием символов операций ′ и · (исключите символ +). Возможно, для этого вам потребуется вместо правила D ввести два новых правила, чтобы «раскрыть» рекуррентное определение +.

Докажите эквивалентность множеств ℕ и ℕ₀ (найдите взаимно-однозначное соответствие между ними).

Разработайте систему обозначений и набор рекуррентных соотношений для преобразования из «унарной» кодировки чисел множества ℕ₀ в позиционную двоичную запись.

Возможное решение:

Будем числа множества ℕ₀ представлять в виде формул с бинарной операцией, обозначаемой символом ^, играющей роль разделителя разрядов в позиционной двоичной записи, который в общепринятой системе записи обычно опускаются. В данной системе обозначений этот символ показывает, что формула представляет число в двоичной позиционной системе. Правыми операндами этой операции могут быть только значения разрядов позиционной записи.. Левыми операндами – любые формулы, представляющие число в позиционной записи. Фактически эта операция показывает, какое число получится, если к определенной формуле приписать то или иное значение разряда справа.

В двоичной позиционной системе значениями разрядов могут быть только числа 0 и 1. В обозначениях системы аксиом для ℕ₀ эти числа представляются как 0 и 0′ соответственно. Поэтому введем обозначение:

(ДП1): 1=0′.

Для формулировки правил преобразования удобно ввести также специальное обозначение для числа 2:

(ДП2): 2=1′.

Правила перехода от двоичной позиционной системы записи к унарной можно определить следующими соотношениями:

(ДП3): x^0 = x·2,

(ДП4): x^1 = (x·2)+1,

где · обозначает введенную ранее операцию умножения (правила A, B, C, D для + и · в ℕ₀).

Так как левыми операндами могут быть только 0 и 1, последовательным применением правил ДП3 и ДП4 для любой «правильной» формулы с ^ возможно построить эквивалентную ей формулу без ^, включающую только символы 0, 1, 2 и знаки бинарных операций + и ·. Применяя к ней правила A, B, C, D, всегда можно получить представление для числа, использующее единственный символ 0, за которым могут следовать только символы ′, обозначающие применение функции следования требуемое число раз.

Пример: перевод числа одиннадцать из двоичной позиционной в унарную систему записи:

((1^0)^1)^1=((1^0)^1)·2+1=((1^0)·2+1)·2+1=((1·2)·2+1)·2+1=

= ((0′·0′′)·0′′+0′)·0′′+0′ = … = 0′′′′′′′′′′′

Замечание: введенная таким образом операция ^ не является ассоциативной, так как не указано ни одного правила ее вычисления для случая, когда ее правый операнд отличается от 0 и 1. Это вынуждает всегда явно расставлять скобки так, чтобы справа от ^ могли быть только 0 или 1. Для символов ′ в формулах для унарного представления нет необходимости указывать порядок действий скобками, так как последовательно идущие символы ′ фактически представляют применение композиции функции следования в соответствующем числе, а композиции любых функций (одноместных, унарных операций) ассоциативны. Термин «правильная» формула здесь понимается либо 0, либо 1, либо формула с бинарной операцией ^, правыми операндами которой являются только либо 0, либо 1, а левыми операндами – любые формулы.

Для обратного преобразования потребуется задать рекуррентные соотношения и несколько вспомогательных операций. Фактически обратное преобразование моделирует процесс работы цепочки счетных триггеров со сквозным распространением переноса, так как основная задача такого преобразования – счет числа унарных символов. Действительно, если рассматривать входную информацию как последовательность импульсов, которые необходимо сосчитать, то выходная информация может рассматриваться как конечное состояние цепочки двоичных триггеров достаточной для представления результата длины, при условии, что начальное состояние всех счетных триггеров цепочки было нулевым.

Обозначим символом * бинарную операцию, левым операндом которой будет некоторое состояние цепочки двоичных счетчиков (представленное в виде формулы над символами 0 и 1 с бинарной операцией ^ и скобками), а правым операндом – число в «унарной» записи при помощи символа 0, за которым следует произвольное количество символов ′. Пусть результат этой операции символизирует состояние, которое достигнет цепочка счетчиков при обработке импульсов в количестве соответствующих числу символов ′ левого операнда. Зададим правила для вычисления результата операции * рекуррентным соотношением. Для этого удобно ввести еще одну вспомогательную унарную операцию #, применяемую к аналогичной формуле, символизирующей число в двоичной позиционной записи или состояние цепочки счетчиков. Применение этой операции будет показывать, как меняется состояние счетчиков (или формула для двоичной позиционной записи) при увеличении представляемого значения на 1 (или, при обработке единственного счетного импульса). Такую операцию задают следующие рекуррентные формулы:

(СЧ1): 0#=1

(СЧ2): 1#=1^0

(СЧ3): (x^0)#=x^1

(СЧ4): (x^1)#=(x#)^0

Например, то, что в десятичной системе записывается как 11+1=12, в данном представлении будет выглядеть так:

(((1^0)^1)^1)#= ((1^0)^1)#^0=((1^0)#^0)^0=((1^1)^0)^0.

Теперь определим операцию * (тоже рекуррентно):

(СЧ5): x*0=x

(СЧ6): x*y′=x#*y

Тогда функция g преобразования числа из унарной в двоичную позиционную запись может быть представлена в виде

(СЧ7): g(x)=0*x

Пример преобразования числа 5 из унарной в двоичную позиционную запись:

g(0′′′′′)=0*0′′′′′=0#*0′′′′=1*0′′′′=1#*0′′′=(1^0)*0′′′=(1^0)#*0′′=(1^1)*0′′=

=(1^1)#*0′=(1#^0)*0′=((1^0)^0)*0′=((1^0)^0)#*0=((1^0)^1)*0=(1^0)^1

Можно построить аналогичную систему правил, не используя символ #, комбинируя правила СЧ5, СЧ6 и правила СЧ1, СЧ2, СЧ3, СЧ4:

(A0): (x)*0=x

(A1): 0*x′=1*x

(A2): 1*x′=(1^0)*x

(A3): (x^0)*y′=(x^1)*y

(A4): (x^1)*y′=((x*0′)^0)*y

(A5): g(x)=0*x

В таких обозначения только что рассмотренное преобразование будет выглядеть так:

g(0′′′′′)=0*0′′′′′=1*0′′′′=(1^0)*0′′′=(1^1)*0′′=((1*0′)^0)*0′=

=(((1^0)*0)^0)*0′=((1^0)^0)*0′=((1^0)^1)*0=(1^0)^1

Аналогично тому, как была показана несчетность множества бесконечных двоичных последовательностей ℬ^ℕ, покажите несчетность множества троичных бесконечных последовательностей A^ℕ для некоторого A={a, b, c}.

Указание. Постройте какую-либо инъективную функцию f из A в A, для которой выполняется условие: xA f(x)x и используйте ее аналогично бинарному отрицанию  для построения незанумерованной последовательности.

Установите, какие из следующих бинарных отношений, заданных различными способами, являются отношениями эквивалентности:

1. A = {a, b, c, d, e}

 = {(a, a), (b, b), (c, c), (d, d), (e, e), (a, b), (b, a),

(b, c), (c, b), (a, c), (c, a), (d, e), (e, d), };

2. A = {a, b, c, d, e}

3. A = {a, b, c, d, e}, a₁=a, a₂=b, a₃=c, a₄=d, a₅=e

.

Отношения порядка.

Рассмотрите отношение делимости целых чисел от 1 до 20. Пусть множество этих чисел обозначено как A={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20}, а бинарное отношение делимости AA. ={(x, y)| xA & yA & xy}.

Здесь «» – инфиксный символ для обозначения делимости. Читается «x делит y». Постройте диаграмму Хассе простых отрезков этого отношения, а по ней восстановите само отношение, представив его списком упорядоченных пар и матрицей.

Начать удобнее снизу: число 1 делит все остальные, поэтому по диаграмме из узла 1 все узлы достижимы. Простыми отрезками узел 1 соединяется только с простыми числами этого диапазона. Условие для простого отрезка с нижней границей 1 для отношения делимости выглядит так:

[1, b]_ ={x | (1x) & (xb)}  ([1, b]_={1, b}  x (xb  ((x=1)  (x=b))))

Поэтому условие [1, b]_={1, b} означает, что b – простое число.

Таким образом, с 1 простыми отрезками связаны числа 2, 3, 5, 7, 11, 13, 17, 19. Выпишем их во втором снизу «слое» диаграммы. Следующий слой составят числа, делящиеся только на перечисленные простые числа (а также на себя и на 1). Это будут числа 4=2·2, 6=2·3, 9=3·3, 10=2·5, 14=2·7, 15=3·5. Далее идут числа, делящиеся на эти и на лежащие ниже по диаграмме: 8=4·2, 12=4·3=6·2, 18=6·3=9·2, 20=4·5=10·2. На самом верху будет число 16, единственное, делящиеся на числа четвертого слоя: 16=8·2.

Соединим на диаграмме числа из верхнего слоя с теми из нижнего, на которые оно делится. Получим следующую диаграмму:

Вообще-то она направленная (снизу вверх), но при изображении таких диаграмм можно направленность связей не указывать, так как она известна. Отмеченные связи будут как раз простыми отрезками отношения делимости. На данной диаграмме наглядно иллюстрируется понятие внутренней точки отрезка: это узлы, лежащие на пути из нижней в верхнюю границу отрезка. Например, для отрезка [3,18] внутренними точками будут числа 6 и 9:

[3, 18]_ = {3, 6, 9, 18}

Построим теперь список пар самого отношения делимости. Для каждого числа числами, которое оно делит будут оно само и все числа, достижимые из него при движении вверх по диаграмме.

 = {{1,1}, {1,2}, {1,3}, {1,4}, {1,5}, {1,6}, {1,7}, {1,8}, {1,9}, {1,10}, {1,11},

{1,12}, {1,13}, {1,14}, {1,15}, {1,17}, {1,18}, {1,19}, {1,19}, {1,20},

{2,2}, {2,4}, {2,6}, {2,8}, {2,10}, {2,12}, {2,14}, {2,16}, {2,18}, {2,20},

{3,3}, {3,6}, {3,9}, {3,12}, {3,15}, {3,18}

{4,4}, {4,8}, {4,12}, {4,16}

{5,5}, {5,10}, {5,15}, {5,20}

{6,6}, {6,12}, {6,18}

{7,7}, {7,14}

{8,8}, {8,16}

{9,9}, {9,18}

{10,10}, {10,20}

{11,11}, {12,12}, {13,13}, {14,14}, {15,15},

{16,16}, {17,17}, {18,18}, {19,19}, {20,20}}

Матрица этого отношения при нумерации элементов по их числовым значениям будет такой (отмечены только единичные значения, нулевые опущены):

От строки к строке расстояние межу единицами по горизонтали увеличивается на одну позицию от 1 до 20.

Назовем пару двоичных векторов некоторой размерности упорядоченными, если первый из них своими единичными значениями является подмножеством среди единичных компонентов второго. То есть для вектора X=(x₁, x₂,…x_n) при условии k x_k{0, 1} имеется множество индексов его единичных компонент: I_X={k | x_k=1}. Аналогично Y=(y₁, y₂,…y_n), k y_k{0, 1} и I_Y={k | y_k=1}. Тогда определим отношение ≼ как

X≼Y  I_X  I_Y

Покажите, что X≼Y  k x_k→y_k и что отношение ≼ является частичным порядком для n>1. Постройте диаграмму Хассе и матрицу для этого отношения для случая n=4.

Назовем расстоянием между такими векторами число позиций, в которых они различаются. Функцию от двух векторов, вычисляющую число различий, обозначим символом d:

(сумма числа позиций, где вектора различаются)

Покажите, что d(X, Y)=|I_X∸I_Y| (число элементов в симметрической разности множеств индексов единичных компонентов векторов). Пользуясь построенной диаграммой объясните, почему расстояние между границами простых отрезков равно 1:

([X, Y]_≼ = {X, Y})  d(X, Y)≤1

Для простого графа, заданного множествами вершин и ребер

1. Изобразите диаграмму;

2. Постройте матрицу смежности;

3. Постройте матрицу инцидентности;

4. Для каждой вершины укажите множество смежных вершин;

5. Для каждой вершины укажите ее степень.

Указания:

1. Для матриц смежности необходимо выбрать нумерацию вершин;

2. Для матриц инцидентности необходимо указать нумерацию вершин и нумерацию ребер.

Варианты графов:

1) V={a, b, c, d, e, f, g}

E={{a, b}, {c, f}, {d, b}, {a, e}, {e, c}, {a, b}, {g, c}}

2) V={1, 2, 3, 4, 5, 6, 7, 8}

E={{1, 2}, {4, 6}, {3, 2}, {7, 3}, {2, 8}, {1, 7}, {3, 4}}

3) V={1, 2, 3, 4, 5, 6, 7, 8}

E={{1, 3}, {5, 6}, {3, 7}, {5, 8}, {2, 8}, {1, 7}, {3, 5}}

4) V={a, b, c, d, e, f, g}

E={p, q, r, s, t, u}

p={a, c}, q={d, f}, r={a, f}, s={b, e}, t={d, f}, u={a, g}

Для известной матрицы инцидентности некоторого простого графа найдите его матрицу смежности. Изобразите диаграмму для этого графа. Узлы диаграммы обозначьте номерами вершин.

Варианты матриц инцидентности:

1)

2)

Для известной матрицы смежности некоторого простого графа найдите его матрицу инцидентности, введя некоторую нумерацию ребер. Изобразите диаграмму для этого графа. Узлы диаграммы обозначьте номерами вершин.

Варианты матриц смежности:

1)

2)

Для простого графа, заданного диаграммой, постройте матрицу смежности и матрицу инцидентности, используя числа в узлах диаграммы как номера вершин, а числа у линий диаграммы как номера ребер.

Модифицируйте процедуру вычисления маршрутов минимального веса по алгоритму Флойда-Уоршала так, чтобы вместо числовых значений весов ребер использовалось логические значения отношения смежности вершин:

и результатом работы алгоритма была бы матрица отношения связности данного графа. Чем в данном случае должны быть:

0 – минимальное значение веса ребра

(в этом примере обозначенное курсивом 0, чтобы отличать его от логически ложного значения 0);

 – максимальное значение веса ребра;

+ – операция сложения значений весов ребер;

 – отношение упорядоченности значений весов ребер;

min – операция выбора минимального значения из двух весов ребер?

Указание:

0 = 1 – логически истинное значение: вершины смежные.

 = 0 – логически ложное значение: вершины не смежные.

+ – операция ЛОГИЧЕСКОЕ И:

(a, b, c) маршрут  {a, b}E & {b, c}E :

x + y = x & y .

 – Есть всего два значения: 0 и . Список их допустимых комбинаций в отношении  следующий:

00, 0, .

С учетом того, что это логические значения 0 и 1, имеем

11=1, 10=1, 00=1, 01=0

или, в виде таблицы:

Это бинарная логическая операция является импликацией с обратным порядком операндов, ранее обозначенная символом  :

x  y = x  y .

min – Есть всего два значения: 0 и  со следующими правилами вычисления результата бинарной операции min:

min(0, 0)=0, min(0, )=0, min(, 0)=0, min(, )=.

С учетом того, что это логические значения 0 и 1, имеем:

min(1, 1)=1, min(1, 0)=1, min(0, 1)=1, min(0, 0)=0,

или, в виде таблицы:

Это бинарная операция ЛОГИЧЕСКОЕ ИЛИ, обозначаемая символом :

min(x, y) = x  y .

Тогда шаг алгоритма может быть записаны в виде:

.

Пользуясь полученным представлением, напишите программу на любом удобном для вас языке программирования, реализующую вычисление матрицы достижимости для некоторого бинарного отношения по данному алгоритму.

Замечание: произвольное бинарное отношение представляется ориентированным графом, поэтому представляющая его матрица в общем случае не симметричная, но к ней также применим рассмотренный алгоритм.

Представьте все возможные бинарные (двухместные) логические операции в виде двумерных таблиц (таблицы Кэли). Установите, какие из них обладают рассмотренными специальными элементами: левыми и правыми нейтральными, левыми и правыми нулевыми.

Например:

	Нет нейтральных и нулевых элементов
	Два левых нейтральных: 0 и 1, правых нет. Два правых нулевых: 0 и 1, левых нет.

Установите, какие из бинарных логических операций ассоциативны.

Указание: достаточно рассмотреть только по одной из операций из каждого из изученных классов эквивалентности по изоморфизму. Для доказательства ассоциативности следует вычислить и сравнить на равенство выражения (ab)c и a(bc) для всех 8 возможных комбинаций значений операндов a, b, c. Для опровержения ассоциативности достаточно привести одно сочетание таких значений, например:

a	b	c	(ab)c	a(bc)
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	0
1	0	0	1	1
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

 — ассоциативная операция.

→ — не ассоциативная операция.

Так как ручная проверка ассоциативности перебором всех комбинаций операндов трудоемкая, имеет смысл подумать об автоматизации получении решения при помощи написания соответствующих программ.

На некотором трехэлементном множестве бинарную операцию можно ввести 3⁹=19683 способами. Попробуйте при помощи подходящей программы установить, на сколько классов по отношению изоморфизма они разбиваются.

Указание: на трехэлементном множестве кроме тождественной функции вида существуют еще 5 биективных функции (перестановки трех символов).

Эти функции для множества {a, b, c} можно представить следующей таблицей:

x	f1(x)	f2(x)	f3(x)	f4(x)	f5(x)
a	a	c	b	b	c
b	c	b	a	c	a
c	b	a	c	a	b

Так как изоморфными, но отличными от некоторой алгебры могут быть только получаемые из данной алгебры заменой обозначений операндов по каждой из 5 функций, следует как-либо упорядочить перечисление всех алгебр, например так:

Алгебру на множестве A={a, b, c} представим строкой из 9 символов, где каждый из символов в строке это либо a либо b либо c. Такая строка, например, может представлять выписанные подряд три строки таблицы Кэли некоторой алгебры. Тогда упорядочим (и занумеруем) алгебры аналогично тому, как в словарях слова выстраивают в алфавитном порядке:

Номер алгебры	Cтрока, представляющая алгебру	Таблица Кэли
1	aaaaaaaaa
2	aaaaaaaab
19683	ccccccccc

Вам потребуются процедуры для перевода номера алгебры в строку и обратно, а также процедура получения строки алгебры, при замене символов в ней согласно каждой из 5 схем перестановок обозначений символов. Строки, представляющие алгебры, можно рассматривать как номера алгебр, начинающиеся от 0 в троичной записи, где символ a обозначает цифру 0, символ b – цифру 1, а символ c – цифру 2. Тогда, например, алгебра №11783 будет представлена так:

11783=1·3⁸+2·3⁷+1·3⁶+1·3⁴+1·3³+1·3²+1·3¹=12101110₍₃₎=bcbabbbba

Ей соответствует таблица

Найдем алгебру (одну из изоморфных к ней), соответствующую, например применению функции f₂ и упорядочим строки и столбцы таблицы в алфавитном порядке символов:

⇨ ⇨

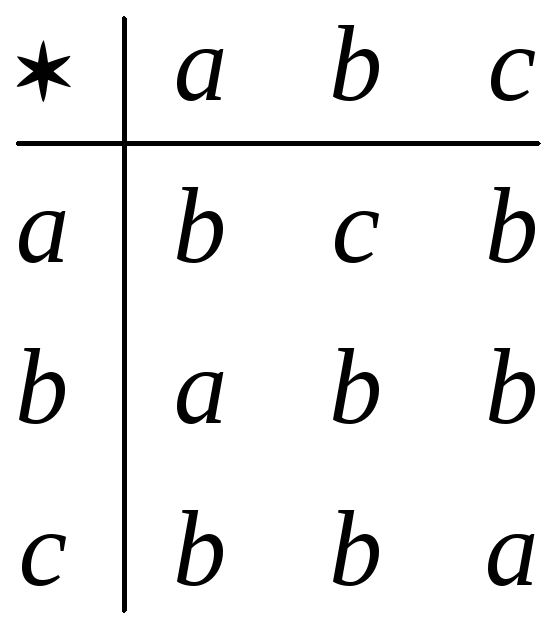Такой алгебре соответствует строка cbbbbcbab, которая имеет номер:

cbbbbcbab=211112101₍₃₎= 2·3⁸+1·3⁷+1·3⁶+1·3⁵+1·3⁴+2·3³+1·3²+1·3⁰=16428.

Тогда программа для установления числа классов трехэлементных алгебр могла бы следовать примерно следующему алгоритму:

1. Заполняем список из 19683 двоичных признаков (битов) логически истинными значениями.

2. Ищем наименьший по номеру (от 0 до 19682) элемент списка с логически истинным значением (единичный бит в строке из 19683 битов). На начальном этапе это будет элемент №0.

3. Заменяем значение признака с этим номером на логически ложное (нулевое значение бита в строке).

4. Строим строку (троичное число), представляющую алгебру с данным номером.

5. Для каждой из 5 биективных функций строим строку, представляющую изоморфную алгебру и для нее:

1. Вычисляем номер этой изоморфной алгебры: переводим троичное число из троичной записи в номер элемента-признака (номер бита).

2. Заменяем значение признака с этим номером на логически ложное (нулевое значение бита в строке).

6. Проверяем, остались ли еще логически истинные признаки в списке. Если да, то переходим к повторению пункта (2), иначе процедура заканчивается.

Число выполненных итераций будет равно числу классов трехэлементных алгебр, так как на каждой итерации из списка удаляются все алгебры, изоморфные выбранному представителю класса с наименьшим номером.

Покажите, что в любом моноиде множество обратимых слева элементов замкнуто относительно бинарной операции .

Докажите, что алгебраическую группу можно определить в такой форме:

Если – алгебра с ассоциативной операцией (a b c (ab)c = a(bc)) и любой элемент можно выразить через любой в левой и правой форме:

то такая алгебра является группой.

Указание: сначала покажите наличие в такой алгебре левого и правого нейтральных элементов, применяя определяющее свойство к одному элементу, например, наличие левого нейтрального элемента покажите, доказав следующее утверждение:

Т.е. то, что некоторый u «подходит» в качестве левого нейтрального некоторому x, то он же (u) «подойдет» и любому y. При этом обратите внимание, что y тоже можно выразить через x: y=xz.

Постройте таблицу сложения целых чисел {0, 1, 2, 3} по модулю 4 и таблицу умножения целых чисел {1, 2, 3, 4} по модулю 5. Покажите, что эти алгебры изоморфны и обе являются циклическими группами из 4 элементов.

Постройте таблицу сложения классов вычетов целых чисел по модулю 8. Покажите, что это циклическая группа и найдите все ее образующие элементы.

Рассмотрите алгебру композиций перестановок трех символов a, b, c (включая пустую), всего, таким образом имеются 6 перестановок. Опишем схемы таких перестановок в терминах номеров переставляемых позиций:

Номер перестановки	Схема	Описание перестановки
0		Пустая перестановка: все элементы сохраняют свои позиции.
1		Второй и третий элементы меняются местами
2		Первый и второй элемент меняются местами
3		Первый и второй элемент меняются местами
4		Циклическая перестановка со сдвигом вправо
5		Циклическая перестановка со сдвигом влево

Назовем результатом композиции двух перестановок одну из перечисленных перестановок, эквивалентную последовательному применению двух исходных. Например, следующий рисунок показывает, что перестановка №5 является композицией перестановок №1 и №2:

Обозначим все множество возможных перестановок как A={0, 1, 2, 3, 4, 5, 6}, а бинарную операцию их композиции символом . В соответствии с рассмотренным примером будем записывать 12=5.

Обратите внимание, что это некоммутативная операция, так как непосредственным построением диаграммы для выражения 21 можно убедится, что 21412 :

Постройте полную таблицу всех возможных композиций таких перестановок. Рассматривайте ее как таблицу Кэли некоторой алгебры :

Покажите, что данная алгебра является некоммутативной алгебраической группой из шести элементов.

Найдите ее нейтральный элемент.

Для каждого элемента найдите его единственный двусторонне-обратный.

Для каждого элемента найдите порождаемую им циклическую подгруппу.

Для каждой такой подгруппы постройте семейства левых и правых смежных классов, порождаемых каждым элементом. Убедитесь, что каждое такое семейство образует разбиение множества A на непересекающиеся подмножества.

Рассмотрите алгебру композиций поворотов квадрата с вершинами, обозначенными символами a, b, c, d, вокруг его осей симметрии, переводящих его в себя по следующим схемам:

Номер	Схема	Описание
0		Поворот вокруг центра на 360°
1		Поворот вокруг центра по часовой стрелке на 90°.
2		Поворот вокруг центра по часовой стрелке на 180°.
3		Поворот вокруг центра по часовой стрелке на 270°.
4		Поворот вокруг вертикальной оси на 180°.
5		Поворот вокруг горизонтальной оси на 180°.
6		Поворот на 180° вокруг диагонали, проведенной из левого верхнего в правый нижний угол .
7		Поворот на 180° вокруг диагонали, проведенной из правого верхнего в левый нижний угол.

Пример: композиция поворотов №2 и №6 эквивалентна одиночному повороту №7. Следующий рисунок поясняет это.

Обозначьте множество всех рассмотренных поворотов как A={0, 1, 2, 3, 3, 4, 5, 6, 7}, а операцию их композиции символом . Постройте таблицу Кэли для алгебры этих композиций . Покажите, что это нециклическая группа из 8 элементов. Для каждого элемента найдите его обратный. Найдите все собственные подгруппы данной группы.

Для множества всех двоичных векторов размерности 3 найдите расстояния Хэмминга для всех возможных пар векторов. Оформите результат в виде квадратной таблицы.

Источник может порождать два вида сообщений: 0 и 1. Кодирующее устройство в качестве функции кодирования использует трехкратное повторение символа, порожденного источником. В обозначениях, использованных при рассмотрении примера с двоичными кодами такая схема выглядит следующим образом:

Размер информационного блока k=1.

Размер закодированного сообщения n=3.

Множество информационных векторов V^k={0, 1}.

Множество допустимых кодовых векторов B={000, 111}.

Функция кодирования f(0)=000, f(1)=111.

Укажите, какой из двух допустимых векторов множества B следует принять как максимально правдоподобную оценку для каждого из возможных результатов наблюдаемых искаженных сообщений из множества A={000, 001, 010, 011, 100, 101, 110, 111}.

Для принятого правила написания цифр почтового индекса

рассмотрите сочетания закраски линий как значения двоичных векторов из девяти компонентов y=(y₁, y₂, y₃, y₃, y₄, y₅, y₆, y₇, y₈, y₉), где значение компонента 1 означает закрашенный сегмент, а значение 0 – не закрашенный. Тогда можно считать, что правильно написанные цифры образуют множество допустимых кодов среди всех возможных значений двоичных векторов размерности 9. Эти значения можно свести в следующую таблицу:

Обозначаемая цифра	Номера компонентов вектора y
	1	2	3	4	5	6	7	8	9
0	1	1	0	1	0	1	0	1	1
1	0	0	1	1	0	0	0	1	0
2	1	0	0	1	0	0	1	0	1
3	1	0	1	0	1	0	1	0	0
4	0	1	0	1	1	0	0	1	0
5	1	1	0	0	1	0	0	1	1
6	0	0	1	0	1	1	0	1	1
7	1	0	1	0	0	1	0	0	0
8	1	1	0	1	1	1	0	1	1
9	1	1	0	1	1	0	1	0	0

Постройте таблицу расстояний Хэмминга между данными кодами.

Считая, что устройство для сортировки писем использует оптический сканер, на выходе которого для каждой позиции шаблона имеется двоичное значение 1 при условии, что соответствующая позиция закрашена и 0 в противном случае, найдите для приведенных далее вариантов закраски шаблона, какая будет вынесена решающим устройством оценка значения цифры, полагая что решения выносятся согласно принципа декодирования по минимуму расстояния.

Замечание: если имеется несколько максимально правдоподобных решений, укажите их все в виде множества.

Источник порождает сообщения блоками по 2 двоичных разряда. Кодирующее устройство отображает их в кодовые вектора, повторяя каждый из символов три раза. Покажите, что данная схема кодирования соответствует систематическому матричному коду и найдите его кодирующую матрицу. Найдите множество допустимых кодов, расстояния Хэмминга между ними и веса всех ненулевых допустимых кодов.

Для двоичного группового кода, порождаемого матрицей по функции кодирования найдите подгруппу допустимых кодовых векторов B и семейство смежных классов . Образующими векторами смежных классов выбирайте вектора минимально возможных весов (для данного кода выбор не всегда однозначен). Постройте проверочную матрицу этого кода и для каждого смежного класса укажите значение вектора синдрома.

Постройте таблицы Кэли для сложения и умножения целых чисел из множества A={0, 1, 2, 3, 4} по модулю 5. Рассмотрите эти таблицы как поле . Для каждого элемента данной алгебры укажите:

Множество всех значений кратных элементов (степеней по +).

Множество всех значений степеней по операции ·.

Обратный элемент по операции +.

Обратный элемент по операции ·, если он есть.

Покажите, что группа «умножения» ненулевых элементов – циклическая (укажите ее образующий элемент).

Используя свойство неразложимости на собственные сомножители многочлена с коэффициентами из поля с двумя элементами , A={0, 1}, постройте таблицу «умножения» для поля из 8 элементов, как таблицу умножения классов вычетов F[A] по модулю . Каждый класс обозначьте либо многочленом степени не более 2 вида , либо двоичным вектором из трех компонентов .

Для поля из трех элементов, A={0, 1, 2} (оно изоморфно сложению и умножению классов вычетов целых чисел по модулю 3) найдите неразложимый на собственные сомножители многочлен степени 2 из F[A] и с его помощью постройте таблицу «умножения» для поля из девяти элементов. Покажите, что в этом случае группа «умножения» ненулевых элементов (их 8) будет циклической. Укажите ее образующие элементы.

Используя предпочитаемый вами язык программирования реализуйте процедуры умножения и деления с остатком для многочленов с коэффициентами из поля двух элементов , A={0, 1}. Многочлены следует по возможности представлять значениями двоичных разрядов некоторого типа данных, над которым удобно выполнять поразрядную операцию ИСКЛЮЧАЮЩЕЕ ИЛИ и сдвиг влево для представления умножения на одночлен X^k. В языке C это может быть целый беззнаковый тип unsigned int, например, представляющий 32-битные значения. Для начала считайте, что максимальная степень многочлена укладывается в число разрядов такого типа. Затем попробуйте найти обобщение вашей программы для многочленов большей степени. Для языка Pascal рассмотрите возможность использовать тип-множество (set of), эффективно представляющий операции над битовыми строками из нескольких слов.

BS

1