Еще о формулах с кванторами

Формула, отражающая, что некоторое свойство P выполняется только для одного объекта в предметной области, записывается так:

!x P(x)

Читается «Существует единственный x такой, что P(x)». Это сложное высказывание, его проще понять как состоящее из двух:

1.Утверждение, что объект с данным свойством существует.

2.Утверждение о единственности такого объекта.

!x P(x) = ( x P(x)) & ( x y ( P(x) & P(y) ) → (x=y) )

Используемые сокращения

x A (x) для формулы x ((x A) → (x))

x A (x) для формулы x ((x A) & (x))

!x A (x) для формулы !x ((x A) & (x))

Функциональные отношения

(функции между множествами)

BA = { f | f A B & ( x A ! y B (x, y) f )}

y = f(x) (x, y) f

Представление функций ориентированными графами

Здесь A = { a, b, c }, B = { p, q, r, s }, f = { (a, p), (b, p), (c, r) }, f B

классификационные признаки, вводимые для функций:

•Функция f BA называется сюръективной, если

y B x A y = f(x). В этом случае множество B полностью покрыто значениями функции.

•Функция f BA называется инъективной, если разным аргументам она ставит в соответствие разные результаты. По иному это можно сформулировать так: из равенства результатов логически следует равенство аргументов: ( f(x)=f(y) ) ( x=y ).

В определении инъективной функции, таким образом, полагается заданным равенство на обоих множествах, A и B.

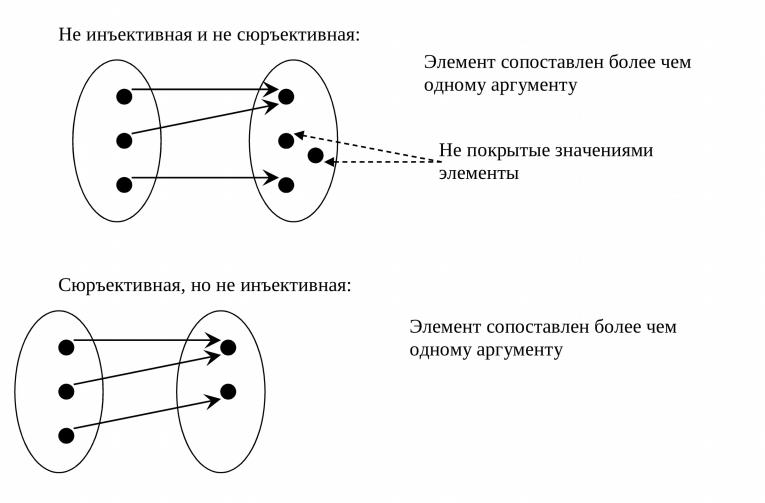
Примеры наличия/отсутствия признаков у функции

Взаимно-однозначные соответствия

Функция, являющаяся одновременно инъективной и сюръективной, называется

биективной.

Биективная функция f BA устанавливает

взаимнооднозначное соответствие между множествами А и B:

( x A !y B (x, y) f ) & ( y B ! x A (x, y) f ).

Сюръективная функция существует тогда и только тогда, когда в A элементов больше или равно, чем в B.

Инъективная функция существует тогда и только тогда, когда в B элементов больше или равно, чем в А.

Биективная функция существует тогда и только тогда, когда число элементов во множествах A и B совпадает.

Обращение функции

( f BA & f -1 AB ) ( x A !y B (x, y) f ) & ( y B !

x A (x, y) f )

Множества А и B называют эквивалентными или равномощными, если между ними можно установить взаимнооднозначное соответствие

A~B ( f BA ( f -1 AB ))