
Шапкарин Лабораторный практикум по курсу 2007
.pdf
W (s) = |
|
KT1 |
|
|
1 |
|
+ |
|
KT2 |
|
|
1 |
, |
||
T |
|
|
T s +1 |
T |
|
|
T s +1 |
||||||||
|
|
−T |
|
|
|
−T |
|
|
|||||||
|
1 |
|
2 |
|
1 |
|
|
2 |
|
1 |
|
2 |
|
||
где коэффициенты перед дробями являются вычетами передаточной функции, вычисленными в соответствующих полюсах. Получаем представление передаточной функции в виде параллельного соединения двух апериодических звеньев, как показано на рис. 3.1.
K |
1 |
T1 −T2 |
s |
u |
1 |
|
y1 |
|||
|
y |
|||||
|
|
T1 |
||||
|
|
|
|
|
||
|
K |
1 |
|
y2 |
||
|
|
|
||||
|
T2 −T1 |
|
|
s |
|
|
|
|
1 |
|
|
||
|
|
|
T2 |
|
|
|
Рис. 3.1
Реакция на ступенчатое входное воздействие системы представляет собой сумму реакций апериодических звеньев, находящихся в параллельных ветвях соединения:
|
KT |
|
|
− |
t |
|
|
KT |
|
|
− |
t |
|
||
|
|
T |
|
|
T |
||||||||||
h(t) = |
|
1 |
|
1 − e |
1 |
|
+ |
|
2 |
|
1 − e |
2 |
|
||
|
|
|
|
|
|
|
|
|
. |
||||||
T |
−T |
|
|
T |
−T |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
2 |
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
Упрощая последнее выражение, получим
|
|
|
|
|
T |
|
−T |
|
|
T |
|
−T |
|
||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
t |
|
h(t) = K |
|
− |
|
1 |
e |
1 |
+ |
|
2 |
e |
2 |
||||
1 |
|
|
|
|
|
|
|
|
|
. |
|||||
T |
−T |
|
|
T |
−T |
|
|
||||||||
|
|
|
|
1 |
2 |
|
|
|
2 |
1 |
|
|
|
|
|
На рис. 3.2 представлены графики переходных процессов в параллельных ветвях и их сумма для случая T1 > T2.
Из рисунка видно, что суммарный график h(t) имеет точку перегиба и представляет собой монотонно возрастающую функцию от нуля до установившегося значения, равного коэффициенту усиления K. Отметим, что в начальный момент времени не только выходной
41
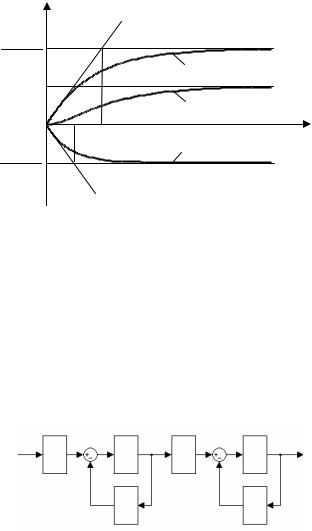
сигнал равен нулю, но и его первая производная по времени также равна нулю, поскольку наклоны касательных в нуле к переходным характеристикам в ветвях параллельного соединения одинаковые по величине и противоположные по знаку. Это соответствует принятому соглашению о нулевых начальных условиях по умолчанию.
h(t) |
|
|
|
KT1 |
|
|
|
T1 −T2 |
|
|
h1 |
K |
|
|
h |
|
|
|
|
0 |
T2 |
T1 |
t |
|
|||
KT2 |
|
|
h2 |
|
|
|
|
T2 −T1 |
|
|
|
|
|
|
Рис. 3.2 |
Структурная модель в виде последовательного соединения
Для получения логарифмических частотных характеристик удобно использовать метод разбиения передаточной функции на простые множители, что означает представление ее в виде произведения типовых динамических звеньев. Именно в виде произведения двух апериодических звеньев и задана передаточная функция системы в рассматриваемом примере. Таким образом, структурная модель принимает вид последовательного соединения двух апериодических звеньев на рис. 3.3, причем не имеет значения порядок их соединения.
u K |
1 |
|
1 |
1 |
y |
|||
|
T1 |
|
s |
T2 |
|
s |
|
|
|
|
1 |
|
|
1 |
|
||
|
|
|
T1 |
|
|
|
T2 |
|
Рис. 3.3
42
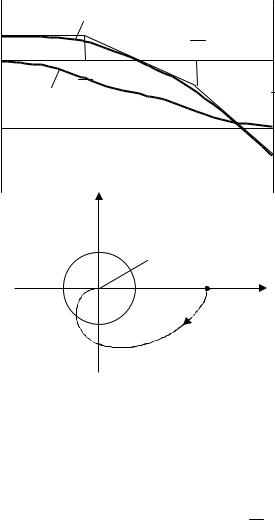
Логарифмические амплитудную и фазовую частотные характеристики последовательного соединения получают путем суммирования соответственно амплитуд и фаз всех элементов соединения.
Результирующие ЛАФЧХ и годограф передаточной функции для рассматриваемого примера приведены на рис. 3.4, а и б.
|
L, дБ |
L(ω) |
|
|
θ, град |
|
20lgK |
-20 |
1 |
|
|
|
T2 |
|
|
||
|
0 |
|
0 |
||
|
1 |
|
|
||
|
|
|
|
|
|
а) |
θ(ω) |
T1 |
|
-40 |
-90 |
|
|
|
|
|
|
|
-40 |
|
|
|
-180 |
|
Im |
пл. W ( jω) |
|
|
|
|
|
|
ω →∞ |
|
|
б) |
|
ω = |
0 |
|
|
|
|
-1 |
1 |
K |
Re |
Рис. 3.4 |
|
|||
В области низких частот ω ≤ |
0.1 |
сдвиг по фазе между выход- |
||
T |
|
|||
|
|
|||
|
1 |
|
|
|
ной и входной синусоидами практически отсутствует, а отношение амплитуды выходной синусоиды к амплитуде входной равно коэф-
фициенту усиления K. В области высоких частот ω ≥ 10 синусоиды
T2
43
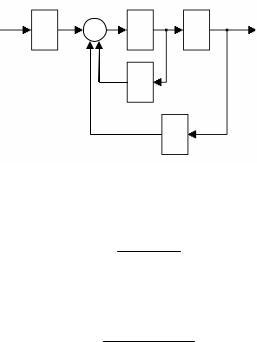
находятся почти в противофазе, а амплитуда на выходе во много раз меньше амплитуды входного сигнала.
Годограф передаточной функции W ( jω) на рис. 3.4, б также
показывает изменения амплитуды и фазы с ростом частоты от нуля до бесконечности.
Структурная модель системы с обратными связями по переменным состояния
Такой способ представления структурной математической модели известен как метод приведения к канонической форме.
Для системы второго порядка структурная схема показана на рис. 3.5, где координаты вектора состояния x1 и x2 выбраны в качестве выходных сигналов интеграторов.
u |
c |
+ |
– |
1 x2 |
1 x1 y |
|
s |
s |
|||
|
|
|
|
a
b
Рис. 3.5
Замыкая дважды контуры с обратными связями, находим выражение передаточной функции
W (s) = c . s2 + as +b
Разделив числитель и знаменатель этого выражения на коэффициент b, приведем передаточную функцию к виду колебательного устойчивого динамического звена
W (s) = K , T 2 s2 + 2ξTs +1
44
где коэффициент усиления K = bc , постоянная времени T = 1b , а
безразмерный коэффициент затухания ξ = ab . Корни характери-
стического уравнения колебательного устойчивого звена являются комплексно-сопряженными с отрицательной действительной частью, а это будет лишь в случае 0 <ξ <1.
Аналитическое выражение переходной характеристики колебательного устойчивого звена имеет вид
|
|
|
1 |
|
ξ |
|
1 − |
ξ |
2 |
|
1 - ξ |
2 |
|
|
|
|
|
|
|
−T t |
|
|
|
|
|
|
|
||||
h(t) = K |
1 |
− |
1 −ξ |
2 e |
sin |
T |
|
|
t + arctg ξ |
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где действительная часть корня − Tξ определяет затухание колеба-
ний, а мнимая часть |
1 −ξ2 |
частоту колебаний. |
|
T |
|||
|
|
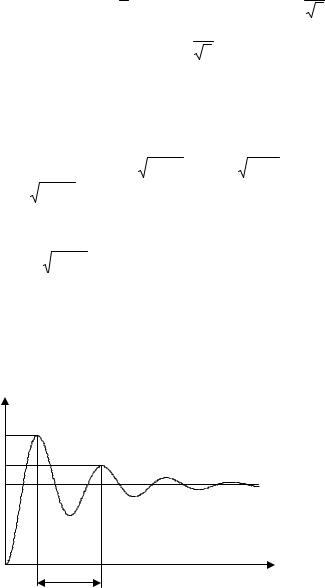
На рис. 3.6 представлен график этого переходного процесса, на котором показаны установившееся значение hуст, два первых максимальных значения hm1 и hm2, разделенные по времени на период колебания Tк.
Указанные значения будут использованы в работе для идентификации параметров модели колебательного звена.
h
hm1
hm2
hуст
Tк |
t |
Рис. 3.6
45
|
Амплитудная и фазовая частотные характеристики определяют- |
|||||||||||||||
ся выражениями |
|
|
|
|
|
K |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H (ω) = (1 −T 2ω2 )2 + 4ξ2T 2ω2 |
; |
|
||||||||
|
|
|
|
|
|
|
|
2ξTω |
|
; 0 ≤ω ≤ |
1 |
|
||||
|
|
|
|
|
θ |
|
−arctg |
1−T |
2 |
2 |
T , |
|
||||
|
|
|
|
|
(ω) = |
|
ω |
|
|
|
|
|||||
|
|
|
|
|
|
|
−π −arctg |
|
|
2ξTω |
2 ; ω > |
1 |
|
|||
|
|
|
|
|
|
|
1 |
−T |
2 |
T |
|
|||||
|
|
|
|
|
|
|
|
|
ω |
|
|
|||||
по |
|
|
которым |
строятся |
логарифмическая |
амплитудная |
||||||||||
L(ω) = 20lg H (ω) |
и фазовая частотные характеристики, приведен- |
|||||||||||||||
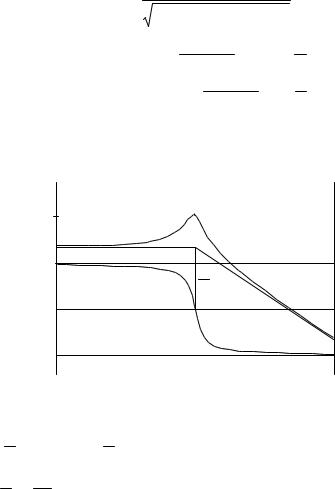
ные на рис. 3.7. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
L, дБ |
|
|
|
|
|
|
|
|
|
|
|
θ, град |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20lgK |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
|
|
|
|
|
-90 |
|
|
|
|
-40 |
|
|
|
|
|
|
|
|
|
|
|
-180 |
|
|
|
|
|
|
|
Рис. 3.7 |
|
|
|
|
|
||||
|
Из |
формул |
следует, что |
в точке |
сопряжения |
асимптот при |
||||||||||
ω = |
1 |
|
фаза |
1 |
|
а |
|
|
амплитудная |
характеристика |
||||||
T |
|
|
θ |
= −90°, |
|
|
||||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
= |
K |
. Подъем амплитудной характеристики будет тем боль- |
||||||||||||
H |
|
|
2ξ |
|||||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ше, чем меньше коэффициент затухания, причем максимум нахо- |
||||||||||||||||
46
дится не на этой частоте и не на собственной частоте ω =  1T−ξ2 , а
1T−ξ2 , а
в третьей точке ω =  1 − 2ξ2 .
1 − 2ξ2 .
T
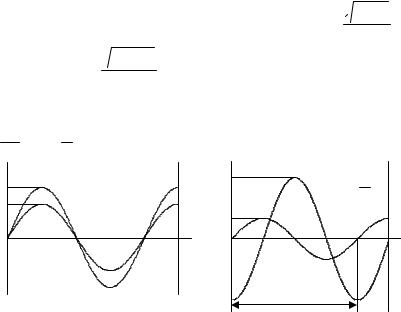
На рис. 3.8, а и б представлены осциллограммы, которые будем наблюдать при снятии частотных характеристик на частотах
ω ≤ |
0.1 |
и ω = |
1 |
соответственно. |
|
|
|
|
T |
|
T |
|
|
|
|
Aвых1 |
|
|
0.1 |
Aвых2 |
ω = |
1 |
|
|
|
ω < T |
|
T |
|||
Aвх |
|
|
|
Aвх |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
|
|
|
|
Tп |
|
|
|
|
|
а) |
Рис. 3.8 |
б) |
|
|
|
|
|
|
|
|
|
Отрезок времени для наблюдения Tп выбираем из области, где выходная синусоида практически установилась. С помощью такого эксперимента также можно идентифицировать параметры модели колебательного звена по значениям амплитуды входного Aвх и выходного Aвых сигналов.
Моделирование системы второго порядка с заданным расположением корней характеристического уравнения
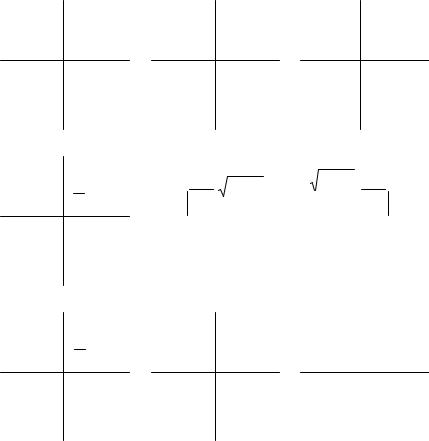
Структурная схема на рис. 3.5 позволяет реализовать не только колебательное звено, но и передаточные функции второго порядка с любым возможным расположением корней характеристического уравнения. Варианты расположения корней на комплексной плоскости s, представленные на рис. 3.9, можем получить, задавая различные значения по величине и знакам коэффициентов a и b структурной модели. Параметр c входит в состав коэффициента уси-
47
ления передаточной функции и на корни характеристического уравнения не влияет.
Im
××Re
а)
Im
×1
T
×Re
г)
Im
1
|
× |
T × |
||
− |
1 |
1 |
Re |
|
T |
|
T |
|
|
|
|
|
||
|
1 |
2 |
|
|
ж) |
|
|
|
|
Im |
Im |
− |
×1 × |
|
|
|
Re − |
×1 |
|
− |
×1 |
|
|
|
|
|
Re |
||||||||||
|
T |
|
|
|
|
T |
|
T |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|||
|
× |
|
Im |
|
|
|
|
|
|
1 −ξ2 |
|
Im |
× |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 −ξ2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ξ |
|
|
|
|
|
Re |
|
|
|
|
|
|
|
ξ |
|
Re |
||||||||
− T × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T × |
|
|
||||||
|
|
д) |
|
|
|
|
|
|
|
|
|
|
|
|
е) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
× |
× |
|
Re |
|
|
|
|
|
|
× |
|
× |
Re |
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
|
T2 |
|
|
|
|
з) |
|
|
|
|
|
|
|
|
|
|
и) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рис. 3.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Условия, при которых корни располагаются, как показано на рис. 3.9, а также соответствующие выражения передаточных функций приведены в таблице 1.
48
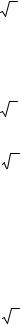
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.1 |
||||||
Рисунок |
Параметры модели |
Передаточная функция W(s) |
|||||||||||||||||
3.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
a =b = 0 |
|
|
|
K |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
б) |
a > 0, b = 0 |
|
|
|
K |
||||||||||||||
|
|
|
|
|
|
|
|
|
s(Ts +1) |
|
|
|
|
|
|
|
|||
в) |
a > 0, b > 0 |
|
|
|
K |
||||||||||||||
|
|
a > 2 b |
|
(T1s +1)(T2 s +1) |
|
||||||||||||||
г) |
a = 0, b > 0 |
|
|
|
K |
||||||||||||||
|
|
|
|
|
|
|
|
|
T 2 s2 +1 |
|
|
|
|
|
|||||
д) |
a > 0, b > 0 |
|
|
|
K |
||||||||||||||
|
|
a < 2 b |
|
T 2 s2 + 2ξTs +1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
е) |
a < 0, b > 0 |
|
|
|
K |
||||||||||||||
|
|
a |
|
|
< 2 b |
|
T 2 s2 − 2ξTs +1 |
|
|
|
|||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ж) |
a ≥ 0, b < 0 |
|
|
|
K |
||||||||||||||
|
|
|
|
|
|
a < 0 |
|
(T1s +1)(T2 s −1) |
|
||||||||||
з) |
a < 0, b = 0 |
|
|
|
K |
||||||||||||||
|
|
|
|
|
|
|
|
|
s(Ts −1) |
|
|
||||||||
и) |
a < 0, b > 0 |
|
|
|
K |
||||||||||||||
|
|
a |
|
|
> 2 b |
|
(T1s −1)(T2 s −1) |
|
|||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что для случая в) получаем третий способ моделирования передаточной функции из двух апериодических звеньев, реализованных вначале с помощью последовательного и параллельного соединения. С точки зрения помехозащищенности и стабильности схема на рис. 3.5 обладает преимуществами по сравнению с двумя предыдущими, поскольку за счет обратных связей в ней происходит
49
компенсация влияния возмущающих воздействий и изменений параметров элементов.
Информация о переходных и частотных характеристиках в двух случаях расположения корней в) и д) представлена в работе, а для остальных вариантов ее предстоит получить самостоятельно.
Анализ свободного движения в системе второго порядка
Для системы второго порядка n-мерное пространство переменных состояния сводится к так называемой фазовой плоскости, где по оси абсцисс откладывается первая координата вектора состояния x1, в качестве которой выбираем выходной сигнал, а по оси ординат вторая координата x2 в виде ее скорости изменения x2 = x1 .
Общее решение уравнений состояния задает на фазовой плоскости фазовую траекторию, параметром вдоль которой является время. Направление движения по фазовой траектории строго определено, поскольку если скорость x2 > 0, то выход x1 может только увеличиваться, и, наоборот, при x2 < 0 x1 уменьшается.
Анализируя устойчивость положения равновесия линейной системы в нуле, следует рассмотреть на фазовой плоскости лишь свободную составляющую движения, отбросив вынужденную составляющую. При моделировании это означает, что входное воздействие на структурную схему отсутствует u = 0, а движение в системе происходит из-за ненулевых начальных условий x10 и x20, заданных на интеграторах.
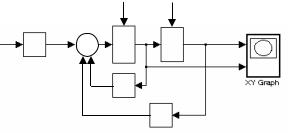
Для наблюдения с помощью осциллографа фазовых траекторий отключают его развертку, а на входы X и Y подают, соответственно, координаты вектора состояния x1 и x2, как показано на рис. 3.10.
|
|
|
x20 |
x10 |
|
c |
+ |
– |
1 x2 |
1 x1 |
|
s |
s |
||||
|
|
||||
|
|
|
a
b
Рис. 3.10
50
