12.2. Вычисление поверхностного интеграла II рода

Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.

Пусть функция R(x;y;z) непрерывна на всех точках поверхности S, заданной уравнением z = z(x;y), где z(x;y) – непрерывная функция в замкнутой области D (или D_xy)- проекция поверхности S на плоскость Oxy.

Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда (i = 1, 2, …, n).

Так как , то интегральная сумма (12.1) может быть записана в виде

(12.2)

Правая часть этого равенства есть интегральная сумма для функции ,непрерывной в области D. Переходя к пределу в равенстве (12.2) при , получаем формулу

(12.3)

выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т.е. нижнюю, поверхности S, то полученный двойной интеграл берут со знаком «минус». Поэтому

(12.4)

Аналогично

(12.5)

(12.6)

где D_xz и D_yx – проекции поверхности S на плоскость Oxz и Oyz соответственно (замкнутые области).

В формуле (12.5) поверхность S задана уравнением y = y(x;z), а в формуле (12.6) – уравнением x = x(y;z). Знаки интеграла выбираются в зависимости от ориентации поверхности S (так, в формуле (12.5) берем знак «плюс», если нормаль к поверхности образует с осью Оу острый угол, а знак «минус» - если тупой угол).

Для вычисления общего поверхностного интеграла II рода используют формулы (12.4) – (12.6), проектируя поверхность S на все три координатные плоскости:

Замечание. Можно показать справедливость равенств

(12.7)

где ds – элемент площади поверхности S; cosα, cosβ, - направляющие косинусы нормали к выбранной стороне поверхностиS.

Поверхностные интегралы I и II рода связаны соотношением

(12.8)

Пример 12.1. Вычислить

по верхней стороне части плоскости б лежащей вIV октанте

Решение: На рисунке 21 изображена заданная часть плоскости. Нормаль , соответствующая указанной стороне поверхности, образует с осьюОу тупой угол, а с осями Ох и Oz – острые. В этом можно убедится, найдя косинусы нормального вектора плоскости:

Поэтому перед двойными интегралами в формулах (12.4) и (12.6) следует брать Рис. 21.

знак «плюс», а в формуле (12.5) – знак «минус». Следовательно,

12.3. Формула Остроградского – Гаусса

Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченной этой поверхностью устанавливает следующая теорема.

Теорема 12.1. Если функция P(x;y;z), Q(x;y;z), R(x;y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула

(12.9)

где S – граница области V и интегрирование по S производится по ее внешней стороне.

Формула (12.9) называется формулой Остроградского – Гаусса (является аналогом формулы Остроградского - Грина).

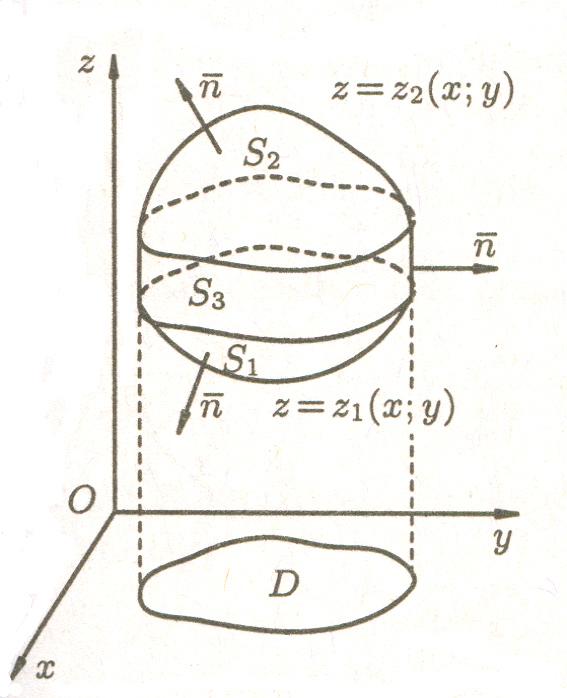
Пусть область V ограничена снизу поверхностью S₁, уравнение которой z = z₁(x;y); сверху - поверхностью S₂, уравнение которой z = z₂(x;y) (функции z₁(x;y) и z₂(x;y) непрерывны в замкнутой плоскости D – проекции V на плоскость Oxy, ); сбоку – цилиндрической поверхностью S₃, образующие которой параллельны оси Oz (см. рис. 22).

Рассмотрим тройной интеграл

Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей S₁ и S₂ соответственно (см. (12.3)). Получаем:

Добавляя равный нулю интеграл по внешней сторонеS₃, получим:

или

(12.10)

Рис. 22. где S поверхность, ограничивающая область V.

Аналогично доказываются формулы

(12.11)

(12.11)

Складывая почленно равенства (12.10), (12.11) и (12.12), получаем формулу (12.9) Остроградского – Гаусса.

Замечания.

1. Формула (12.9) считается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.

2. Формулу Остроградского – Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.

Пример 12.2. Вычислить гдеS – внешняя сторона пирамиды, ограниченной плоскостями

Решение: По формуле (12.9) находим:

Заметим, что интеграл I₁ (см. пример. 12.1) можно вычислить иначе:

где поверхности S₂, S₃, S₄ есть соответственно треугольники OAC, AOB, COB (см. рис. 23).

Имеем:

Рис. 23.