Глава III. Криволинейные и поверхностные интегралы

Обобщением определенного интеграла на случай, когда область инте­грирования есть некоторая кривая, является так называемый криволи­нейный интеграл.

§9. Криволинейный интеграл I рода

9.1. Основные понятия

Пусть на плоскости Oxy задана непрерывная кривая АВ (или L) дли­ны I. Рассмотрим непрерывную функцию f(x;у), определенную в точках дуги АВ. Разобьем кривую АВ точками Мо = А, М₁ ,М₂,…, М_п = В на п произвольных дуг М_i-1 М_i с длинами Δl_i (i = 1, 2, ... , n) (см. рис. 1). Выберем на каждой дуге М_i-1 М_i произвольную точку и составимсумму

(9.1)

Рис. 1.

Ее называют интегральной суммой для функции f(x;у) по кривой АВ.

Пусть λ = Δl_i — наибольшая из длин дуг деления. Если при λ→0 (тогда n→∞) существует конечный предел интегральных сумм (1), то его называют криволинейным интегралом от функции f(х; у) по длине кривой АВ (или I рода) и обозначают (или).

Таким образом, по определению,

(9.2)

Условие существования Криволинейного интеграла I рода (существования интегральной суммы (9.1)) при n→∞ (λ→0)) представляет следующая теорема, которую мы приводим здесь без доказательства.

Теорема 9.1. Если функция f(x;y) непрерывна в каждой точке гладкой кривой (в каждой точке (x;y) Є L существует касательная к данной кривой и положение ее непрерывно меняется при перемещении точки по кривой), то криволинейный интеграл I рода существует, и его величина не зависит ни от способа разбиения кривой на части, ни от выбора точек в них.

Аналогичным образом вводиться понятие криволинейного интеграла от функции f(x;y;z) по пространственной кривой L.

Приведем основные свойства криволинейного интеграла по длине дуги (I рода).

1. , т.е. криволинейный интегралI рода не зависит от направления интегрирования.

2. ,с=const.

3. .

4. , если путь интегрирования L разбит на части L₁ и L₂ такие, что L = L₁ L₂ и L₁ и L₂ имеют единственную общую точку.

5. Если для точек кривой L выполнено неравенство f₁(x;y) ≤ f₂(x;y), то .

6. , где l – длина кривой AB.

7. Если функция f(x;y) непрерывна на кривой AB, то на этой кривой найдется точка (x_c;y_c) такая, что (теорема о среднем).

9.2. Вычисление криволинейного интеграла I рода

Вычисление криволинейного интеграла I рода может быть сведено к вычислению определенного интеграла. Приведем без доказательства правила вычисления криволинейного интеграла I первого рода в случаях, если кривая L задана параметрическим, полярным и явным образом.

Параметрическое представление кривой интегрирования

Если кривая AB задана параметрическими уравнениями x = x(t), y = y(t), t Є [α;β], где x(t) и y(t) – непрерывно дифференцируемые функции параметра t, причем точке A, соответствует t = α, а точке B – значение t = β, то

(9.3)

Аналогичная формула имеет место для криволинейного интеграла от функции f(x;y;z) по пространственной кривой AB, задаваемой уравнениями x = x(t), y = y(t), z = (t), :

(9.4)

Явное представление кривой интегрирования

Если кривая AB задана уравнением y = φ(x), x Є [a;b], где φ(x) – непрерывно дифференцируемая функция, то

(9.5)

Подынтегральное выражение в правой части формулы (9.5) получается заменой в левой части y = φ(x) и (дифференциал дуги кривой).

Пример 1. Вычислить , гдеL – отрезок прямой между точками O(0;0) и A(4;3).

Решение: Уравнение прямой OA есть y = . Согласно формуле (9.5), имеем:

.

Полярное представление кривой интегрирования

Если плоская кривая L задана уравнением r = r(), в полярных координатах, тои(9.6)

Подчеркнем, что нижний предел определенного интеграла в формулах (9.3) – (9.6) должен быть меньше верхнего.

Пример 2. Вычислить , гдеL – лепесток лемнискаты , расположенной вI координатном углу.

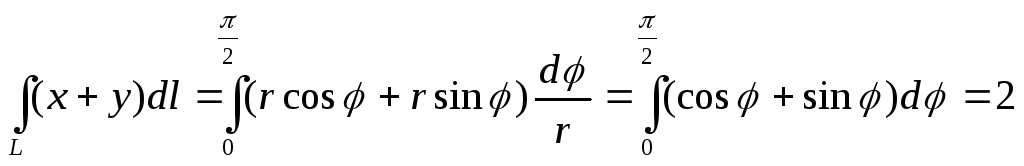
Решение: Кривая интегрирования изображена на рисунке 2. Воспользуемся формулой (6). Так как , то, заметив, что , получаем:Рис. 2.