Кулик Введение в теорию квантовых вычислений Книга 2 2008

1.8.Собственные значения и собственные векторы

Вобщем случае, кэт-вектор X|A не равен константе, умноженной на |A . Однако имеются специальные кэт-векторы, которые называются собственными векторами оператора X. Они обозначаются

и обладают свойством

где χ′, χ′′ — числа, называемые собственными значениями. Таким образом, действие оператора Х на один из его собственных векторов дает тот же самый собственный вектор, умноженный на соответствующее собственное значение.

Рассмотрим собственные векторы и собственные значения эрмитового оператора ξ. Для них выполнено уравнение

где |ξ′ — собственный вектор, связанный с собственным значением ξ′. Легко выводятся три важных результата.

1) Все собственные значения являются действительными числами, а собственные векторы, отвечающие разным собствен-

ным значениям, ортогональны. Так как оператор ξ эрмитовый, то уравнение, дуальное к (1.44) (для собственного значения ξ′′) имеет следующий вид:

Если умножить (1.44) слева на 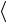ξ′′ , а (1.45) — справа на | ξ′ и

Предположим, что собственные значения ξ′ и ξ′′ равны друг другу. Тогда из (1.46) следует, что

где мы использовали тот факт, что | ξ′ является ненулевым кэт-

вектором. Отсюда можно сделать вывод, что собственные значения являются действительными числами. Пусть теперь собственные значения ξ′ и ξ′′не равны друг другу. Отсюда следует, что

т. е. собственные векторы, отвечающие различным собственным значениям, ортогональны.

2) Собственные значения, связанные с собственными кэтвекторами, совпадают с собственными значениями, связанными с собственными бра-веторами. Собственный бра-вектор оператора ξ, соответствующий собственному значению ξ′, определяется уравнением

3) Дуальным к собственному кэт-вектору является собственный бра-вектор, принадлежащий тому же собственному значению, и обратно.

1.9. Наблюдаемые

Мы развили математический формализм, содержащий объекты трех типов: бра-векторы, кэт-векторы и линейные операторы. Как было показано, кэт-векторы можно использовать для представления возможных состояний микроскопической системы. Однако существует одно-однозначное соответствие между элементами кэтпространства и дуальными им элементами бра-пространства. Поэтому мы вправе заключить, что бра-векторы также можно использовать для представления состояний микроскопической системы. А что можно сказать о динамических переменных, описывающих систему (например, ее координате, импульсе, энергии, спине и пр.)? Каким образом они могут быть включены в развиваемый нами формализм? Мы видим, что единственные оставшиеся неиспользованными объекты — это операторы. Таким образом, мы

32

высказываем предположение, что динамические переменные мик-

роскопической системы представляются линейными операторами, действующими на бра- и кэт-векторы, которые соответствуют различным возможным состояниям системы. Заметим, что операторы должны быть линейными, в противном случае, действуя на бра/кэт, которые направлены в одну сторону, но имеют разную длину, эти операторы могут в общем случае выдавать на выходе бра/кэт, направленные в разные стороны. Так как длины бра- и кэтвекторов не имеют физического смысла, разумно предположить, что это же относится к нелинейным операторам.

Мы видели, что если наблюдать состояние поляризации фотона, поместив на пути фотона поляроид, то в результате фотон перейдет в состояние с поляризацией, параллельной или перпендикулярной оптической оси поляроида. Первое состояние поглощается, а второе проходит сквозь поляроид. В общем случае, мы не можем предсказать, в какое состояние перейдет данный фотон, такое предсказание может быть только статистическим. Однако мы знаем, что если фотон начально поляризован параллельно оптической оси, то он безусловно будет поглощен поляроидом, а если фотон начально поляризован перпендикулярно оптической оси, то он безусловно пройдет сквозь поляроид. Мы знаем также, что после прохождения пленки фотон должен находиться в состоянии поляризации, перпендикулярной оптической оси (в противном случае он не мог бы пройти сквозь поляроид). Можно вторично провести наблюдение состояния поляризации такого фотона, поместив сразу за первым поляроидом точно такой же второй поляроид (с той же ориентацией оптической оси). Ясно, что фотон безусловно пройдет сквозь второй поляроид.

Состояния поляризации фотона не являются чем-то особенным. Таким образом, в более общем виде можно сказать, что когда производится измерение динамической переменной микроскопической системы, сама система совершает переход в одно из ряда независимых состояний (заметим, что перпендикулярные и параллельные состояния поляризации фотона линейно независимы). В общем случае, каждое из этих конечных состояний связано с разным результатом измерения, т. е. с разным значение динамической переменной. Заметим также, что результатом измерения должно быть действительное число (не существует измерительных приборов,

33

дающих на выходе комплексные числа). Наконец, если наблюдение сделано и получено, что система находится в некотором определенном конечном состоянии с определенным значение динамической переменной, то второе наблюдение, сделанное немедленно после первого, с достоверностью обнаружит систему в том же состоянии с тем же значением динамической переменной.

Как отразить все эти факты в развиваемом математическом формализме? Призвав на помощь интуицию, мы предполагаем, что

измерение динамической переменной, соответствующей оператору X в кэт-пространстве, заставляет систему перейти в состояние, соответствующее одному из собственных кэт-векторов опе-

ратора Х. Неудивительно, что такое состояние называется собст-

венным состоянием. Кроме того, результат измерения есть собственное значение, связанное с собственным вектором, в который перешла система. Тот факт, что результат измерения должен быть действительным числом, приводит к условию, что динамические переменные могут описываться только эрмитовыми оператора-

ми (так как только такие операторы гарантированно имеют действительные собственные значения). Утверждение, что собственные векторы эрмитового оператора, соответствующие разным собственным значениям (т. е. разным результатам измерения), ортогональны, находится в соответствии с нашим высказанным ранее требованием, что состояния, в которые перескакивает система, должны быть взаимно независимыми. Можно сделать вывод, что результат измерения динамической переменной, представленной эрмитовым оператором ξ, должен быть одним из собственных значений этого оператора. Обратно, каждое собственное значение ξ является возможным результатом измерения, осуществленного над соответствующей динамической переменной. Это позволяет придать собственным значениям физический смысл. (С этого момента для простоты мы не будем делать различия между состоянием и представляющим его кэт-вектором, а также между динамической переменной и представляющим ее оператором.)

Разумно предположить, что если измеряется некоторая динамическая переменная ξ и при этом система находится в определенном состоянии, то состояния, в которые может перейти система в результате измерения, таковы, что исходное состоя-

ние зависит от них. Это довольно безобидное утверждение имеет

34

два очень важных следствия. Во-первых, сразу же после наблюдения, результатом которого является определенное собственное значение ξ′, система остается в соответствующем собственном состоянии. Однако это собственное состояние ортогонально (т. е. независимо) любому другому собственному состоянию, отвечающему другому собственному значению. Отсюда следует, что второе измерение, совершенное немедленно после первого, должно оставить систему в собственном состоянии, соответствующем собственному значению ξ′. Иными словами, второе измерение вынуждено дать тот же результат, что и первое. Более того, если система находится в собственном состоянии ξ, соответствующем собственному значению ξ′, то измерение ξ обязательно приводит к ре-

зультату ξ′. Это следует из того, что система не может перейти в собственное состояние, соответствующее другому собственному значению ξ, так как подобное состояние не зависит от исходного. Во-вторых, можно утверждать, что измерение ξ должно всегда давать какой-то результат. Отсюда вытекает, что вне зависимости от начального состояния системы всегда возможно перейти в одно из собственных состояний ξ. Другими словами, произвольный кэтвектор всегда должен зависеть от собственных векторов оператора ξ. Такое возможно только в том случае, если собственные векторы образуют полный набор состояний (т. е. на них натянуто пространство кэт-векторов). Следовательно, чтобы эрмитовый оператор ξ соответствовал наблюдаемой величиной, его собственные векторы должны образовывать полный набор. Часто сам эрмитовый оператор, удовлетворяющий этому условию, называется наблюдаемой. Таким образом, любая наблюдаемая величина должна быть эрмитовым оператором с полным набором собственных состояний.

1.10. Измерения

Мы видели, что измерение некоторой наблюдаемой ξ микроскопической системы вынуждает систему перейти в одно из собственных состояний ξ. Результатом измерения является соответствующее собственное значение (или некоторая функция этого значения). Невозможно определить, в какое собственное состояние пе-

35

рейдет данная система, но можно предсказать вероятность такого перехода. Чему же равна вероятность того, что система, находя-

щаяся в некотором начальном состоянии A , совершит переход в собственное состояние ξ′ наблюдаемой ξ в результате осуществленного над системой измерения? Начнем с простейшего случая. Если система начально находится в состоянии ξ′ , то вероятность перехода в состояние ξ′′ , соответствующее другому собственному значению, равна нулю, а вероятность перехода в то же самое собственное значение ξ′ равна единице. Удобно нормировать

собственные векторы таким образом, чтобы они все имели единичную норму. Из свойства ортогональности собственных векторов следует, что

где δξ′ξ′′ равен единице, если ξ′= ξ′′, и нулю в остальных случаях.

Мы сейчас предполагаем, что все собственные значения ξ различны.

Заметим, что вероятность перехода из начального собственного состояния ξ′ в конечное собственное состояние ξ′′ совпадает

со значением внутреннего произведения 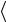ξ′ ξ′′ . Можно ли ис-

пользовать это соответствие, чтобы получить общее правило для вычисления вероятностей переходов? Предположим, что система

начально находится в состоянии A , которое не является собственным состоянием ξ. Можно ли отождествить вероятность перехода в конечное состояние ξ′ с внутренним произведением

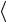A ξ′ ? Ответ отрицателен, так как 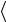A ξ′ в общем случае являет-

ся комплексным числом, а комплексные вероятности имеют мало смысла. Попробуем еще раз. А как насчет того, что мы отождествим вероятность перехода с квадратом модуля внутреннего произ-

ведения |A ξ′ |2? Эта величина есть безусловно положительное число (и может поэтому интерпретироваться как вероятность). Это

36

предположение дает также правильный ответ для вероятностей переходов между собственными состояниями. Мы, на самом деле, угадали верно.

Так как собственные состояния наблюдаемой ξ образуют полный набор, можно выразить любое данное состояние A как их линейную комбинацию. Легко показать, что

где суммирование производится по всем различным собственным значениям ξ, и использованы формула (1.20) и тот факт, что собственные состояния взаимно ортогональны. Заметим, что все полученные выше результаты вытекают из чрезвычайно полезного (и легко доказываемого) результата:

где 1 означает тождественный оператор. Относительная вероят-

1.11. Средние значения

Рассмотрим ансамбль микроскопических систем, приготовленных в одном и том же начальном состоянии A . Пусть над каждой

системой производится измерение наблюдаемой ξ. Мы знаем, что каждое измерение дает значение ξ′ с вероятностью P(ξ′). Чему равно среднее значение измеренной величины? Эта величина, которая в общем случае называется иначе математическим ожиданием ξ, задается выражением

что сводится к

с помощью (1.54).

Рассмотрим тождественный оператор 1. Все состояния являются собственными состояниями этого оператора с собственным значением единица. Таким образом, среднее значение этого оператора всегда равно единице, т. е.

для всех A .

1.12. Вырождение

Предположим, что два разных собственных состояния ξ′a и

ξ′b оператора ξ соответствуют одному собственному значению ξ′.

Такие собственные состояния называют вырожденными. Эти состояния с необходимостью ортогональны любым собственным состояниям, соответствующим разным собственным значениям, но в общем случае они не ортогональны друг другу (т. е. доказатель-

38

ство ортогональности в разд. 1.8 в этом случае не работает). Это печально, так как значительная часть описанного формализма критически зависит от взаимной ортогональности разных собственных состояний наблюдаемой. Заметим, однако, что любая линейная

комбинация ξ′a и ξ′b также является собственным состояниям,

соответствующим собственному значению ξ′. отсюда вытекает, что всегда можно построить два взаимно ортогональных вырожденных собственных состояния. Например,

Этот результат легко обобщается на случай более чем двух вырожденных собственных состояний. Можно сделать вывод, что для любой данной наблюдаемой всегда возможно построить полный набор взаимно ортогональных собственных состояний.

1.13. Совместные наблюдаемые

Предположим, что мы хотим одновременно измерить две наблюдаемые ξ и η микроскопической системы. Допустим, что у нас есть два прибора, способных измерять две наблюдаемые ξ и η, соответственно. Например, двумя наблюдаемыми могут быть проекции спинового углового момента частицы со спином 1/2 на оси x и z, соответственно. Они могут быть измерены с помощью установки опыта Штерна–Герлаха. Предположим, что мы совершили измерение ξ, и система была переброшена в одно из собственных

состояний ξ — ξ′ с собственным значением ξ′. Что произойдет, если мы теперь осуществим измерение η? Предположим, что собственное состояние ξ′ является также собственным состоянием η

с собственным значением η′. В этом случае измерение η с определенностью даст результат η′. Вторичное измерение ξ с определенностью даст результат ξ′, и т. д. В этом смысле мы можем сказать, что наблюдаемые ξ и η одновременно имеют собственные значения ξ′ и η′, соответственно. Ясно, что если все собственные состояния ξ

39

являются также собственными состояниями η, то всегда возможно совершить одновременное измерение наблюдаемых ξ и η. Такие наблюдаемые называются совместными (или одновременно измеримыми).

Предположим, однако, что собственные состояния ξ не являются собственными состояниями η. Возможно ли при этом измерить обе наблюдаемые одновременно? Совершим опять наблюдение x,

переводящее систему в собственное состояние ξ′ с собственным

значением ξ′. Теперь можно совершить второе наблюдение для определения η. Это переведет систему в одно (из многих) собст-

венных состояний η, зависящих от ξ′ . В принципе, каждое из

этих собственных состояний связано с различными результатами измерения. Предположим, что система перешла в собственное со-

стояние η′ с собственным значением η′. Другое измерение ξ перебросит систему в одно (из многих) собственных состояний η, которое зависит от η′ . Каждое собственное состояние снова свя-

зано с различными возможными результатами наблюдений. Ясно, что если наблюдаемые ξ и η не имеют совместных собственных состояний, то, если значение ξ известно (т. е. система находится в собственном состоянии ξ), значение η не определено (т. е. система не находится в каком-то собственном состоянии η), и наоборот. Мы говорим, что две наблюдаемых несовместны.

Как мы видели, условие одновременной измеримости двух наблюдаемых ξ и η состоит в том, что они должны иметь совместные собственные состояния (т. е. каждое собственное состоя-

ние оператора ξ должно быть собственным состоянием оператора η). Предположим, что так оно и есть. Пусть произвольное собственное состояние ξ с собственным значением ξ′ является также собственным состоянием η с собственным значением η′. Удобно

обозначить это совместное собственное состояние ξ′η′ . Имеем: