Кулик Введение в теорию квантовых вычислений Книга 2 2008

Здесь для коэффициентов T и R использованы значения (2.182) и (2.183), а последнее слагаемое в фигурной скобке, обозначенное как (1 2 ), получается из первого слагаемого перестановкой

индексов.

Выходное состояние out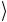 (2.186) содержит слагаемые, кото-

рые отвечают следующим трем возможным результатам воздействия светоделителя:

(1)оба фотона имеют волновой вектор k,

(2)оба фотона имеют волновой вектор −k,

(3)фотоны имеют противоположные волновые

векторы, k и –k.

Как видно из рис. 2.11, в первом случает оба фотона оказываются справа от светоделителя, а во втором случае — слева. Таким образом для этих двух исходов оба фотона находятся по одну сторону от светоделителя. В третьем случае фотоны оказываются по одному с каждой стороны от светоделителя.

Произведем такое совместное измерение над системой двух фотонов, когда два детектора, расположенные в выходных каналах светоделителя по одному с каждой стороны, регистрируют совпадение фотоотсчетов1. Амплитуда вероятности такого события определяется, очевидно, только теми слагаемыми в выражении (2.186), в которые входят однофотонные состояния с противоположными волновыми векторами. Эти члены имеют вид

где Ψ(−) 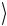определяется формулой (2.175).

1 Детекторы регистрируют акты попадания на них фотонов безотносительно к их поляризациям.

151

При преобразовании выражения, стоящего в фигурной скобке в (2.187), было учтено, что одночастичные состояния ±kλ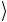 можно

записать формально как произведение λ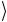 ±k векторов состоя-

ний, относящихся к пространственным (внешним) и поляризационным (внутренним) степеням свободы. В результате вектор двухчастичного состояния (2.187) факторизовался. Обратим внимание на важные особенности состояния (2.187). Прежде всего, оно, конечно, симметрично относительно перестановки фотонов 1 и 2. Далее, знак минус при втором слагаемом в фигурной скобке возник, как это видно из предыдущего выражения (2.186), из-за вели-

чины R2 = (−i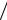 2 )2 = −12 . В факторизованном выражении

(2.187) пространственные и поляризационные состояния являются антисимметричными относительно перестановки частиц. Подчеркнем, что при заданном нами начальном условии результат (2.187) формируется единственным образом, когда на выходе два фотона находятся по разные стороны от светоделителя. Результатом регистрации совпадения фотоотсчетов двух детекторов является проектирование поляризационного состояния двухфотонной системы

на антисимметричное состояние Белла Ψ(−) .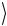

Светоделитель является линейной оптической системой. Выше было продемонстрировано, как с его помощью можно выделить

состояние Ψ(−) 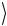. Светоделитель можно использовать для иденти-

фикации состояния Ψ(+) 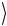. При этом надо регистрировать пару

фотонов по одну сторону от светоделителя. Далее потребуются еще поляризационные измерения, чтобы отличить симметричное

состояние Ψ(+) 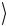от других симметричных состояний Φ(±) 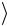. Ана-

лиз же последних нуждается в более сложных нелинейнооптических процессах.

В настоящее время экспериментально реализовано измерение полного набора поляризационных состояний Белла.

152

Состояния Гринбергера-Хорна-Цайлингера

Рассмотренные выше двухчастичные спиновые или поляризационные системы позволяют понять квантовую суть явления перепутывания. В процессах хранения и манипулирования квантовой информацией в многокубитовых регистрах определяющую роль играет перепутывание состояний большого числа частиц. Перепутанные состояния более чем двух частиц называют состояниями Гринбергера-Хорна-Цайлингера (ГХЦ). По сравнению с двухкубитовой ситуацией ГХЦ-перепутывание обладает гораздо более широким спектром специфических корреляционных свойств, находящихся в резком противоречии с классическими представлениями. Это важно не только с точки зрения принципиальных оснований квантовой механики, но и применительно к задачам квантовой информации. Мы не будем вдаваться в обсуждение этих вопросов, но для полноты картины приведем один пример трехчастичного максимально перепутанного состояния ГХЦ.

Рассмотрим систему, состоящую из трех частиц со спином 12 . Суммарный спин может быть равен S = 32 . Это максимальное значение. При таком S максимальное значение проекции на ось z равно 32 и получается, когда каждый спин имеет проекцию 12 . Минимальное значение проекции, равное −32 , получается, когда каждый спин имеет проекцию −12 . Состояние

является, очевидно, максимально перепутанным. Оно симметрично относительно перестановки частиц. Ни один из трех кубитов не несет сам по себе определенной информации о своем спиновом состоянии. Любое из двух возможных значений проекции его спина является равновероятным. Но как только будет произведено измерение проекции спина на ось z одного из кубитов и получено

153

какое-то значение, состояния двух других кубитов станут строго определенными. И этот результат не зависит от пространственного расположения частиц, над которыми производятся измерения.

Задачи

1. Доказать, что кэт-векторы

являются собственными состояниями квадрата оператора суммар-

щими собственным значениям S (S +1) соответственно для S =1 и S = 0 .

Указание

В спинорном представлении рассматриваемые состояния имеют вид

где верхние индексы показывают номер частицы.

2. Доказать, что перепутанное состояние

описывается таким же по форме выражением в базисе собственных векторов оператора проекции спина на любую ось n .

154

Указание

Написать собственные векторы оператора

проекции спина 12 на ось n ={nx , ny , nz } , n2 =1, и разложить однокубитовые состояния ±12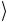1,2 по этому базису.

3. Написать матрицу плотности произвольного чистого спинового состояния (2.30).

Решение

Произвольное (чистое) спиновое состояние описывается кэтвектором

где матрица плотности ρσσ ' в Sz – представлении имеет вид

Из этого выражения видно, что

Spρˆ = ∑ρσσ = ∑Cσ 2 =1.

σσ

155

Для матрицы ρˆ 2 имеем

ρˆ 2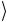 = ψψ ψψ = ψ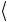ψ = ρˆ .

В этом можно убедиться и непосредственным перемножением матриц:

4. Доказать, что для энтропии фон Неймана квантового состояния с матрицей плотности ρˆ имеет место следующее соотношение:

S(ρˆ) = −Sp(ρˆ log2 ρˆ) = −∑pj log2 pj ,

j

где pj – собственные значения эрмитового неотрицательного оператора ρˆ .

Доказательство

Пусть { j} – полный ортонормированный базис, который диаго-

нализует матрицу плотности, т.е. имеет место следующее спектральное разложение оператора ρˆ

ρˆ = ∑pj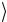 j j ,

j

где числа pj ≥ 0 ( ∑pj =1) есть собственные значения оператора

j

ρˆ . По определению спектрального разложения функции от оператора имеем

log2 ρˆ = ∑(log2 pj ) j j .

j

156

Тогда

= ∑pj log2 pj .

j

Тем самым, интересующее нас соотношение доказано. При вычислении мы воспользовались условием ортонормированности базиса,

j i = δji , линейностью операции взятия следа и тем, что

Sp j j = j j =1.

5. Матрицу плотности произвольного (чистого) спинового состояния привести к диагональному виду и вычислить для этого состояния энтропию фон Неймана.

Решение

Поскольку произвольное (чистое) спиновое состояние ψ являет-

ся собственным состоянием оператора проекции спина sˆn на некоторую ось n (см. задачу 3 в конце раздела 2.2), отвечающее, например, собственному значению sn =12 , то в базисе состоя-

ний sn = ±1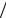2 кэт-вектор имеет вид

ψ = ∑Cσ σ = sn =12 .

σ

Тогда для ρˆ получаем

ρˆ = ψψ = sn =12sn =12 ,

157

т.е. в этом базисе матрица плотности

имеет единственный отличный от нуля матричный элемент, который стоит на диагонали и равен 1. Другими словами, спектральное

разложение ρˆ содержит только одно слагаемое, отвечающее собственному значению p =1. Тогда log2 ρˆ = 0 , и энтропия фон Неймана чистого состояния S(ρˆ) = 0 .

6. Написать матрицу плотности спинового состояния одной из частиц ЭПР-пары, находящейся в состоянии Белла.

Решение

Рассмотрим перепутанное состояние Ψ(−) 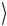. Матрица плотности одной из частиц, например первой, получается из выражения для оператора плотности системы Ψ(−)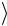 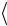Ψ(−) с помощью операции взятия следа по квантовым числам второй частицы, т.е.

Следовательно, матрица плотности ρˆ1 имеет диагональный вид

Собственные значения p±1 2 =12 , стоящие на диагонали, оказываются одинаковыми в полном соответствии с тем, что в максимально перепутанном состоянии Ψ(−) проекция спина одной из

частиц ЭПР-пары является полностью неопределенной и с равными вероятностями принимает любое из своих возможных значений

±12 . Тогда энтропия фон Неймана состояния с матрицей плотности ρˆ1 имеет вид

S(ρˆ1) = −Spρˆ1 log2 ρˆ1 = −(p12 log2 p12 + p−12 log2 p−12 )= = −log2 12 =1.

Это есть максимально возможное значение энтропии фон Неймана для состояния, которое описывается матрицей плотности 2×2 (см. следующую задачу).

2

7. Доказать, что S(ρˆ) = −∑pj log2 pj , где pj ≥ 0 и p1 + p2 =1,

j=1

имеет максимальное значение 1 при условии, что p1 = p2 =1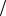2 .

Указание

Представить S в виде S( p) = −p log2 p −(1− p)log2 (1− p) и найти максимум функции S( p) .

8.Написать матрицу плотности спинового состояния одной из частиц ЭПР-пары, находящейся в перепутанных состояниях Φ(±) ,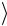

Ψ(+) . Вычислить энтропию фон Неймана.

9.Показать, что произвольная спиновая матрица плотности ρˆ мо-

жет быть представлена в виде

ρˆ = 12 (1+ aσ ),

159

где σi – матрицы Паули, вектор a является действительным, а его длина a ≤1.

Указание

Воспользоваться результатом задачи 4 в конце раздела 2.2, а также свойствами матриц Паули (2.41). В случае чистого состояния, ко-

10. Рассмотреть задачу об отражении и прохождении частицы с

U (z)=αδ(z), α > 0 . Убедиться, что при m2αk ≡ϑ =1 амплитуды

прохождения и отражения совпадают с формулами (2.182) и (2.183) с точностью до общего фазового множителя.

Решение

Так как U (z)=αδ(z), то стационарное уравнение Шрёдингера

d 2Ψ + 2m (E −U (z))Ψ = 0 dz2 2

при z ≠ 0 имеет вид

d 2Ψ2 + k 2 z = 0 .

dz

Ищем решение, описывающее частицу, падающую на потенциальный барьер слева.

160