
Корсун Гидродинамика ЯЕУ Сборник задач и упражнений 2008
.pdf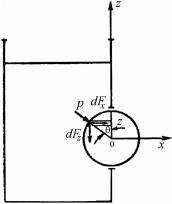
положной стороне поверхности Σ этот цилиндр вырежет некоторую площадку dσ′ с нормалью n′. Проекции на ось 0z сил, действующих на площадки dσ и dσ′, будут равны
dFSz = −p(z1 ) nz dσ, |
′ |
′ |
′ |
(1.9.3) |
|
dFSz = −p(z2 ) nz dσ |
, |
||||
где z1 и z2 – координаты площадок. |
n′z dσ′ = dσz , где |
|
|
||
Имея в виду, что nZ dσ = −dσz , а |
dσz |
– пло- |
|||
щадь поперечного сечения проведенного цилиндра, и что давление
в жидкости изменяется по закону p(z) = p(z = 0) + ρжg |
z , для сум- |
мы сил, действующих на площадки, найдем |
|
′ |
(1.9.4) |
dFSz + dFSz = −ρ g(z2 − z1)dσZ ≡ −ρжg dV , |
|
где dV ≡ (z2 − z1 )dσz – объем элементарного цилиндра. |
|
Интегрирование (1.9.4) дает |
|
FSz = −ρжgV . |
(1.9.5) |
С учетом (1.9.1) и (1.9.5) полная сила, действующая на тело, |
|
Fz = g(ρт − ρж )V . |
(1.9.6) |
Таким образом, на тело произвольной формы, погруженное в жидкость, кроме силы тяжести, действует выталкивающая сила, равная весу вытесненной телом жидкости. Это положение было установлено Архимедом.
1.10. В выбранной системе координат (рис. О3) давление в жидкости изменяется по закону
|
|
p(z) = p0 + gρж (h − z) . |
|
||||
Сила давления жидкости, дейст- |
|
||||||
вующая на полоску шириной r0dθ на |
|
||||||
высоте |
z = r0 cos θ от |
центра шара, |
|
||||
имеет две компоненты |
|
|
|
|
|||
|
|
dFx = p(r0 cosθ) dSx , |
, (1.10.1) |
|
|||
|
|
dF |
= −p(r cosθ) dS |
z |
|
||
|
|
z |
0 |
|
|
|
|
где dSx |
и |
dSz проекции площади по- |
|
||||
лоски |
dS = πr0 sin θr0dθ |
на направле- |
Рис. О3 |
||||
ния x |
и z: |
|
|
|
|
|
|
|
|
|
|
|
|
71 |
|

dSx = 2r02 sin2 θdθ,
dS |
z |
= π r2 sin θ cos θ dθ. |
(1.10.2) |
|
0 |
|
Результирующие значения сил находятся интегрированием по поверхности полусферы. Постоянная составляющая в p(z) , равная
внешнему давлению p0 , при вычислениях может быть опущена,
так как она не дает вклада в вертикальную составляющую силы, а вклад в горизонтальную составляющую компенсируется силой от внешнего давления, действующей на правую половину шара. Тогда
π |
2r02 sin2 θ dθ = π r02 gρжh , |
|
||||
Fx = gρж ∫(h − r0 cos θ) |
(1.10.3) |
|||||
0 |
|
|
|
|
|
|
π |
|
|
|
|
|
|
Fz = −gmТ − gρж ∫(h − r0 cos θ) π r02 sin θ cos θ dθ = |
|
|||||
0 |
|
|
|
|
|
|
= − gm + |
|
2 |
π r3 gρ |
|
. |
(1.10.4) |
3 |
|
|||||
Т |
0 |
ж |
|
|
||
При вычислении вертикальной составляющей силы учтено, что на шар действует объемная сила, равная − gmт .
Шар вращаться не будет, так как поверхностные силы, действующие на любой элемент поверхности шара, направлены вдоль радиуса к центру шара. Результирующая объемных сил также приложена к центру шара.
1.11. В случае потери закрепления шар будет вытолкнут в горизонтальном направлении при условии равенства нулю горизонтальной составляющей результирующей силы, т.е. согласно (1.10.4)
при массе шара mТ = 23 π r03ρж .
1.12. В сферической системе координат уравнения движения невязкой жидкости (1.1) и (1.2) имеют вид:
∂∂ρτ + r12 ∂∂r (ρ r 2ur ) + r sin1 θ ∂∂ϕ (ρ uϕ) +
+ |
1 |
|
∂ |
(ρ uθ sin θ) = 0 , |
(1.12.1) |
|
r sin θ ∂θ |
||||||
|
|
|
||||
|
|
|
|
72 |
|
|

|
|
|
|
|
|
|
∂u |
r |
|
|
+ ur |
|
∂u |
r |
|
+ |
|
|
|
uϕ |
|
|
|
|
∂u |
r |
|
+ |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
∂τ |
|
|
|
|
∂r |
|
|
r |
|
sin θ ∂ϕ |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
+ |
|
u |
θ |
|
∂u |
r |
|
|
|
|
uϕ2 + uθ2 |
|
|
|
|
|
|
|
|
1 ∂p |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
= P |
− |
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||
|
r |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
ρ ∂r |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
∂θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vr |
|
|
|
|
|
|
|
|
|||||||||||||||
∂uϕ |
|
+ ur |
|
|
∂uϕ |
+ |
|
|
|
|
uϕ |
|
|
|
|
∂uϕ |
+ |
u |
θ |
|
|
∂uϕ |
+ |
||||||||||||||||||||||||
∂τ |
|
|
|
|
∂r |
|
r |
|
sin θ ∂ϕ |
|
r |
|
|
∂θ |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
_ |
uϕ ur |
|
+ |
uϕuθctgθ |
= P |
|
− |
|
1 |
|
|
|
|
∂p |
, |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ρ r ∂ϕ |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
Vϕ |
|
|
|
|
|
|
|
||||||||||||
∂u |
θ |
|
+ ur |
|
|
∂u |
θ |
|
+ |
|
|
|
uϕ |
|
|
|
|
∂u |
θ |
+ |
u |
θ |
|
|
∂u |
θ |
|
+ |
|||||||||||||||||||
∂τ |
|
|
|
|
∂r |
|
r |
|
sin θ ∂ϕ |
r |
|
|
∂θ |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
+ |
ur |
|
uθ |
− |
uϕ2ctgθ |
|
= P |
|
|
− |
|
1 |
∂p . |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
Vθ |
|
|
|
|
ρr ∂θ |
|
|||||||||||||||||
(1.12.2)
(1.12.3)
(1.12.4)
В соответствии с условиями задачи принимаем: ρ = const ,
PV = 0, uϕ = uθ = 0 и ur = ur (r, τ) . |
При этом система уравнений |
|||||||
движения упрощается |
|
∂ |
|
|
|
|
|
|
|
|
|
(r2ur ) = 0 , |
|
(1.12.5) |
|||
|
|
|
|
|
||||
|
|
∂r |
|
|
|
|||
|
∂ur |
|
+ ur |
∂ur |
= − |
1 ∂p . |
(1.12.6) |
|
|
∂τ |
|
∂r |
|||||
|
|
|
|
|
ρ ∂r |
|
||
Граничными условиями для компоненты скорости ur и давления р будут
|
dR(τ) |
& |
|
|
ur (r = R) = |
|
≡ R , |
(1.12.7) |
|
dτ |
||||
|
|
|
||
p(r = ∞) = p0 . |
(1.12.8) |
|||
Из уравнения неразрывности, которое упростилось к виду
(1.12.5), находим ur (r, τ) = Cr(2τ) . Используя для определения С( τ)
граничное условие (1.12.7), окончательно для распределения скорости имеем
73
|
R |
2 |
& |
|
|
ur (r, τ) = |
|
(τ)R(τ) |
. |
(1.12.9) |
|
|
|
|
|||
|
|
|
r2 |
|
|
Подставляя выражение для поля скорости (1.12.9) в (1.12.6) получим уравнение для определения давления, после интегрирования которого по радиусу в пределах от текущего r до бесконечности с учетом граничного условия (1.12.8) для распределения давления найдем
p(r, τ) − p0 |
&& 2 |
+ |
&2 |
|
&2 |
R |
4 |
|
|
|
= |
RR |
2RR |
− |
R |
|
. |
(1.12.10) |
|||
ρ |
|
r |
|
2 r4 |
||||||
|
|
|
|
|
|
|||||
Из (1.12.10) следует, что давление на поверхности расширяющейся сферы равно
&& |
& |
2 |
) . |
(1.12.11) |
p(r = R) = p0 + ρ(RR |
+1,5R |
|
1.13. Система уравнений движения жидкости, окружающей газовую полость, идентична рассмотренной в задаче 1.12. Справедлив и результат, полученный в 1.12, о зависимости давления на поверхности сферы (т.е. давления в газовой полости) от радиуса полости R(τ) (см. (1.12.11)). Обозначив через pг(τ) давление в газо-
вой |
полости и u(τ) |
– |
скорость |
движения |
поверхности сферы |
||||||
( u(τ) = R&(τ) ), соотношение (1.12.11) перепишем в виде |
|
||||||||||
|
|
R du |
+ |
3 |
u2 = |
1 ( pГ (τ) − p0 ) . |
(1.13.1) |
||||
|
|
|
|||||||||
|
|
dτ |
2 |
|
ρ |
|
|
||||
В |
соответствии |
с |
законом |
адиабатического |
расширения |
||||||
( pV γ = const ) давление в полости представим |
как функцию теку- |
||||||||||
щего радиуса полости R(τ) |
|
|
|
|
|
||||||
|
|
|
|
pг (τ) = |
pн( |
r0 |
)3γ . |
|
(1.13.2) |
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
R |
|
|
|
Подставляя выражение для pг(τ) в (1.13.1) и переходя от вре-
мени к новой независимой переменной R(τ) |
|
d |
= u |
d |
|
|
|
|
, получим |
||
|
|
||||
|
dτ |
|
dR |
||
уравнение для скорости на поверхности полости в зависимости от радиуса полости
74
|
d |
(R3u2 ) = |
2R2 |
|
r |
|
3γ |
|
|
|
|||||||
|
|
|
|
|
pн |
|
0 |
|
|
− p0 , |
(1.13.3) |
||||||
|
dR |
|
|
|
|
|
|||||||||||
|
|
|
|
ρ |
|
|
|
|
|
R |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которое просто интегрируется |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
R3u2 |
|
2R3 |
|
|
r |
3γ |
|
1 |
|
|
|
|
|||||
= |
|
− pн |
|
|
0 |
|
|
|
|
|
|
− p0 |
+ С . |
(1.13.4) |
|||
3ρ |
|
|
|
γ −1 |
|||||||||||||
|
|
|
|
|
|
R |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Константу интегрирования найдем, полагая, что в начальный момент R = r0 , а скорость u = 0 . Тогда
|
2 p |
н |
r |
3 |
|
r |
3(γ−1) |
|
|
2 p |
0 |
|
r |
3 |
|
|
|||
u2 = |
|
|
0 |
|
1 |
− |
0 |
|
|
+ |
|
|
|
0 |
|
−1 |
. (1.13.5) |
||
3ρ(γ −1) |
|
|
3ρ |
|
|||||||||||||||
|
|
R |
|
|
R |
|
|
|
|
R |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученное соотношение позволяет проанализировать поведение полости во времени. В начальный момент времени давление в
полости больше давления жидкости p0 , и полость будет расширяться. Первое слагаемое в (1.13.5) положительное и с ростом R(τ)
стремится к нулю, второе слагаемое отрицательно и при увеличении R(τ) стремиться к постоянному значению. Так как их сумма
должна все время оставаться положительной ( u2 ≥ 0 ), то размер полости R(τ) не может увеличиваться неограниченно. Существует
предельный размер полости Rmax , при котором рост полости прекращается, т.е. u2 становится равным нулю. Rmax является корнем (1.13.5) при u2 = 0 и определяется трансцендентным уравнением
|
|
|
3 |
|
pн |
|
|
|
r0 |
|
3(γ−1) |
|
|
|
|
|
|
|
|
|
|
||||||
|
Rmax |
|
|
|
|
|
|
|
|||||
|
|
|
|
=1 + |
|
|
1 |
− |
|
|
|
. |
(1.13.6) |
r |
|
(γ −1) p |
0 |
R |
|
||||||||
|
0 |
|
|
|
|
|
|
max |
|
|
|
||
В целом согласно (1.13.5) процесс представляется следующим образом. При расширении полости скорость ее роста u(τ) увеличи-
вается, достигает максимального значения и затем уменьшается. Рост полости прекращается, когда ее размер достигнет Rmax . К
этому моменту за счет сил инерции жидкости давление в полости станет меньше p0 , и после остановки полость начнет уменьшаться,
75
при этом u(τ) ≤ 0 . Согласно (1.13.5) сжатие полости будет продолжаться до тех пор, пока радиус полости не достигнет начального значения r0 , так как u2 (R = r0 ) = 0 . Затем полость снова начнет
расширяться. Ввиду отсутствия каких либо диссипативных процессов периодическое расширение и сжатие полости будет происходить неограниченно долго.
Максимальный размер, до которого расширяется полость, опре-
деляется параметром |
|
pн |
, и при его больших значениях, как |
|||
|
(γ −1) p0 |
|||||
следует из (1.13.6), равен |
|
|
|
|
||
|
|
|
|
pн |
13 |
|
|
|
|
|
|
(1.13.7) |
|
|
|
|
|
|||
|
Rmax ≈ r0 |
(γ −1) p0 |
. |
|||
|
|
|
|
|
|
|
1.14. Уравнение для потенциала поля скорости ϕ(r, θ) |
в безвих- |
|||||
ревом потоке невязкой жидкости, обтекающем цилиндр, имеет вид
1 ∂ |
r |
∂ϕ |
+ |
1 ∂2ϕ |
= 0 . |
(1.14.1) |
|||
|
|
|
|
|
|||||
r ∂r |
∂r |
r2 |
∂θ2 |
||||||
|
|
|
|
||||||
Его необходимо решить при условии непроницаемости поверхности цилиндра
∂ϕ |
|
= 0 |
(1.14.2) |
|
|||
∂r |
|
||
|
r =r |
|
|
|
0 |
|
|
и равенства скорости вдали от цилиндра скорости набегающего потока u0
∂ϕ |
|
|
|
|
= u0 cos θ, |
|
||
|
|
|||||||
∂r |
|
r →∞ |
|
|||||
|
|
|
|
|
||||
|
|
|
|
|
||||
1 ∂ϕ |
|
|
= −u0 sin θ . |
(1.14.3) |
||||
|
||||||||
r ∂θ |
|
r →∞ |
||||||
|
|
|
|
|
||||
|
|
|
|
|
||||
Решением задачи (1.14.1) – (1.13.3) является |
|
|||||||
|
|
|
|
|
|
r2 |
|
|
ϕ(r, θ) = u0 |
(r + |
0 |
) cos θ. |
(1.14.4) |
||||
|
||||||||
|
|
|
|
|
|
r |
|
|
Компоненты скорости при этом равны
76
|
r2 |
|
|
r2 |
|
|
|
ur (r, θ) = u0 (1− |
0 |
) cos θ, |
uθ(r, θ) = −u0 (1+ |
0 |
) sin θ . |
(1.14.5) |
|
r2 |
r2 |
||||||
|
|
|
|
|
Распределения давления в потоке определяется из уравнения
Бернулли |
|
|
|
|
|
|
|
|
|
|
|
|
|
p(r, θ) |
|
u2 |
(r, θ) + u2 |
(r, θ) |
|
p |
0 |
|
u2 |
|
|
|
|
+ |
r |
θ |
|
= |
|
+ |
0 |
. |
(1.14.6) |
|
|
ρ |
|
2 |
|
ρ |
2 |
||||||
|
|
|
|
|
|
|
|
|||||
Результирующая сила, действующая на цилиндр, равна нулю. 1.15. Разлагая вектор скорости на компоненты, и используя оп-
ределение потенциала скорости, получим |
|
|
|
|||||
|
∂ϕ |
= u0 nx , |
|
∂ϕ |
= u0 ny , |
∂ϕ |
= u0 nz , |
(1.15.1) |
|
|
|
|
∂z |
||||
|
∂x |
|
∂y |
|
|
|||
где nx = cos α, ny = cosβ, |
nz = cos γ – проекции единичного векто- |
|||||||
ра nr на оси координат, α, β, γ – направляющие углы вектора n . Из первого соотношения в (1.15.1) ϕ = u0 xnx + C1 ( y, z) , из второго следует, что C1( y, z) = u0 yny + C2 (z) , из третьего находим
C2 (z) = u0 znz + C3 . Окончательно |
|
ϕ(x, y, z) = u0 (xnx + yny + znz + C) . |
(1.15.2) |
1.16.ϕ(x, y) = u0 (xnx + yny + C1) , Ψ(x, y) = u0 ( ynx − xny + C2 ) .
1.17.При истечении жидкости из точки в окружающее пространство линии тока имеют вид лучей исходящих из этой точки, как показано на рис. О4.
При мощности источника Q радиальная
компонента скорости во всех точках поверхности сферы произвольного радиуса с центром в источнике равна
ur = |
Q |
. |
|
|||
4π r2 |
|
|||||
Так как |
|
|
||||
|
∂ϕ |
|
|
|
||
ur = |
|
, |
Рис. О4 |
|||
∂r |
||||||
|
|
|
|
|||
|
|
|
|
|
77 |
|
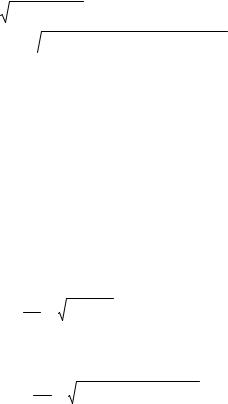
то для определения ϕ получаем уравнение |
∂ϕ |
= |
Q |
, после ин- |
|||
∂r |
4π r2 |
||||||
|
|
|
|
|
|||
тегрирования которого находим |
Q |
|
|
|
|
|
|
ϕ(x, y, z) = − |
. |
|
|
|
(1.17.1) |
||
4π r |
|
|
|
||||
|
|
|
|
|
|
||
Потенциал стока той же мощности отличается от (1.17.1) знаком. В (1.17.1) r – расстояние от источника (стока) до текущей
точки, равное r = x2 + y2 + z2 при расположении источника в
начале координат и r =  (x − x0 )2 + ( y − y0 )2 + (z − z0 )2 при расположении в произвольной точке ( x0 , y0 , z0 ).
(x − x0 )2 + ( y − y0 )2 + (z − z0 )2 при расположении в произвольной точке ( x0 , y0 , z0 ).
1.18. Поле скоростей линейного источника, действующего в начале координат
|
|
ur = |
V |
|
, uθ = 0 . |
|
|
|
|
|
|
(1.18.1) |
||||||
|
|
2π r |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В соответствии с определением потенциала и функции тока |
||||||||||||||||||
ur = |
∂ϕ |
= |
1 |
|
∂Ψ |
|
, uθ |
= 1 |
∂ϕ |
= − |
|
∂Ψ |
. |
(1.18.2) |
||||
∂r |
|
|
|
|
|
|
||||||||||||
|
|
r |
∂θ |
|
|
r ∂θ |
|
|
|
∂r |
|
|||||||
Из (1.18.1) и(1.18.2) находим |
|
|
|
|
|
|
V |
|
|
|
||||||||
ϕ(r, θ) = |
V |
ln r , |
Ψ(r, θ) = |
|
θ. |
(1.18.3) |
||||||||||||
|
|
|
|
|
|
2π |
|
|
|
|
|
2π |
|
|||||
В декартовой системе координат
ϕ(x, y) = V ln x2 |
+ y2 , |
Ψ(x, y) = |
|
V |
|
arctg |
y |
. |
||||
|
2π |
|
||||||||||
2π |
|
|
|
|
|
|
|
x |
||||
Для источника действующего в точке rr0 |
|
|
|
|
|
|
|
|||||
ϕ(x, y) = V ln (x − x )2 + ( y − y |
0 |
)2 , |
|
|
|
|||||||
2π |
|
0 |
|
|
|
|
|
|
|
|
||
|
|
y − y0 |
|
|
|
|
|
|
|
|
||
Ψ(x, y) = |
V |
|
arctg |
. |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
||||
|
|
x − x |
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
(1.18.4)
(1.18.5)
1.19. Поле скоростей плоского потенциального вихря с циркуляцией Γ
78
|
|
|
|
ur = 0 , |
|
uθ |
= |
|
Γ |
. |
|
|
|
|
|
|
|
|
|
|
(1.19.1) |
||||||||||
|
|
|
|
|
2π r |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В соответствии с определением потенциала и функции тока |
|||||||||||||||||||||||||||||||
ur = |
∂ϕ |
= 1 |
∂ϕ |
, |
|
uθ |
= 1 |
|
∂ϕ |
= − |
∂Ψ |
. |
(1.19.2) |
||||||||||||||||||
∂r |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
r ∂θ |
|
|
|
|
|
r ∂θ |
|
|
|
|
∂r |
|
|
|
|
||||||||||||||
Из (1.19.1) и(1.19.2) находим |
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
||||||||||||||
|
ϕ(r, θ) = |
|
Γ |
|
θ, |
Ψ(r, θ) = − |
|
|
ln r . |
(1.19.3) |
|||||||||||||||||||||
2π |
2π |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В декартовой системе координат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ϕ(x, y) = |
Γ |
arctg |
y |
, |
Ψ(x, y) = − |
|
Γ ln |
|
x2 |
+ y2 . |
(1.19.4) |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
2π |
|
x |
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|||||||||
Для источника действующего в точке rr0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
ϕ(x, y) = |
|
|
Γ |
arctg |
y − y0 |
|
, |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Ψ(x, y) = − Γ ln |
(x − x )2 |
|
+ ( y − y |
0 |
)2 . |
(1.19.5) |
|||||||||||||||||||||||||
|
|
|
|
|
2π |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.20.ϕ = ax , Ψ = ay , ux = a , uy = 0 .
1.21.Представив в выражении для комплексного потенциала
Φ = u |
∞ |
(z + r2 |
z) |
комплексную |
переменную |
в |
виде |
|
0 |
|
|
|
|
|
z = r exp(iθ) ≡ r(cos θ + i sin θ) , и имея в виду, что Φ = ϕ + iΨ , для потенциала и функции тока в цилиндрических координатах найдем
ϕ = u |
∞ |
(r + r2 |
r) cos θ, |
Ψ = u |
∞ |
(r − r2 |
r) sin θ. (1.21.1) |
|
0 |
|
|
0 |
|
||
Компоненты скорости при этом равны |
|
|
|||||
|
r2 |
|
|
r2 |
|
|
ur (r, θ) = u∞ (1 − |
0 |
) cos θ, |
uθ(r, θ) = −u∞ (1 + |
0 |
) sin θ. (1.21.2) |
|
r2 |
r2 |
|||||
|
|
|
|
Из (1.21.1) и (1.21.2) следует, что цилиндрическая поверхность
r = r0 непроницаема |
для |
потока |
жидкости ( Ψ(r = r0 ) = 0, |
|
ur (r = r0 ) = 0 ), скорость |
обтекания |
поверхности |
цилиндра |
|
uθ(r = r0 ) = −2u∞ sin θ . |
Вдали от цилиндра (при r → ∞) |
скорость |
||
везде постоянна и равна u∞ . Таким образом, мы имеем случай обтекания цилиндра радиусом r0 потоком со скоростью u∞ .
79
1.22. Представляя в выражении Φ(z) = czn |
комплексную пере- |
|||
менную |
z = x +iy в виде z = r exp(iθ) , |
где r = x2 + y2 , |
||
θ = arctg |
y |
, и имея в виду, что Φ = ϕ + iΨ , для потенциала скоро- |
||
x |
||||
|
|
|
||
сти и функции тока в цилиндрической системе координат получим
ϕ = crn cos(nθ) , |
Ψ = crn sin(nθ) . |
(1.22.1) |
Компоненты скорости при этом равны |
|
|
ur = cnrn−1 cos(nθ) , |
uθ = −cnrn−1 sin(nθ) . |
(1.22.2) |
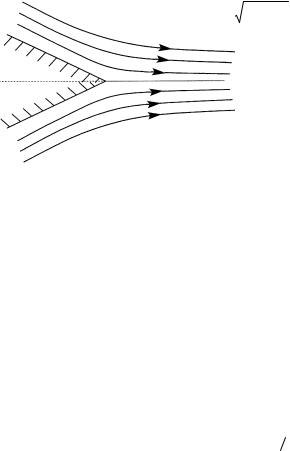
Согласно (1.22.1) линия тока, соответствующая значению Ψ = 0 , совпадает с направлениями осей θ = 0 и θ = ±π n (рис. О5).
n (рис. О5).
Рис. О5
Вдоль этих линий тока нормальная к ним компонента скорости uθ равна нулю, а радиальная изменяется по закону ur = cnrn−1
вдоль радиуса θ = 0 и ur = −cnrn−1 |
вдоль |
радиусов θ = ±π n |
(1.22.2). Направление движения жидкости показано на рис. О5. Ли- |
||
нии тока, соответствующие значениям |
Ψ ≥ 0 |
лежат выше луча |
θ = 0 , Ψ ≤ 0 ниже. |
|
|
Если изменить знак в выражении для комплексного потенциала, то направление движения вдоль линий тока изменится на противо-
положное, т.е. комплексный потенциал Φ(z) = −czn описывает обтекание потоком жидкости клина с углом раствора θк = 2π(1 −1 n) , так как n ≥ 0 скорость в лобовой точке клина ( r = 0 ) равна нулю.
n) , так как n ≥ 0 скорость в лобовой точке клина ( r = 0 ) равна нулю.
80
