Р а б о т а 16 изучение pp-рассеяния при энергии протонов 660 МэВ

Цель – определение полного _полн и неупругого _неупр сечений рассеяния протона на протоне при энергии налетающего протона T_p = 660 МэВ.

ВВЕДЕНИЕ

В результате взаимодействия частиц происходят разнообразные процессы их превращений. Реакции взаимодействия двух частиц a и b можно разделить на упругие, квазиупругие и неупругие. Под реакцией упругого рассеяния подразумевается процесс взаимодействия (a + b  a + b), в котором сорт частиц не изменяется, а изменяются лишь их импульсы. В процессе квазиупругого взаимодействия частиц a и b в конечном состоянии образуются так же, как и при упругом рассеянии, две частицы, но их сорт отличается от сорта частиц a и b (a + b  c + d). Самую большую группу процессов образуют реакции неупругого взаимодействия (a + b  c + d + ...), в результате которых образуется более двух частиц. Количественной мерой процессов взаимодействия частиц является сечение. Оно характеризует число соответствующих реакций, происходящих в единицу времени в единице объема при единичной плотности потока падающих частиц и единичной плотности частиц мишени. Это определение относится к лабораторной системе координат, но само понятие сечения является релятивистским инвариантом.

Дифференциальное сечение процесса взаимодействия частиц a и b c образованием произвольного числа вторичных частиц с импульсом в интервале от до подсчитывается по формуле [5]

. (16.1)

Здесь S_i:(S_a, S_b); S_f – спиновые квантовые числа первичных и вторичных частиц; |M|² – квадрат модуля инвариантной амплитуды процесса, которая усредняется по спиновым состояниям первичных частиц и суммируется по спиновым состояниям вторичных частиц, после чего зависит только от кинематических переменных. Величина j называется инвариантным потоком и равна [(P_aP_b)² – m_a²  m_b²]^1/2; где P_a, P_b – 4-импульсы первичных частиц a, b; – сумма 4-импульсов вторичных частиц,E_f – полная энергия вторичной частицы. В формуле (16.1) выражение

есть элемент фазового объёма вторичных частиц.

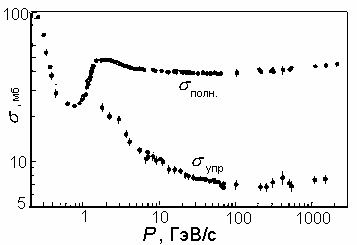
Рис. 16.1

Как видно из рис. 16.1, сечение упругого рр-рассеяния уменьшается с увеличением энергии налетающего протона, а полное сечение, начиная с энергии E_p  500 МэВ, практически остается постоянным. С ростом энергии (при E_p > 300 МэВ) в рр-рассеяние включаются неупругие каналы с рождением одного, двух и т.д. -ме­зонов и других частиц.

Кинематический анализ упругого рассеяния протонов при больших энергиях позволяет получить формулу, дающую связь между углами, под которыми вылетают рассеянный протон (угол ) и протон отдачи (угол ):

ctg  ctg = 1 + T_p/(2M_pc²), (16.2)

где T_p, M_p – кинетическая энергия и масса налетающего протона. Из этой формулы следует, что угол разлёта двух протонов ( + ) в отличие от нерелятивистского случая (ctg  ctg = 1) меняется в пределах

( + )_мин  ( + )  /2.

Величина ( + )_мин является функцией энергии протона T_p, достигается при  =  и определяется формулой

. (16.3)

Напомним, что в нерелятивистском случае  +  = /2.

Более подробно поведение сечения рассматривается в [6]. Используя импульсную диаграмму упругого рассеяния протона на протоне при больших энергиях, можно убедиться в правильности формулы (16.3).

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Рассеяние протонов на протонах изучалось с помощью пузырьковой камеры, облученной пучком протонов синхроциклотрона ОИЯИ в г. Дубне. Схема установки показана на рис. 16.2, а.

а)

б)

Рис. 16.2

На рис. 16.2, б приведены вид сбоку на пузырьковую камеру и расположение оптических систем для фотосъемки. Камера наполнена жидким водородом, плотность которого составляла 0,058 г/см³, и помещена в магнитное поле напряженностью Н = = 12000 Э. События в камере фотографировались двумя фотоаппаратами, что давало возможность при изучении снимков восстановить их пространственную картину.

Для выполнения работы студентам предлагаются экспонированные пленки. Просмотр пленок проводится с помощью фотоувеличителя, к которому прилагается транспортир для измерения углов. На пленках зафиксированы следы протонного пучка, V-образные события, соответствующие актам рассеяния на водороде, и следы -электронов. В отличие от протонов следы -электронов сильно искривлены магнитным полем.

Рис. 16.3

Одно и то же событие в камере представлено на пленке на двух кадрах, смещенных друг относительно друга на 5 кадров (рис. 16.3).

На одном из парных кадров ставится на пленке порядковый номер. Кроме того, на каждом кадре имеются визирные метки +, нанесенные на переднее стекло пузырьковой камеры, и Х – на заднее стекло. Справа на нумерованном кадре и слева от парного ему кадра имеются белые кресты на черном фоне, отмечающие положение оптических осей фотообъективов Z, Z.

Все эти метки необходимы для восстановления пространственной картины и проверки компланарности следов частиц. Восстановление проводится следующим образом. При заданном увеличении картина рассеяния переносится с нумерованного кадра на бумагу. Здесь же отмечаются визирные метки на переднем стекле и правая оптическая ось.

Затем, передвигая пленку, находят парный кадр и, совмещая его визирные метки с нанесенными ранее на бумагу, отмечают левую оптическую ось. Снова переносят на бумагу картину события. Оба изображения будут смещены относительно друг друга. Изображение каждой точки смещается параллельно линии, соединяющей точки Z и Z (положение оптических осей). По смещению характерных точек следов – «параллаксу» (например, а а и т.д.), используя известные данные по геометрии опыта, можно найти глубину каждой точки в камере. Причем за окончательное изображение данной точки принимается не ее положение на снимках, а точка, полученная пересечением лучей, проведенных из оптических центров к изображениям этой точки на снимках (рис. 16.4, б).

Рис. 16.4

Зависимость глубины точки в камере от параллакса ее изображений при заданном увеличении представлена на графике (рис. 16.5).

Рис. 16.5

После определения глубины характерных точек a,b,c,dследabпродолжается до пересечения с линией, соединяющей точкиcиd(см. рис. 16.4,б). В случае компланарности всех следов точка О будет истинным пересечением прямыхabиcd, в противном случае линииabиcdбудут скрещиваться, но не пересекаться. Проверить это можно, определив отдельно глубину точки О, лежащей на прямыхabиcd. Если эти глубины окажутся одинаковыми, то прямыеabиcdдействительно пересекаются. Для этого на любой прямой (как это показано на рис. 16.4,а) отмечаются расстояния между точкамиc, О,d, затем из каждой точки восстанавливаются перпендикуляры и на них откладываются отрезки, соответствующие известной глубине точекcиdв камере. Прямая линия, проведенная через концы этих отрезков, отсечет на перпендикуляре, восстановленном из точки О, отрезок, соответствующий глубине точки О, лежащей на прямойcd. Аналогично находится глубина точки О, лежащей на прямойab. Сравнивая глубину точки О, найденную двумя путями, делаем заключение о принадлежности данного события к упругому (компланарному) или неупругому (не компланарному)рр-рассеянию. В последнем случае процесс сопровождается вылетом одной нейтральной частицы. Вероятность вылета двух нейтральных частиц существенно меньше.

Компланарность упругого и некомпланарность неупругого рассеяния следует из закона сохранения импульса. Неупругий процесс может дать компланарную картину только в тех редких случаях, когда третья нейтральная частица вылетела в одной плоскости с двумя протонами. Вероятность такого события будет тем меньше, чем точнее проверяется компланарность. В качестве дополнительного критерия для отделения случаев упругого рр-рассеяния от неупругого может служить угол разлета частиц. По двум проекциям угла восстанавливается истинный угол разлета частиц в пространстве. Если этот угол окажется > 90, то случай рассеяния является неупругим процессом. Рассеяние будет также неупругим, если угол разлета меньше минимального угла для упругого рассеяния, который всегда однозначно определен для заданной энергии падающих протонов. Если падающие частицы имеют разброс по энергиям, то минимальный угол рассчитывается по максимальной энергии протонов в падающем пучке. В промежуточной области углов возможно и упругое, и неупругое рр-рассеяние. В этой области компланарность является единственным критерием, применяемым для отделения случаев упругого рассеяния от неупругого.

Угол рассеяния в пространстве (истинный угол рассеяния) определяется следующим образом. На картине события, аналогичного представленному на рис. 16.4, измеряется угол ₁, затем находится угол наклона данного трека к переднему стеклу камеры по соотношению tg₁ = Z/L, где L – истинная длина данного трека в камере от его начала до характерной точки, т.е. длина bc; Z – разница глубин точек b и с (истинный диаметр камеры 12,6 см). Тогда угол рассеяния в пространстве ₁ находится по формуле cos₁ = = cos₁  cos₁.

Зная истинные углы рассеяния для всех найденных случаев рр-рассеяния, можно построить распределение этих событий по углам и вычислить угловую зависимость дифференциальных сечений упругого и неупругого рр-рассеяния. Полные сечения упругого и неупругого рассеяния находятся интегрированием полученных угловых распределений с учетом тождественности взаимодействующих частиц.

В настоящей работе измеряются только плоские углы на нумерованных кадрах для всех случаев рр-рассеяния (как упругого, так и неупругого). Затем строится зависимость дифференциальных сечений рр-расcеяния от этих плоских углов. Зная число актов взаимодействия в мишени N, сечение можно определить по формуле

N = N₀  (1 – exp(–n    х)), (16.4)

где N₀ – число падающих протонов, n – число ядер в 1 см³ мишени,  – сечение данного процесса, х – толщина мишени. В нашем случае жидководородной мишени толщиной 12,6 см величина n    х << 1, поэтому мишень можно считать тонкой и проводить расчет по формуле N = N₀  n    х. Тогда  = N/N₀  n  x. Потери энергии налетающих протонов на ионизацию в камере не меняют существенно их энергию.

Дифференциальное сечение в заданном интервале углов получается следующим образом. Определяют среднюю загрузку кадра первичными протонами, затем по количеству просмотренных нумерованных кадров на пленке получают полное число падающих первичных протонов N₀. В выбранном интервале плоских углов подсчитывают число случаев рассеяния N в интервале . Плоский угол  – это коническая проекция угла рассеяния на плоскость пленки. Поэтому построенные дифференциальные сечения являются проинтегрированными по всем истинным углам рассеяния, дающим одну и ту же проекцию на плоскость пленки. В нашей работе интервалы  равны 10.

Дифференциальное сечение в выбранном интервале углов рассчитывается по формуле:

, (16.5)

где  – эффективная толщина мишени, соответствующая рабочей области, в которой можно измерить углы рассеяния. Обычно  < x (в данной работе   11 см). Остальные обозначения определены выше.

Рис. 16.6

На рис. 16.6 приведен график зависимости дифференциального сечения упругого рр-рассеяния от плоских углов, построенный на том же экспериментальном материале. Поэтому после построения суммарной гистограммы для упругого и неупругого дифферен­циальных сечений можно вычесть из нее графически гистограмму для упругого процесса и выделить часть, относящуюся к неупругим событиям. Графическое интегрирование гистограмм дифференциальных сечений упругого и неупругого рр-рассеяния позволяет получить значения полных сечений этих процессов при энергии падающих протонов 660 МэВ.

Как показала практика, основная погрешность получаемых результатов есть субъективная ошибка, состоящая в пропуске случаев рр-рассеяния при просмотре пленки. Она доходит до 4050 %. Следующей по величине погрешностью является статистическая, которая составляет 30 % для полного сечения. Остальные погрешности существенно меньше указанных выше.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Вставить пленку в кассету фотоувеличителя. Установить увеличение проектора в соответствии с прилагаемой картинкой шаблона и в дальнейшем его не менять.

2. Для каждого случая рр-рассеяния измерить на нумерованных кадрах углы между направлением первичного и рассеянных протонов. Просмотреть всю пленку (25 м). Необходимо фиксировать все случаи рр-рассеяния, которые произошли в эффективном объеме камеры. Это те события, для которых можно с достаточной точностью измерить углы рассеяния.

3. Зарисовать два случая рассеяния (по указанию преподавателя), совмещая для каждого случая оба кадра по визирным меткам. Отметить также оптические оси обоих фотообъективов.

4. Определить среднюю загрузку кадра протонами и записать полное число просмотренных нумерованных кадров.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Построить угловую зависимость дифференциальных сечений.

2. Используя приведенную кривую для упругого рассеяния (см. рис. 16.6), выделить часть, относящуюся к неупругим процессам.

3. Определить полное сечение упругого и неупругого рр-рассеяний. Учесть, что число углов в два раза больше, чем число актов рассеяния.

4. Для зарисованных случаев проверить компланарность и определить истинные углы рассеяния.

5. Вычислить минимальный угол разлета протонов при упругом взаимодействии протона с кинетической энергией 660 МэВ с покоящимся протоном.

6. Используя то, что выражение Е² – Р²с², является релятивистки инвариантным, вычислить пороговую энергию для рождения одного и двух -мезонов для случаев неупругого рр-соударения.