
Климанов Сборник задач по теории переноса, дозиметрии и засчите 2011
.pdf
Министерство образования и науки Российской Федерации
Национальный исследовательский ядерный университет «МИФИ»
Сборник задач по теории переноса, дозиметрии и защите от ионизирующих излучений
Под редакцией В.А. Климанова
Рекомендовано УМО «Ядерные физика и технологии» в качестве учебного пособия для студентов высших учебных заведений
Москва 2011
УДК 539.1.07(076) ББК 31.42я7 С23
Сборник задач по теории переноса, дозиметрии и защите от ионизирующих излучений: Учебное пособие / А.А. Званцев,
В.А. Климанов, А.И. Ксенофонтов, Н.Н. Могиленец, М.П. Панин, В.В. Смирнов; под ред. В.А. Климанова. М.: НИЯУ МИФИ, 2011. 196 с.
В книге представлены задачи по четырем дисциплинам, изучаемым студентами НИЯУ МИФИ по специальности «Радиационная безопасность человека и окружающей среды»: «Введение в теорию переноса ионизирующих излучений», «Численные методы теории переноса ионизирующих излучений», «Дозиметрия ионизирующих излучений» и «Защита от ионизирующих излучений». Задачи распределены по трем главам, каждая глава разделяется на тематические разделы. В начале каждого раздела дается краткое изложение теории и основные формулы, необходимые для решения задач. В конце книге приводятся ответы к задачам и в приложении содержатся дополнительные справочные материалы.
Книга написана преподавателями кафедры «Радиационная физика и безопасность атомных технологий» НИЯУ МИФИ, имеющими большой опыт в преподавании этих четырех курсов, Книга предназначена для студентов, преподавателей и аспирантов инженерно-физических и физико-технических вузов, специализирующихся в области радиационной физики и радиационной безопасности, а также для слушателей курсов повышения квалификации.
Пособие подготовлено в рамках Программы создания и развития НИЯУ МИФИ.
Рецензент д-р физ.-мат. наук, проф. В.Т. Самосадный
ISBN 978-5-7262-1487-0
©Национальный исследовательский ядерный университет «МИФИ», 2011
|
Оглавление |
|
Предисловие………………………………………….. |
5 |
|
Глава 1. Теория переноса ионизирующих |
|
|
излучений……………………………………………………... |
7 |
|
1.Характеристики поля излучений. Взаимодействие |
|
|
излучения с веществом…………………………… |
7 |
|
2. |
Уравнения переноса для нейтронов и фотонов |
|
Аналитические методы решения……………………. |
19 |
|
3. |
Численные детерминистские методы……………. |
34 |
4. |
Метод Монте-Карло…………………………………. |
38 |
Глава 2. Дозиметрия ионизирующих излучений………….. 54
5. |
Основные дозирметрические величины…………… |
54 |
|
6. |
Ионизационный метод дозиметрии………………… |
59 |
|
7. |
Дозиметрия фотонов и β-частиц………………… |
65 |
|
8. |
Энергетическая зависимость чувствительности |
|
|
(ЭЗЧ) дозиметров в полях фотонного излучения…… |
70 |
||
9. |
Сцинтилляторы в дозиметрии ионизирующих |
|
|
излучений……………………………………………. |
73 |
||
10. |
Интегрирющие дозиметры………………………… |
76 |
|
11. |
Дозиметрия излучений инкорпорированных |
|
|
нуклидов……………………………………………… |
82 |
||
12. |
Оценка погрешностей дозиметрических |
|
|
величин………………………………………………. |
87 |
||
13. |
Некоторые полезные соотношения……………… |
89 |
|
14. |
Задачи для решения в вычислительной системе |
|
|
Mathcad.......................................................................... |
92 |
||
Глава 3. Защита от ионизирующих излучений |
99 |
||
15. |
Радиационные характеристики источников |
99 |
|
излучения……………………………………………….. |
|
||
16. |
Радиационная безопасность……………………….. |
105 |
|
17. |
Методы расчета защиты от гамма-излучения |
113 |
|
18.Защита от нейтронов…………………………………. 118
19.Альбедо излучений…………………………………… 126
20.Защита от α и β-излучения…………………………… 133
3
Приложение (Справочный материал)………………………. 136
Ответы и указания |
169 |
Список литературы…………………………………………… 187
4
Предисловие
Почти двадцать лет прошло после последнего (четвертого) издания книги «Сборник задач по дозиметрии и защите от ионизирующих излучений» (авторами 4-го издания были В.И. Иванов, В.А. Климанов, В.П. Машкович). Задачник за эти годы стал основным учебным пособием для семинарских и практических занятий у студентов в России, обучающихся по специальности «Радиационная безопасность человека и окружающей среды». Однако с течением времени вследствие физического износа и других естественных причин книга стала практически библиографической редкостью. Вместе с тем простое переиздание задачника было бы нецелесообразным, так как за эти годы нормирование радиационной безопасности в России претерпело существенное изменение, была разработана и реализована на практике новая концепция эффективной дозы, появилось много новых рекомендаций международных и национальной организаций, связанных с регулированием и обеспечением радиационной безопасности. Важно также, что в настоящее время происходит переход обучения на двухуровневую систему бакалавр-магистр и на образовательные стандарты третьего поколения, что также требует создания новой учебной литературы.
Данные причины обусловили издание новой книги, предназначенной для семинарских и практических занятий по нескольким дисциплинам, входящим в Государственный образовательный стандарт специальности «Радиационная безопасность человека и окружающей среды». К этим дисциплинам относятся: «Введение в теорию переноса ионизирующих излучений», «Численные методы теории переноса», «Дозиметрия ионизирующих излучений» и «Защита от ионизирующих излучений».
К нашему глубокому сожалению, заведующий кафедрой «Радиационная физика, биофизика и экология» МИФИ (теперь кафедра «Радиационная физика и безопасность атомных технологий» НИЯУ МИФИ) профессор В.И. Иванов и профессор В.П. Машкович преждевременно ушли из жизни. Авторы настоящего пособия - преподаватели той же кафедры, они многие годы работали под руководством и совместно с В.И. Ивановым и В.П. Машковичем, некоторые из них являются их учениками, и все имеют большой опыт преподавания указанных выше дисциплин. Поэтому в книге сохранены методические принципы, структура и стиль изложения материала. Задачник по-прежнему состоит из трех глав, каждая из которых содержит несколько тематических разделов. В начале всех раз-
5
делов даются краткое изложение теории и основные формулы, необходимые для решения задач. Вместе с тем изменено название задачника, что более точно отвечает содержанию книги. В первой главе появилось значительное количество новых задач, тексты оставшихся же, учитывая опыт преподавания, пересмотрены. В остальных главах учебного пособия все задачи являются новыми.
В первую главу, авторами которой являются профессор В.А. Климанов и доцент М.П. Панин, вошли задачи по теории переноса ионизирующих излучений. В ней приведены задачи по определению основных характеристик поля излучения, по расчету сечений взаимодействия ионизирующих излучений с веществом, получению различных форм и аналитических решений уравнения переноса в приближениях элементарной теории диффузии, элементарной теории замедления, теории возраста, по методу последовательных столкновений и получению численных решений уравнения переноса детерминистскими методами и методом Монте-Карло.
Вторая глава - доцент В.В. Смирнов и ст. преподаватель Н.Н. Могиленец - посвящена дозиметрии ионизирующих излучений. Она содержит задачи по расчетам и оценкам основных физических процессов взаимодействия излучений с веществом, обусловливающих передачу и поглощение энергии в различных средах, по методикам установления связей измеренных различными детекторами величин с соответствующими дозиметрическими величинами, по расчетным методам определения параметров дозных полей для частиц различного вида, по оценкам погрешностей дозиметрических величин. Представлен ряд задач дозиметрии, решаемых в рамках вычислительной системы Mathcad.
Третья глава - доцент А.И.Ксенофонтов и ст. преподаватель А.А. Званцев - посвящена защите от ионизирующих излучений. В эту главу включены следующие разделы: расчет защиты от фотонов, нейтронов, заряженных частиц и от смешанного излучения, радиационная безопасность и альбедо излучений.
Авторы
6
ГЛАВА 1. Теория переноса ионизирующих излучений
1.Характеристики поля излучения. Взаимодействие излучения
свеществом
Наиболее полная информация о стационарном поле ионизирующего излучения задается пространственной энергетически-угловой
плотностью потока частиц ϕ(r, E,Ω) . Эта величина представляет
собой отнесенное к единичному энергетическому интервалу число частиц с энергией E, движущихся в направлении единичного векто-
ра Ωв единичном телесном угле и пересекающих за единицу времени помещенную в точке r пространства единичную площадку,
нормаль к которой по направлению совпадает с вектором Ω.
1. Пространственная энергетически-угловая плотность тока час-
тиц J (r, E,Ω) совпадает по модулю с ϕ E,Ω) |
но в отличие от |
|
ϕ(r , E,Ω) является вектором, совпадающим(r , |
по, |
направлению с |
вектором Ω: |
|
|
J (r , E,Ω) = Ω ϕ(r, E,Ω). |
|
(1.1) |
2. На практике часто интересуются переносом частиц не через поверхность, положение которой строго определенным образом
фиксируется вектором Ω, а через поверхность, произвольным образом ориентированную в пространстве. Такая задача эквивалентна
определению скалярной величины Jk (r , E,Ω) – проекции тока из-
лучения на направление, задаваемое вектором k , – скалярного тока.
Пространственная энергетически-угловая плотность скалярного тока частиц Jk( r ,E, Ω) через произвольным образом ориентированную единичную площадку Sk ( k – нормаль к площадке Sk) является проекцией J (r, E,Ω) на направление, задаваемое вектором k :
Jk(r, E, Ω) = ( J (r, E,Ω) k ) = ( Ω, k )· ϕ(r , E,Ω) =
= φ( r ,E, Ω) ·cos( Ω, k ). |
(1.2) |
3. Интегрированием функции ϕ(r , E,Ω) по энергетической или угловой переменной получают пространственно-угловую ϕ(r ,Ω)
7
или пространственно-энергетическую φ( r ,E) плотность потока частиц. Пространственное распределение плотности потока частиц (или интегральная плотность потока частиц) φ(r) представляет со-
бой интеграл от ϕ(r ,Ω) или φ( r ,E) по угловой или энергетической переменной. Аналогичное интегрирование можно выполнить с функциями J (r, E,Ω) и Jk (r , E,Ω) . При этом интегральная плот-
ность скалярного тока частиц |
|
Jk (r ) = (J (r ), k ) = ∫Jk (r, E,Ω) dΩ . |
(1.3) |
представляет собой число частиц, пересекающих в единицу времени произвольным образом ориентированную единичную площадку
Sk.
Нередко используемые на практике парциальные плотности потока и тока φ+, φ-, Jk+ , Jk− определяются интегрированием соответ-
ствующих дифференциальных характеристик по положительной или отрицательной полусфере направлений.
4. Микроскопическое интегральное сечение взаимодействия на один атом определяется как отношение
σ =ν /(ϕ na ), |
(1.4) |
где ν – число ионизирующих частиц, испытавших взаимодействие в единицу времени с na атомами, находящимися в поле излучения
с плотностью потока φ.
Дифференциальное энергетически-угловое (или дважды дифференциальное) микроскопическое сечение рассеяния
σ(E′ → E,Ω′ → Ω) численно равно вероятности ионизирующей
частице рассеяться на единице пути в веществе, имеющем один атом в единице объема, так, что при этом энергия частицы изменит-
ся с E' на E и направление движения – с Ω′ на Ω в единичных интервалах вокруг E и Ω. Для азимутально-симметричного рассеяния
σs (E′ → E,Ω → Ω) = σs (E′ → E,(Ω′,Ω)) = σs (E′ → E,cosθs ). (1.5)
Макроскопические сечения равняются соответствующим микро-
скопическим сечениям, умноженным на число атомов na в единице объема.
5. Дифференциальное сечение комптоновского рассеяния фотона на свободном электроне равно:
8
σ (α,μ ) = |
r02 |
|
|
1 |
|
|
1+μ2 |
+ |
α2 (1-μS )2 |
, |
(1.6) |
||||
|
[ |
|
S |
] |
|
||||||||||
k |
s |
2 |
|
|
S |
1+α(1-μ |
|
|
|
|
|||||
1 |
+ α(1-μ ) |
2 |
|
S |
) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
где α = E/0,511; r0 – классический радиус электрона; μs – косинус угла рассеяния θs; r02 / 2 = 3,92 10−26 см2.
Энергия фотона после комптоновского рассеяния определяется по формуле
E′ = |
E |
(1.7) |
1+ E(1−μS )/ 0,511. |
Энергия нейтрона после рассеяния на угол θс в системе центра инерции
E′ = 0,5E (1+ α) + (1−α)cosθc |
1+b |
+ |
A |
|
Q, |
(1.8) |
|
A +1 |
|||||||
|
|
|
|
|
|||
где α = (A-1)2/(A+1)2; b = Q(A+1)/(AE); Q – энергия, идущая на воз-
буждение ядра.
Связь между косинусами углов рассеяния нейтрона в лабораторной системе координат μS и в системе центра инерции μс определяется следующей формулой:
μS = |
γ+μc |
, |
(1.9) |
|
1+2γμc +γ2 |
||||
|
|
|
где γ =1/ A2 + A( A +1)Q .
E
Задачи
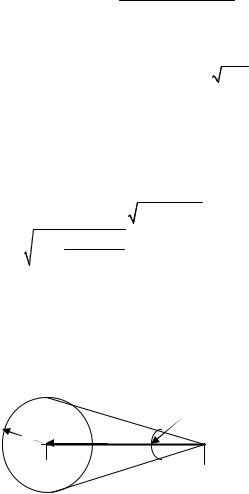
1.1. Определить телесный угол ΔΩ, под которым виден диск радиусом R из точки D, расположенной на оси диска на расстоянии h от него (рис. 1.1). К какой величине стремится ΔΩ при h→0 или при
R→∞?
R
ΔΩ
 D
D
h
Рис. 1.1. Геометрия задачи 1.1
9
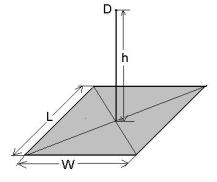
1.2. Определить телесный угол ΔΩ, под которым видна прямоугольная площадка W×L из точки D, расположенной на перпендикуляре, восстановленном из геометрического центра площадки, на расстоянии h от площадки (рис. 1.2).
Рис. 1.2. Геометрия задачи 1.2
1.3. Направляющий вектор Ω обычно выражают в сферической системе координат. Считая эти координаты заданными, выразить
Ωв декартовой системе и цилиндрической системах координат.
1.4.Показать, что φ( r ) численно равна длине пути, проходимой
вединицу времени частицами в элементарном объеме, находящем-
ся вблизи точки r , деленной на величину элементарного объема. 1.5. Докажите эквивалентность трех следующих определений
флюенса частиц в точке r :
а) Φ = lim( N / A) при V → 0,
где N – число частиц, проникающих в объем элементарной сферы с площадью поперечного сечения A, расположенной вокруг точки r ;
б) Φ = lim(∑di / V ) при V→ 0,
i
где di – сегмент трека i-частицы, укладывающийся внутри объема
V;
∞∞
в) Φ = ∫dt∫dE ∫dΩ ϕ(r, E.Ω,t).
00 4π
1.6.Пусть в заданной точке пространства r угловая плотность потока частиц изотропна, т.е. описывается выражением
10
