ВОКС_2013 / Лекция 3

Лекция 3. Полное внутреннее отражение. Лучевое уравнение.

Из курса общей физики известно, что на границе раздела двух оптических сред имеет место эффект, называемый преломление света. Уравнение, описывающее преломление света при прохождении через оптические среды с различным показателем преломления были выведены Голландским астрономом и математиком Вилбродом ван Ройен Снеллем

Рис. 3.1.

(Willebrod van Roijen Snell). Если , - показатели преломления сред, и - углы падения и преломления относительно нормали, то справедливо отношение:

(3.1)

Отношение (3.1) можно также представить в виде:

(3.2)

Формулы (3.1), (3.2) можно представить и иначе. Если рассматривать угол падения не относительно нормали, а относительно самой поверхности (углы , ), то, учитывая, что

, ,

а также, что

, (*)

получаем:

При увеличении угла падения , если луч переходит из среды с большим показателем преломления в среду с меньшим показателем преломления (), то при некотором значении угла , величина угла достигнет . (т.е. далее увеличиваться уже не сможет). При углах падения больше указанного все излучение отражается обратно в среду с показателем преломления . Этот эффект называется эффектом полного внутреннего отражения, а угол при котором возникает указанный эффект – критическим углом. Из (3.1) следует, принимая во внимание, что , следует:

() (3.3)

Точно такой же эффект имеет место и распространении излучения в волоконном световоде. Если представить ВС в виде диэлектрического прозрачного цилиндра с сердцевиной с показателем преломления определенного диаметра и бесконечной оболочки с показателем преломления , то для лучей, распространяющихся таким образом, что они пересекают ось ВС, также будет справедливо соотношение (3.2). Реально, не может быть бесконечно большой оболочки и не расходящихся световых пучков, однако если толщина оболочки и диаметр светового пучка (луча) существенно больше длины волны излучения, а диаметр сердцевины существенно больше диаметра пучка, рассматриваемая модель, называемая лучевой моделью, позволяет объяснить основные закономерности распространения излучения в ВС. Достоинства и недостатки лучевой модели будут рассмотрены позже. Лучи, которые пересекают ось ВС, называются меридиональными. Лучи, которые не пересекают ось ВС, называются косыми или немеридиональными.

В ВС излучение, а в данном случае рассматриваемые лучи, попадают через входной торец, на поверхности которого они испытывают преломление.

Рис. 3.2.

Если при падении луча относительно оси ВС под углом угол меньше критического, излучение, введенное в световод, далее будет распространяться в нем за счет эффекта полного внутреннего отражения. Вычислим угол , при котором угол в ВС равен критическому углу и обозначим его .

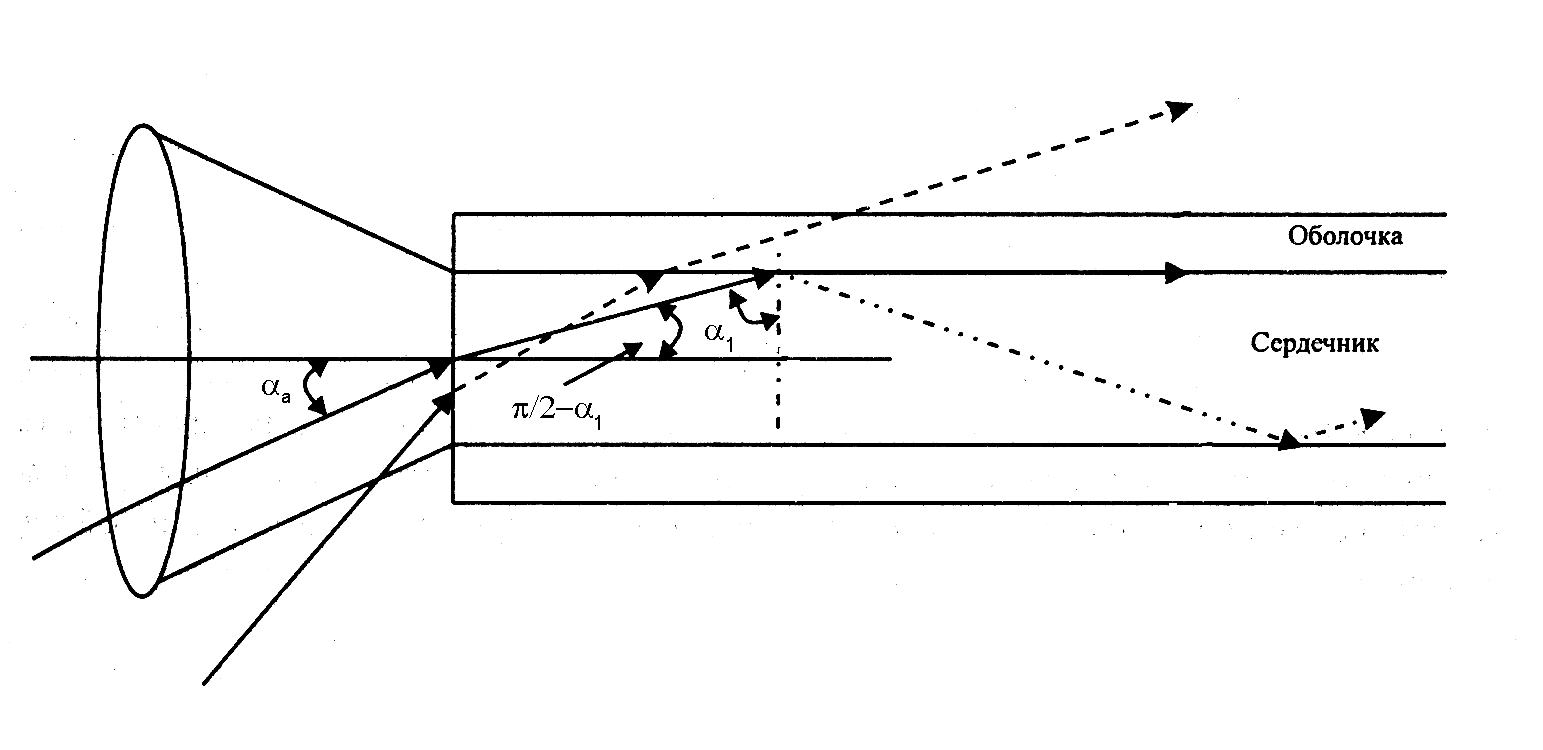
Рис. 3.3.

Так как

,

учитывая (*) и полагая , имеем:

Принимая во внимание, что , т.е. . При получаем:

С учетом (3.3):

(3.4)

Эта величина называется числовой апертурой (сокращенно «ЧА» или “N.A.”), а угол - апертурным углом.

Теперь более точно сформулируем определение введенного термина. Апертура – действующее отверстие оптического прибора. Угловая апертура – угол между крайними лучами конического светового пучка, входящего в оптическую систему. Часто угловую апертуру называют апертурным углом. Числовая апертура – синус апертурного угла. Для рассматриваемого случая – идеализированного ВС со ступенчатым профилем показателя преломления (ППП), числовая апертура (ЧА) определяется выражением (3.4).

Если стыковать без фокусирующей системы ВС и источник излучения с широкой диаграммой направленности, то при одинаковых диаметрах сердцевины, чем больше ЧА световода, тем больше вводится в него излучения от источника.

Типичные значения ЧА для световодов из стекла – 0,15 … 0,25 (стандарт – 0,22), с сердцевиной из стекла, оболочной из полимерного материала – 0,2…0,4, полимерного ВС – до 0,5.

Теперь представим, что свет проходит не одну границу раздела сред, а несколько (в общем случае - слоев).

Рис. 3.4.

Вначале луч переходит из среды с ППП равным в среду с ППП , далее – с и т.д. Положим, что . Тогда , т.е. по мере прохождения слоев угол луча относительно нормали увеличивается, соответственно, относительно поверхности – уменьшается. Возможно, что угол относительно поверхности станет меньше критического, возникнет эффект полного внутреннего отражения и луч изменит направление движения. Такой луч, в конце концов, вернется в среду с ППП равным .

Теоретически, уменьшая толщину слоев, можно перейти от дискретного изменения показателя преломления между слоями к непрерывной функции – профилю показателя преломления.

В общем случае для описания траектории луча в пространстве с градиентом ППП существует, так называемое, лучевое уравнение или уравнение эйконала:

(3.6)

где - пространственная зависимость ППП. Рассмотрим частный случай.

Рис. 3.6.

Тогда (3.6) можно представить в виде:

, (3.7)

(3.8)

Так как, в этом случае:

, (3.9)

. (3.10)

Интегрируя (3.8), получаем:

(3.11)

Уравнение (3.11) называют обобщением закона Снелля для градиентных сред. Из (3.11) можно вычислить максимальное значение координаты , достигаемого лучом с начальным углом . В точке поворота луча . Тогда:

(3.12)

Рис. 3.7.

Прямая, соответствующая уравнению , разграничивает две области: в одной из них луч находится постоянно () и область, в которую луч никогда не попадает (). Множество точек поворота луча с одинаковыми значениями начального угла распространения называется лучевой каустикой. Иногда вместо термина «множество точек» используется термин «геометрическое место точек». А также лучевую каустику иногда называют «каустикой точек поворота».

Если бы среда была бы бесконечна по координате , то для любого угла нашлась бы точка поворота . Но среда не может быть бесконечной хотя бы потому, что должно быть не меньше единицы. А если среда с зависимостью ограничена в пространстве по координате (зависимость выполняется только при ), что имеет место в реальных случаях, возникает ограничение на максимальное значение начального угла при котором имеет место поворот луча. Очевидно, что таким условием является .

Рис. 3.8.

Если , а , то (3.12) можно записать в виде . Откуда получаем:

(3.13)

По аналогии со случаем ступенчатого ППП угол будем назвать критическим, и введем аналогичное обозначение - . Таким образом, лучи с начальным углом распространения и далее распространяются в среде, причем , а при в процессе распространения имеет место и луч выходит из среды с зависимостью . Для первого случая () лучи называются направляемыми (направляемые лучи), для второго - рефрагируемыми (рефрагирующие лучи).

Формула (3.13) определяет критический угол в точке . При показ. Преломления среды меньше, чем при , соответственно, меньше и максимальный угол , при котором наблюдается поворот лучей. Поэтому вводят термин «локальный критический угол скольжения», т.е. это , что можно также обозначить как . Аналогично (3.13):

Все то, что сказано выше о распространении луча в градиентной среде, можно применить и к оптическим световода с градиентным ППП. Аналогично случаю ступенчатого ППП, это относится к меридиональным лучам. Также аналогично случаю распространения лучей в ВС со ступенчатым ППП в ВС могут распространяться, так называемые, косые лучи. Для рассмотрения более общего случая - определения траектории движения произвольных лучей в градиентом ВС необходимо использовать лучевое уравнение в цилиндрической системе координат. Решение такого уравнения, естественно, сложнее, чем для случая плоской поверхности. Метод решения представлен, в частности, в [Х.Г. Унгер]. Сущность решения такова, что не только меридиональные, но и косые лучи при распространении по ВС могут иметь точку поворота и, соответственно, могут распространяться по световоду. Если изобразить проекции траекторий движения косых лучей на плоскость торца, то они будут иметь следующий вид:

Рис. 3.9

То есть, для трехмерного случая, проекция траектории световых пучков на плоскость, перпендикулярную оси ВС, имеет более сложный вид, чем зависимости, рассмотренные выше. Однако все указанные ранее закономерности, как для ВС со ступенчатым профилем показателя преломления, так и для градиентного ВС, сохраняются.

Мы рассмотрели эффект полного внутреннего отражения с точки зрения лучевой или геометрической оптики. При более строгом рассмотрении с использованием волнового уравнения эффект полного внутреннего отражения можно описать более точно. Отличия более точного расчета от простейшей лучевой модели заключается в следующем.

1. Электромагнитное поле проникает в среду с меньшим показателем преломления. Причем чем больше угол падения отличается от критического, тем больше глубина проникновения.

2. Если от границы раздела сред отражается световой пучок, ограниченный в пространстве, то имеет место смещение центра пучка. Этот эффект называется смещением Гооса-Генхена.

Рис. 3.10.

Необходимо отметить, что при переходе от рассмотрения распространения луча в слоистой среде со скачкообразным (ступенчатым) изменением ПП к распространению луча в среде с непрерывным изменением ПП возникает противоречие, вызванное неточностью используемой физической модели. Исходя из лучевого уравнения, а также для модели со ступенчатым изменением ПП в слоях при распространении луча возможно возникновение точки поворота, что также подтверждается экспериментальными исследованиями. А в среде с непрерывным изменением ПП при достижении угла нулевого распространения луча относительно выбранной оси в точке поворота, в направлении дальнейшего движения луча имеет место . Поэтому в этой точке дальнейшее движение луча нельзя рассматривать как преломление на границе двух сред. А если говорить про лучевую теорию вообще, то она неприменима для определения пространственного распределения интенсивности вблизи каустики.

Применения лучевой теории для описания свойств волоконных световодов также имеет определенные ограничения, которые будет рассмотрены ниже (более подробно обсуждаться ниже).

9