ВОКС_2013 / Лекция 5

Лекция 5. Характеристическое уравнение. Волноводные моды.

Ранее было показано, что в связи с необходимостью выполнения условия непрерывности тангенциальных компонент э/м поля на границе раздела сердцевины и оболочки, в световоде могут распространяться э/м волны только с определенными параметрами, соответствующие решениям характеристического уравнения:

(5.1)

где

(5.2)

(5.3)

, (5.4)

Величины и связаны соотношением:

(5.5)

Решения данного уравнения для переменной называют собственными числами характеристического уравнения. Собственное число зависит от величины параметра называемого азимутальным индексом. Для каждого азимутального индекса может быть большое количество решений. Поэтому собственные числа номеруют, начиная с меньшего значения. Соответственно, собственные числа имеют два индекса: азимутальный и так называемый радиальный, соответствующий номеру корня (например ). Количество корней характеристического уравнения зависит от величины нормированной частоты. Далее будет показано, что собственные числа для различных типов волн различны. Из формул (5.2)-(5.4) следует, что . Режим распространения волн при называют «вдали от отсечки» (“far from cutoff”), а - «вблизи отсечки» (“near cutoff”).

Волны (или моды), соответствующие решениям уравнения (1), кроме случая называются гибридными модами. При уравнение (1) переходит в два независимых уравнения:

для (5.6)

для (5.7)

Э/м волны, соответствующие решениям уравнения (5.6) называют TE_0j модами и они описывают случай . Э/м волны, соответствующие решениям уравнения (5.7) называют TM_0j модами и они описывают случай . TE_0j и TM_0j моды называют также поперечными волнами. Иногда их также называют H_oj и E_0j волнами.

Вначале рассмотрим решения уравнений (5.6), (5.7). Используем выражения для производных бесселевых функций:

,

и асимптотические выражения для отношения функций Макдональда при (т.е. при условии «вдали от отсечки»):

Тогда уравнения (5.6), (5.7) можно записать в виде:

(5.8)

(5.9)

Графическое решение уравнений (5.8), (5.9) представлено на рис. 5.1.

Рис. 5.1.

Введем точки являющиеся -тым корнем уравнения .

Понятно, что решения следует искать вблизи точек , являющихся решениями уравнения

. (5.10)

Корни уравнения (5.10) можно рассматривать как нулевое приближение решений уравнений (5.6), (5.7). Следует отметить, что для многих прикладных задач большая точность не требуется. При необходимости, увеличить точность определения корней характеристического уравнения для поперечных волн можно, применив линейную аппроксимацию отношения вблизи точек и положив (т.е. рассматривая случай . Такой способ решения называется методом линеаризации. Тогда:

для TE_0s (5.11)

для TM_0s (5.12)

Откуда получаем:

для TE_0s (5.13)

для TM_0s (5.14)

где . Формулы (5.13), (5.14) целесообразно использовать в тех случаях, когда необходимо определить разность собственных чисел или постоянных распространения TE_0j и TM_0j мод. Для практического использования удобным является применение асимптотических формул для вычисления нулей функций Бесселя. В этом случае:

для TE_0s (5.15)

для TM_0s (5.16)

Решение уравнения (1) при несколько сложнее и требует отдельного рассмотрения входящих в его состав функций. Представим у-е (1), помножив левую и правую часть уравнения на , в виде:

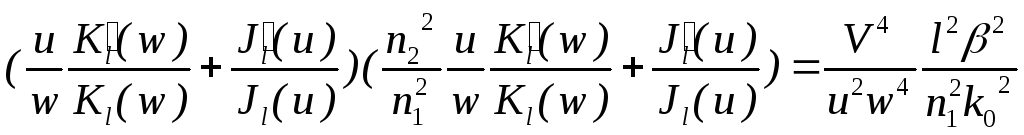(5.17)

Пусть:

(5.18)

(5.19)

(5.20)

Соответственно, уравнение (5.17) переходит в уравнение:

(5.21)

Графики функций , и для многомодового режима распространения излучения в световоде () представлены на рис.

Функции , от при =100, =1.45, , .

Графическое решение характеристического уравнения (5.21) приведено на рис.

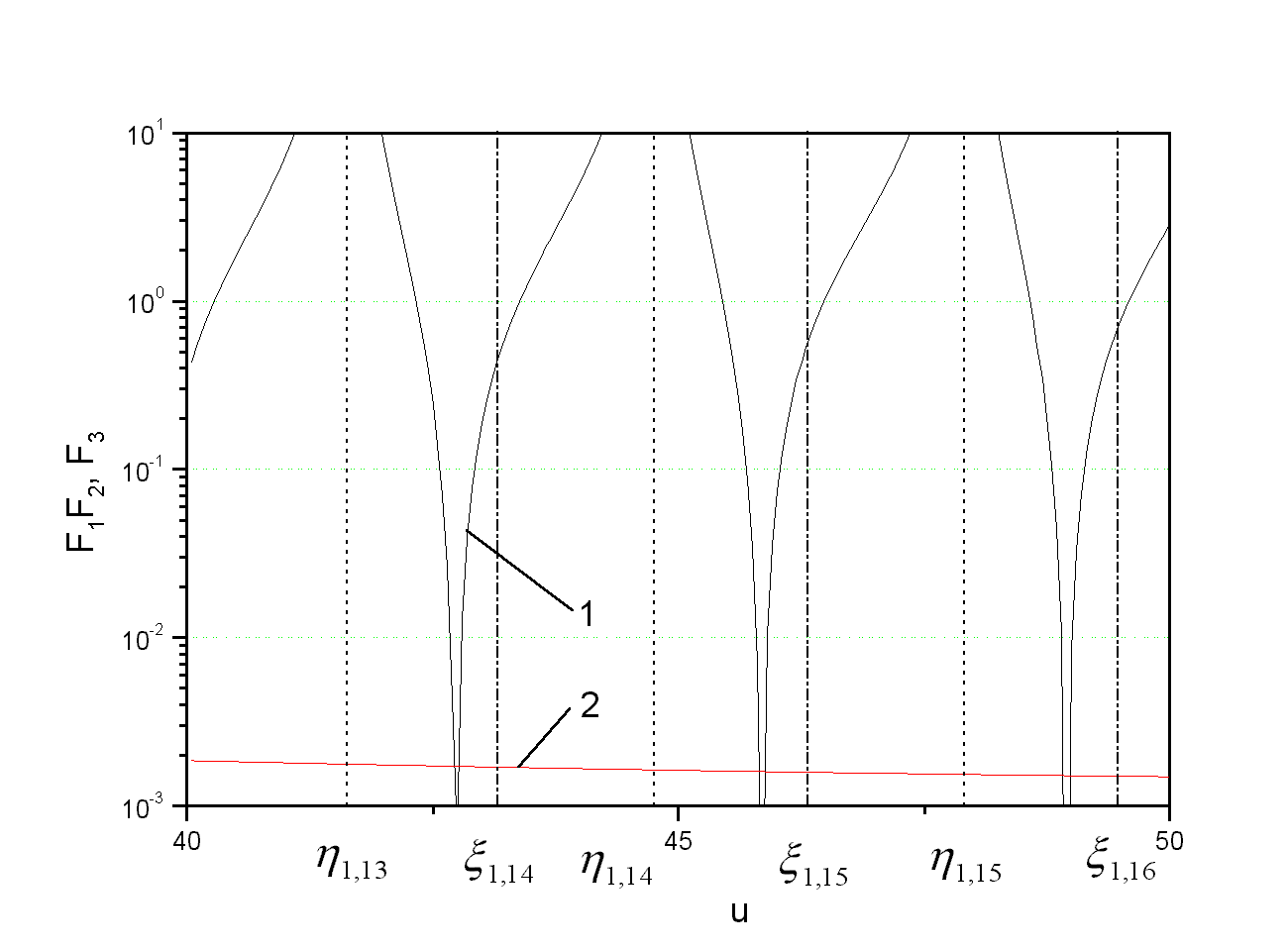
Графическое решение характеристического уравнения .

Введем обозначения точек и , которые будут решениями уравнений:

для (5.22)

для (5.23)

Из рис. … следует:

1. в интервалах при ( - целое число) существуют два корня уравнения. Обозначим корни уравнения как и . Причем .

2. в интервалах существуют только одно решение - .

3. решения для собственных чисел и 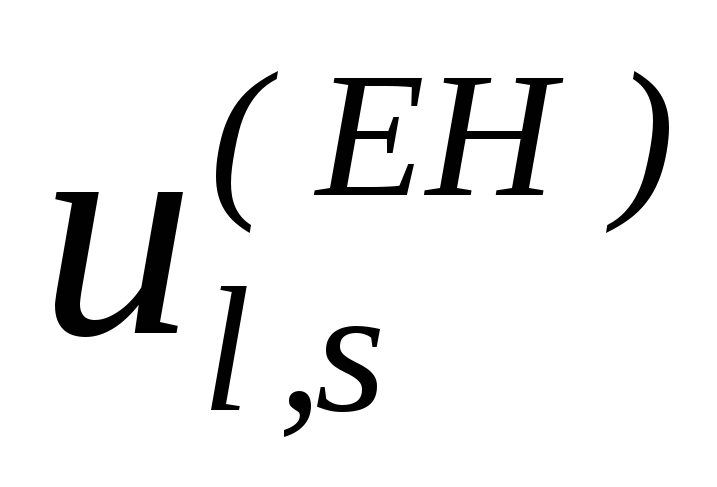следует искать вблизи точек .

4. для каждой модовой группы существует своя предельная величина нормированной частоты , при меньших значениях которой распространение мод, входящих в данную модовую группу, невозможно. Эту величину называют нормированной частотой отсечки модовой группы.

Моды, имеющие собственные числа и называются и модами соответственно. Однако чаще всего корни уравнения нумеруют не по номеру интервала между корнями уравнения (5.22), а в порядке номеров, начиная от 1. Поэтому собственным числам и соответствуют и моды. Во многих случаях и собственные числа нумеруют аналогично нумерации мод.

Известно, что для бесселевых функции справедливы следующие рекуррентные формулы (формула дифференцирования):

(5.24)

При :

или (5.25)

Нулевым приближением для вычисления собственных чисел гибридных мод считаются решения уравнений:

для и (5.26)

для мод. (5.27)

Обозначим решения уравнений (5.26) и (5.27) как . Для конечного значения можно использовать следующее приближение:

(5.28)

Формула (5.26)-(5.28) называют асимптотическими, так в основу этих формул положено асимптотическое поведение бесселевых функций и характеристического уравнения. Существуют и другие асимптотические формулы и методы решения характеристического (дисперсионного) уравнения. В многомодовом режиме обще число мод оценивается по формуле:

(5.29)

Одно из наиболее важных свойств характеристического уравнения заключается в том, что все волноводные моды кроме моды имеют определенную нормированную частоту отсечки. Мода теоретически может распространяться в световоде при любом значении . Это означает, что при уменьшении радиуса сердцевины световода или при увеличении длины волны излучения по мере уменьшения происходит уменьшение количества распространяющихся в световоде мод. При некотором значении в световоде остается только одна волноводная мода. Такой режим распространения называется одномодовым, а световоды, в которых при заданной длине волны распространяется только одна мода – называются одномодовыми. Условием одномодового режима распространения волн в световоде со ступенчатым профилем показателя преломления является:

где - первый корень функции Бесселя нулевого порядка, т.е.

. (5.30)

Вычисление корней характеристического уравнения вблизи отсечки других волноводных мод отличается от ранее представленного подхода для случая «вдали от отсечки» (формулы (5.26), (5.27)). Для условия отсечки определяются из уравнения .

В световодах с иным ППП, например, с параболическим или треугольным ППП, характеристическое уравнение также иное. Однако общим свойством является наличие минимального значения нормированной частоты при котором достигается одномодовый режим, так называемой частоты отсечки. Нормированная частота отсечки зависит от ППП. Если величину обозначить как , то нормированная частота отсечки для световодов со степенным законом изменения ППП ( - показатель степени) справедливо следующее приближение:

, (5.31)

где - относительный показатель преломления. Для ВС с параболическим ППП (=2) . Обычно, световоды изготавливают с такими параметрами, чтобы они являлись одномодовыми на длине волны более 1.3 мкм. Типичные значения: =4.5 мкм, - от 0.03 до 0.04.

Электромагнитные поля волноводных мод световода со ступенчатым профилем показателя преломления

Ранее были рассмотрены формулы, позволяющие описать напряженность электрического и магнитного поля волноводных мод. Рассмотрим эти решения подробно. Ранее принято, что решения уравнений Максвелла для волноводных мод можно представить в виде:

, (5.32)

, (5.33)

т.е. в виде произведения радиальной и азимутальной зависимостей, причем обе зависимости могут быть представлены как действительные функциями от действительных аргументов (исключая волны, называемые оптическими вихрями). Комплексной функцией комплексного аргумента является функция , определяющей фазу волнового процесса. При использовании метода комплексных амплитуд, после того как определены производные полей по времени (), фазовый множитель не рассматривается. Для проекций векторов электрического и магнитного поля в цилиндрической системе координат можно записать:

(5.34)

(5.35)

(5.36)

(5.37)

(5.38)

(5.39)

где - произвольный угол, определяющий фазу азимутальной зависимости. Радиальные зависимости и проекций в общем случае различные. Следует отметить, что зависимости (5.34)-(5.39) являются либо действительными, либо мнимыми. При фазовом множителе выражения для полей и являются действительными, а поперечных полей – мнимыми.

Из выражений (5.34)-(5.39) следует:

1. пространственное положение узлов и пучностей поля как по радиусу, так и по азимуту не зависит от времени. То есть, по радиусу и по азимуту волна является стоячей.

2. Для проекций поля как в сердцевине ВС, так и в оболочке выполняется отношение: .

3. Азимутальные зависимости напряженности электрического и магнитного поля смещены по фазе азимутальной зависимости на угол .

4. Все компоненты э/м поля содержат множитель, описываемый тригонометрической функции синуса или косинуса с аргументом вида , где - фазовый множитель.

Часто в литературе рассматривают отдельно два типа волн – с азимутальной зависимостью, описываемой функцией косинуса и функцией синуса. Линейной комбинацией этих двух функций можно получить волну с произвольной азимутальной фазой . Поэтому далее можно рассмотреть параметры э/м поля только одной из этих мод, а параметры поля второй - получить поворотом осей координат на угол равный . Соответственно, для моды с произвольной величиной угла - поворотом на угол .

Физический смысл индексов волноводных мод: азимутальный индекс характеризует количество узлов азимутальной зависимости продольных составляющих э/м поля ( и ). Количество узлов равно , например, при =1 поле имеет 2 азимутальных узла. Радиальный индекс также характеризует количество узлов и пучностей. Но количество пучностей о диапазоне радиусов равно радиальному индексу, а количество узлов – может быть на один меньше. Рассмотрим несколько примеров.

1. Напряженности электрического и магнитного полей , .

Рис.

Теперь рассмотрим моды.

Рис.

Например, при радиальная зависимость модуля напряженности поля имеет два максимума. Минимумов – тоже два, но один из них – на границе сердцевины и оболочки нельзя считать узлом.

Важным свойством мод является линейная поляризация мод , в частности, моды , называемой основной.

В световоде со ступенчатым профилем показателя преломления выражения для напряженности э/м поля могут быть представлены в виде:

(5.32)

(5.33)

Условие соответствует точкам в оболочке световода, т.е. формулы (5.32), (5.33) описывают напряженность э/м как в сердцевине, так и в оболочке ВС. Хорошо известно, а также следует из формул (5.32), (5.33), что э/м поле приникает в оболочку с меньшим показателем преломления. Используя уравнения Максвелла можно вычислить все остальные компоненты э/м поля. В волоконной оптике введено понятие «размер пятна моды» или «радиус модового поля», который применяется для случая одномодового режима распространения излучения. Для этого используют аппроксимацию распределения напряженности поля на выходном торце световода функцией Гаусса:

(5.34)

где - размер пятна моды. Для ВС с гауссовским распределением ППП выражение (5.35) является решение волнового уравнения для , , , компонент. Независимо от ППП радиус пятна моды больше радиуса сердцевины световода. Существует приближенная формула для определения радиуса модового поля при условии :

(5.35)

Известно, что при в сердцевине ВС распространяется 75% энергии моды, при это значение уменьшается до 20%. Затухание излучение в оболочке ВС обычно существенно больше, чем в сердцевине, кроме того, световод, в котором значительная часть излучение распространяется в оболочке имеет существенно большие потенри на изгибах. Поэтому одномодовые ВС разрабатываются таким образом, чтобы в рабочем диапазоне длин волн нормированная частота находилась в пределах .

Рис.

Для одномодовых ВС со ступенчатым ППП существует простое приближение, позволяющее вычислить радиус модового поля при :

(5.36)

В гауссовом приближении поле основной моды можно описать выражениями:

поляризация вдоль оси	поляризация вдоль оси

То есть, поле основной моды можно аппроксимировать полем плоской волны с гауссовским радиальным распределением напряженности. Соответственно, проекциями векторов напряженности электромагнитного поля – пренебречь.

14