Идентификация нелинейных систем

Существует несколько методов идентификации нелинейных систем:

1. Метод прямого поиска;

2. Аппроксимация нелинейности;

3. Модель Гаммерштейна;

4. Метод Виннера;

5. Двухэтапная процедура.

Метод прямого поиска

Нелинейную функцию f(x) преобразуют в линейную функцию f_л(x) . Далее применяют любой метод идентификации линейных систем.

Допустим, что модель объекта имеет вид:

,

где х₁, х₂ – входные параметры, у – выходной параметр, а₀, в₁, в₂ – искомые параметры.

Рассматриваем только положительные значения у.

Аппроксимация нелинейности

Таблично заданная функция (явно нелинейная) аппроксимируется с помощью полинома произвольным методом. Полученный полином и есть модель нашего объекта.

Ограничения: функция должна быть непрерывна.

Существует теорема Вейерштрасса, которая доказывает, что все нелинейности можно описать полиномом:

а) Замена линейной переменной и сведение к регрессии;

б) Применение интегральных формул.

Модель Гаммерштейна

Входной сигнал u(t) известен.

1. Если известна функциональная зависимость f(u(t)) – вид нелинейности, то вводим Z=f(u(t)). Идентификация сводится к определению параметров линейной части:

.

2. Функциональная зависимость f(u(t)) не известна. Строится таблица этой нелинейной зависимости. По этой таблице любой интерпретируемой формулой получаем аппроксимирующий полином нелинейности f^*(u(t)). Зная параметры аппроксимирующего полинома, вводим Z(t) = f^*(u(t)) и, снимая соответствующие ему y(t), решаем задачу идентификации:

.

Пример: Система приводится к следующему виду:

Р

ис. 22 Схема нелинейной системы

- функция является нелинейной.

Используя метод интерполяции, аппроксимируем полином

Составляем обобщенный вектор:

Тогда искомая матрица:

может быть получена по выражению:

,

где

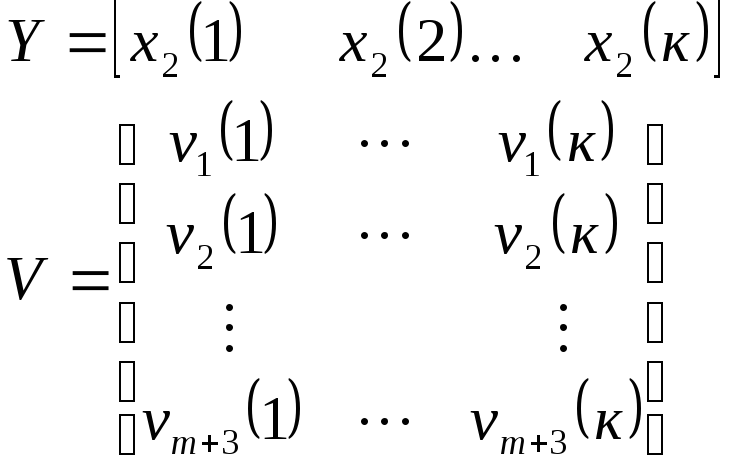
Метод Виннера

Является наиболее точным методом идентификации, на практике применяется крайне редко из-за сложности вычислений и отсутствия ясной физической интерпретации.

Двухэтапная процедура

1. Нелинейная характеристика разбивается на участки, в пределах которых нелинейная функция может быть с достаточной долей точности представлена линейной функцией. Данные участки называются участками линеаризации. Начало участков называется точкой линеаризации. В каждой точке линеаризации входной переменной придается незначительное приращение и фиксируется изменение выходной переменной. По данным входного и выходного переходного процесса с помощью линейных методов идентификации строятся линейные модели.

2. Аппроксимация линейных моделей в нелинейную функцию.

На основе зарегистрированного переходного процесса строится матрица коэффициентов линейным реверсионным методом. В результате получим столько матриц, сколько узловых точек. Каждый коэффициент матрицы аппроксимируется по той или иной интерполяционной формуле с помощью любого полинома.

Пример: Рассматривается отдельно нелинейное звено. На нелинейной характеристике выбирается отрезок, где система ведет себя как линейная функция.

Р

ис. 23 График нелинейной функции

Отрезок, где функция линейна - , гдеx₁ⁱ – точки или узлы линеаризации.

Для точек линеаризации подбираем соответствующие входные точки

.

Каждой точке линеаризации подаем входную переменную, увеличивающуюся на величину

.

Снимаем переходный процесс системы для каждой точки линеаризации.

Для каждой точки линеаризации получаем линейную модель А_i

По каждому a_ij получаем функциональную зависимость a_ij = f(a_ij) методом аппроксимации тем же самым полиномом

.
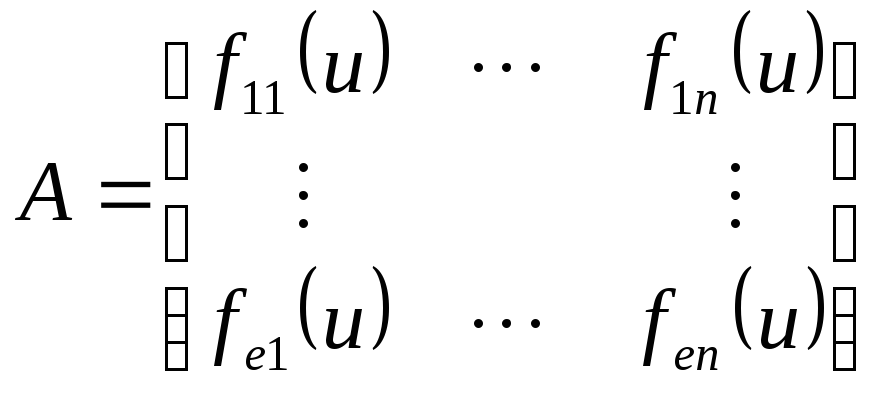