Работа 3.12

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПРИЗМЫ И ДИФРАКЦИОННОЙ РЕШЕТКИ

Н.Г.Захаров

А.В.Головин л.П.Круковская

ЗАДАЧА

1.Исследовать дисперсионные свойства призмы при падении на нее лучей под углом наименьшего отклонения. Определить угловую дисперсию и разрешающую способность призмы.

2.Исследовать дисперсионные свойства отражательной дифракционной решетки. Определить постоянную решетки, угловую дисперсию и разрешающую способность.

ВВЕДЕНИЕ

Для работы спектральных приборов (спектрометров, монохроматоров) необходимо осуществить пространственное разложение сложного излучения по длинам волн. Это разложение осуществляется диспергирующими элементами – оптическими призмами и дифракционными решетками.

а) ПРИЗМА. Разложение света трехгранной призмой объясняется зависимостью показателя преломленияnматериала призмы от длины волны излучения. Для определения угла отклонения рассмотрим ход лучей через призму (рис.1). Запишем закон преломления света на двух гранях призмы:

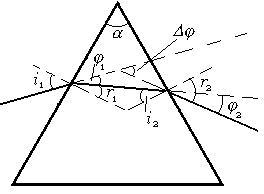
Рис.1

.

Соотношения между углами падения, преломления и отклонения:

₁=i₁-r₁, ₂=i₂-r₂, = r₁+i₂.

Угол называется преломляющим углом призмы. Обычно его величина около 60^о. Угол отклонения:

i₁+r₂. (1)

Т.о. полный угол отклонения луча зависит от угла падения луча на первую грань, угла преломления на второй грани и преломляющего угла призмы. Зависимость угла r₂ от показателя преломления приводит к тому, что углы отклонения лучей разных длин волн оказываются различными, что приводит к пространственному разделению света по длинам волн. Анализ функции(i₁) на экстремум показывает, что эта функция имеет минимум при некотором значении угла i₁=i_m,называемом углом наименьшего отклонения:

(2)

На практике призму стараются расположить под углом наименьшего отклонения. Формула (2) позволяет определить показатель преломления:

(3)

Рис. 2

б) ДИСПЕРСИОННАЯ КРИВАЯ ПРИЗМЫ.Используя формулу (3), можно получить дисперсионную кривую призмы,т.е. зависимость n() (по известному значению  и измеренным для разных длин волн углам отклонения). Величина dn/d называется дисперсией призмы – она различна для разных спектральных участков.

в) РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ СПЕКТРАЛЬНОГО ПРИБОРА. Допустим, мы освещаем входную щель спектрального прибора светом, содержащим две монохроматические линии  и +, спектральный прибор дает изображение линий в виде двух полос конечной ширины (рис.2а). Не всякие две линии могут быть разрешены, т.е. видны раздельно. На рис.2а и 2б линии разрешены, 2в не разрешены. Согласно критерию Релея, линии называются разрешенными, если минимум одной совпадает с максимумом другой (рис.2б).

Величина R=/ называется разрешающей способностью. Расчеты показывают, что для призмы R зависит от ширины пучка света, освещающего призму и наклона дисперсионной кривой (рис.3).

(4)

Рис.3

УГЛОВАЯ ДИСПЕРСИЯ определяется угловым расстоянием между двумя спектральными линиями, отнесенными к разности длин волн:

Угловая дисперсия различна для различных участков спектра, поэтому для расчетов D_ следует выбрать близко расположенные линии.

ДИФРАКЦИОННАЯ РЕШЕТКА. Оптическая дифракционная решетка представляет собой стеклянную пластинку, на которую с помощью специальной делительной машины нанесен ряд параллельных штрихов. Дифракционные решетки могут быть прозрачными и отражательными. В первом случае ряд прозрачных участков разделен рядом непрозрачных, во втором случае решетка имеет особый профиль (рис.4) и отражающей является лишь часть поверхности. В нашей работе использована отражательная решетка.

Рис.4

При взаимодействии световых волн с дифракционной решеткой имеют место дифракционные явления, заключающиеся в том, что часть энергии светового излучения распространяется в направлении, отличном от первоначального (для прозрачной решетки) или от направления зеркального отражения (для отражательной) и перераспределяется главным образом в определенных направлениях – направлениях на дифракционные максимумы. Дифракционный максимум имеет место тогда, когда разность хода лучей, идущих от соседних щелей, равна

=1-2=d(sin-sin)=k (5)

Величина d носит название постоянной решетки.  - угол падения,  - угол дифракции, k=1, 2, 3, … - число, называемое порядком дифракции.

Из (5) видно, что угол дифракции, определяющий направление, в котором наблюдается дифракционный максимум, зависит от , т.е. дифракционная решетка является диспергирующим элементом. Число наблюдаемых спектров определяет параметр k – порядок дифракции. В направлении зеркального отражения =, k=0, разложения в спектр нет, это так называемый спектр нулевого порядка.

РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ДИФРАКЦИОННОЙ РЕШЕТКИ:

(6)

где N – число штрихов, k – порядок дифракции. В случае решетки большая разрешающая способность достигается за счет большого числа N (несколько десятков тысяч).

Угловая дисперсия, также как и в случае призмы, определяется угловым расстоянием между двумя спектральными линиями, отнесенными к разности длин волн. Дифференцируя (5) можно получить:

(7)