Раздаточный материал - 2014 логистика_1 / 02_03 - Основы теории и вероятности и мат_статистики / 02.1_3 - Cлучайная величина. Плотность и функция распределения. Числовые значения

4

2. Распределения случайных величин

2.1. Случайная величина

Численное представление исходов эксперимента именуется случайной величиной. Случайная величина - это функция (правило), отображающая пространство элементарных исходов на пространство действительных чисел.

Случайная величина – это функция (или правило), которая определяет вещественное число (от -¥ до +¥) каждому элементу в пространстве событий

Случайная величина х может быть дискретной или непрерывной. Например, случайная величина, связанная с бросанием игральной кости, является дискретной со значениями от 1 до 6, тогда как время между поступлениями заявок в систему обслуживания выражается непрерывной случайной величиной с положительными значениями.

Примеры: броски монеты (0,1), броски кубика – значение граней, интервал времени поступления клиентов в систему – положительное число, выпуск годных изделий (0,1), отклонение от допуска размера изделия (положительное и отрицательное действительное число) и т.д.

2.2. Плотность распределения и функция распределения случайной величины

Плотность распределения вероятностей (просто плотность вероятности) обозначается как f(x) (непрерывная случайная величина) или р(х) (дискретная случайная величина). Определяет значение вероятности, соответствующее значению x.

Функция распределения вероятностей F(x) случайной величины X:

F(x) = P(X <= x) для -¥ < x < +¥,

вероятность того, что в результате эксперимента случайная величина X получит значение, не превышающее x.

Свойства:

0 <= F(x) <= 1

неубывающая функция, т.е., если x1<x2, тогда F(x1) <=F(x2)

lim F(x) = 1 при x à ¥

Самой важной вероятностной характеристикой случайной величины является функция распределения, определяемая следующим образом (область определения от а до X)

- дискретная случайная величина

- непрерывная случайная величина

Функция распределения и плотность вероятности дискретной (слева) и непрерывной (справа) случайной величины

2.3. Числовые характеристики распределение дискретной случайной величины

Распределение дискретной случайной величины — это исчерпывающий список всех возможных значений случайной переменной, где каждому исходу поставлена в соответствие его вероятность. Например, на рисунке приведено распределение количества ипотечных займов, выданных в течение недели местным филиалом банка. Поскольку в таблице приведены все возможные исходы, сумма их вероятностей равна 1.

Рис. Распределение количества ипотечных займов, выданных за неделю

Математическим ожиданием μ дискретной случайной величины X называется среднее значение ее распределения. Эта величина равна сумме произведений всех значений случайной величины X на соответствующие вероятности Р(Х). Другими словами, математическое ожидание дискретной случайной величины X — это взвешенное среднее всех возможных исходов, где в качестве весов служат вероятности каждого исхода.

где X_i — i-e значение дискретной случайной величины X, Р(Х_i) — вероятность i-ro значения дискретной случайной величины X.

Стандартное отклонение σ (standard deviation) дискретной случайной величины:

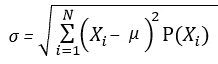
Дисперсия (variance) = σ2

Коэффициент вариаций = σ/ μ

Терминология

Математическое ожидание	Expected Value	μ
Стандартное отклонение	Standard Deviation	σ
Дисперсия	Variance	σ2
Коэффициент вариаций	Coefficient of Variation	v = σ/μ

Два важных замечания:

(1) Математическое ожидание

Допустим спрос и время поставки являются случайными величинами.

Если мы в качестве прогноза (спроса, времени поставки) мы выбираем математическое ожидание, то чему равна вероятность, что фактическое значение спроса (времени поставки) не превысит прогноз? 50%!

(2) Стандартное отклонение

Чем больше стандартное отклонение, тем большее число наблюдений необходимо для определения m с заданной точностью!

Большее значение стандартного отклонения при одном и том же значении математического ожидания свидетельствует о большем значении неопределенности случайной величины. Возрастает риск при использовании данной случайной величины в качестве прогноза!