Раздаточный материал - 2014 логистика_1 / 02_03 - Основы теории и вероятности и мат_статистики / 01.5 - Теорема Байеса

5

1.5. Теорема Байеса

Условная вероятность события учитывает информацию о том, что произошло некое другое событие. Этот подход можно использовать как для (a) уточнения вероятности с учетом вновь поступившей информации, так и для вычисления вероятности, что (b) наблюдаемый эффект является следствием некоей конкретной причины

Условные вероятности: P(A|B1), P(A|B2), P(A|B3) Теорема Байеса: Уточнить вероятность с учетом поступившей информации Решить обратную задачу относительно условной вероятности: произошло событие А, какова вероятность, что по причине B1? – P(B1/A)

Примеры задач, решаемых с помощью теоремы Байеса:

(1) Получено письмо-спам. Какова вероятность, что причина в наличии в нем определенного слова или словосочетания? (байесовский анти-спам фильтр):

(2) В партии смешаны готовые изделия от трех поставщиков. Взятое наугад изделие дефектно. Какова вероятность, что это изделие от поставщика 1?

(3) Имеется прибор, состоящий из 3-х узлов, каждый из которых имеет определенное время наработки на отказ. Произошел отказ прибора. Какова вероятность, что причина в узле 1?

(4) Медицинский тест дал положительный результат, какова вероятность, что человек действительно болен?

(5) Какова вероятность выиграть тендер на контракт, если заявку подаст конкурент-компания X?

(6) Какова вероятность хорошего спроса при благоприятном (неблагоприятном) прогнозе?

(7) Два стрелка независимо друг от друга стреляют по одной и той же мишени, делая каждый по одному выстрелу. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что эта пробоина принадлежит первому стрелку

Байесовская статистика

1. Вся традиционная статистика исходит из того, что наблюдатель ранее не располагал никакой информацией об объекте наблюдения.

2. В реальном мире данное допущение почти никогда не выполняется.

Проблема. Люди (практически все, даже математически подкованные) довольно плохо обращаются с вероятностями. Все мы преувеличиваем значение конкретного наблюдения, преуменьшая априорное знание (то есть, знание, имевшееся у нас до наблюдения).

Проблему прежних знаний изучает так называемая байесовская статистика. Автор этого метода — Томас Байес, британский математик и пресвитерианский священник XVIII века, самые известные работы по статистике которого были опубликованы только после его смерти.

Байесовская статистика изучает вопрос: Как мы корректируем свое предварительное знание с учетом новой информации?

• Байесовский анализ начинается с того, что (1) известно сейчас, и затем рассматривает, как (2) это знание изменится с получением новых сведений.

• Небайесовская (классическая) статистика, преподаваемая в большинстве ВУЗов, исходит из следующего: все, что известно о некоей группе объектов, — это выборка, которую вы только что из нее сделали.

Формула Байеса

P(B₁|A) = P(A|B₁) * P(B₁) / (P(B₁)*P(A|B₁) + P(B₂)*P(A|B₂) + … P(B_n)*P(A|B_n))

где B₁, B₂, … B_n — взаимоисключающие и исчерпывающие события.

Формула Байеса получается из формулы условной вероятности:

поскольку P(A)= P(B₁)*P(A|B₁) + P(B₂)*P(A|B₂) + … P(B_n)*P(A|B_n), то

P(B₁|A) = P(A|B₁) * P(B₁) / P(A))

В итоге получаем формулу условной вероятности:

P(A|B₁) = P(B₁|A) * P(A) / P(B₁) , где

P(A) – безусловная вероятность события A

P(B₁) – безусловная вероятность события B

P(A|B₁) – условная вероятность события A при событии B₁

P(B₁|A) – условная вероятность события B₁ при событии А

Пример 1 применения теоремы Байеса

Вероятность того, что человек страдает от определенного заболевания, равна 0,03. Медицинский тест позволяет проверить, так ли это.

Если человек действительно болен, вероятность точного диагноза (утверждающего, что человек болен, когда он действительно болен) равна 0,9.

Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02.

Допустим, что медицинский тест дал положительный результат.

Какова вероятность того, что человек действительно болен? Какова вероятность точного диагноза?

Введем следующие обозначения:

событие D — человек болен, событие D' — человек здоров, событие Т — диагноз положительный, событие Т' — диагноз отрицательный.

Из условия задачи следует, что Р(D) = 0,03, P(D') = 0,97, Р(T|D) = 0,90, P(T|D') = 0,02.

Тогда

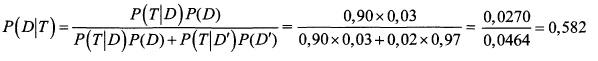
Вероятность, что при положительном диагнозе человек действительно болен, равна 0,582. Знаменатель формулы Байеса равен вероятности положительного диагноза = 0,0464

Пример 2 применения теоремы Байеса

Предположим, что компания, упомянутая выше, исследует рынок сбыта новой модели телевизора. В прошлом 40% телевизоров, созданных компанией, пользовались успехом, а 60% моделей признания не получили. Прежде чем объявить о выпуске новой модели, специалисты по маркетингу тщательно исследуют рынок и фиксируют спрос. Они выяснили, что в прошлом успех 80% моделей, получивших признание, прогнозировался заранее, в то же время 30% благоприятных прогнозов оказались неверными. Для новой модели отдел маркетинга дал благоприятный прогноз.

Какова вероятность того, что новая модель телевизора будет пользоваться спросом?

Введем следующие обозначения: событие S — телевизор пользуется спросом, событие S' — телевизор не пользуется спросом, событие F — благоприятный прогноз, событие F' — неблагоприятный прогноз. Допустим, что P(S) = 0,4, P(S') = 0,6, P(F|S) = 0,8, P(F|S') = 0,3. Применяя теорему Байеса, получаем:

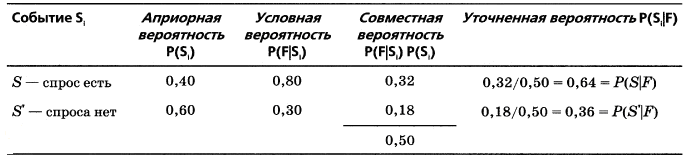
Вероятность спроса на новую модель телевизора при условии благоприятного прогноза равна 0,64. Таким образом, вероятность отсутствия спроса при условии благоприятного прогноза равна 1–0,64=0,36.

Литература по Байесовской вероятности

1. Лучше начать с относительно большого, но более-менее понятного и доступного Интуитивного объяснения теоремы Байеса.

2. Очень много различных применений Байеса описывает нобелевский лауреат по экономике Канеман (со товарищи) в замечательной книге Принятие решений в неопределенности: Правила и предубеждения.. Минимум формул.

3. Глава 6. Ложная положительность и положительная ложность из книги Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью. Ни одной формулы. Кстати, примеры на тему Байесовской вероятности встречаются не только в упомянутой главе.

4. Глава 10. Кое-что о Байесе, статистике и подходах из книги Дуглас Хаббард. Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе.

5. Раздел Условная вероятность. Теорема Байеса из книги Левин. Статистика для менеджеров с использованием Microsoft Excel.

6. Раздел Теорема гипотез (формула Байеса) из книги Вентцель, Овчаров. Теория вероятностей и ее инженерные приложения. Кратко и по делу. Формулы и несколько примеров с решениями.

7. Глава 5. Наше восприятие мира — это фантазия, совпадающая с реальностью из книги Криса Фрита. Мозг и душа.

8. Байесовский вывод. Коротенькая заметка в Викинауке – свободной научной энциклопедии на русском языке.

8. (издана еще в СССР): Дж. Хей. Введение в методы байесовского статистического вывода. В электронном виде можно найти в Интернете.