2.3.4. Методы построения функций принадлежности

Существуют прямые и косвенныеметоды построения функций принадлежности.

Прямые методыопределяются тем, что эксперт непосредственно задает правила определения функции принадлежности, характеризующей понятие. Это значение согласуется с его предпочтениями на множествеследующим образом:

1. Для ,тогда и только тогда, когдапредпочтительнее, т. е. в большей степени характеризуется понятием;

2. Для 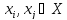,тогда и только тогда, когда ибезразличны относительно понятия.

К прямым методам отнесем методы, основанные на вероятностной трактовке функции принадлежности , т. е. вероятность того, что объектбудет отнесен к множеству, которое характеризует понятие.

В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям, экспертная информация является только исходной для дальнейшей обработки.

Рассмотрим пример косвенного метода построения функции принадлежности. Допустим, что nвидов действий или объектов рассматриваются группой экспертов. Цели экспертов:

1. Высказать суждения об относительной важности объектов;

2. Гарантировать такой процесс получения суждений, который позволит количественно оценить суждения по всем объектам (получить множество численных весов, сопоставленных отдельным объектам).

Пусть x₁,x₂,…,x_n— совокупность объектов (возможных действий). Количественные суждения о парах объектов (x_i, x_j) представляются матрицей размераnn.

Элементы определены следующим образом. Если, то,. Еслиx_ix_j, т. е. имеют одинаковую значимость, то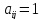,(по шкале Саати, таблица 2.3).

В частности для всехi. Тогда матрица парных сравнений имеет вид (2.46). Задача ставится следующим образом, по суждениям,nвозможных действийx₁,x₂,…,x_n, поставить в соответствие значения функции принадлежности (как весов объектов)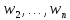.,, и матрица парных суждений имеет вид (2.47).

Соответственно: ,,.

Таблица 2.3

Качественные оценки градации альтернатив

Оценка важности	Качественная оценка	Примечание
1	Одинаковая значимость.	Альтернативы имеют одинаковый ранг.
3	Слабое превосходство.	Соображения превосходства одной альтернативы над другой малоубедительны.
5	Сильное превосходсво.	Имеются надежные доказательства существенного превосходства одной альтернативы.
7	Очевидное превосходство.	Существуют убедительные свидетельства в пользу одной альтернативы.
9	Абсолютное превосходство.	Свидетельство в пользу предпочтения одной альтернативы перед другиой в высшей степени убедительно.
2, 4, 6, 8	Промежуточные значения	Используется, когда необходим компромисс.

Потребуем, чтобы для всех элементов множества выполнялось равенство:

Степени принадлежности элементов множеству будем определять посредством парных сравнений. При этом используются оценки, приведенные в таблице 2.3 (шкала Саати).

Оценку элемента по сравнению с элементом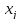с точки зрения свойства обозначим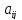. Для обеспечения согласованности примем. Оценкисоставляют матрицу.

Найдем — собственный вектор матрицы, решая уравнение, где— собственное значение матрицы. Вычисленные значения, составляющие собственный вектор, принимаются в качестве степени принадлежности элементовxмножеству.

(2.49)

Всегда выполняется равенство , найденные значения тем точнее, чем ближекn. Отклонениеотnможет служить мерой согласованности суждений экспертов.

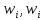Суждения экспертов позволяют оценить парные сравнения объектов, т. е. ,. Возьмем любую строку значений матрицы парных сравнений:. Умножим:, получим строку:,…,изn значений, которые будут различаться, тогда целесообразно вычислить среднее.

При согласованных суждениях экспертов процедура построения функций принадлежности упрощается. Согласованная матрица парных сравнений обладает следующими свойствами:

1. Матрицу A будем называть положительной, если>0,.

2. Матрицу A будем называть обратносимметричной, если,.

3. Матрицу Aбудем называть согласованной, если.

4. Положительная обратно симметричная матрица согласована тогда и только тогда, когда .

5. Диагональные элементы матрицы = 1,.

Свойства 1, 2, 3, 4 позволяют определить все элементы матрицы парных сравнений, если известны (n–1) недиагональных элементов. Например, если известнаk-я строка‚ т. е. элементы, то произвольный элементопределяется как:

6. Положительная матрица Aсогласована в том и только в том случае, если она единичного ранга и элементы ее главной диагонали равны единице.

Ранг матрицыAесть порядок наибольшего квадратного массива (подматрицы), детерминант которого не равен нулю.

Матрица, каждая строка которой может быть получена умножением одной строки на некоторую постоянную — вырожденная (det(A) = 0) и имеет единичный ранг. Если положительная матрицаAсогласована, то каждая строка является положительным кратным любой заданной строки. Т. е. положительная согласованная матрица при= 1,имеет общий вид:

Под согласованностью будем понимать, что при наличии некоторого базового массива данных, остальные данные могут быть логически получены из них.