Калибровочные соотношения между альтернативами

Наименование.	Соотношение между элементами.
Простая структура.	Диагональные элементы при этом не фиксируются и могут быть любыми.
Турнирная калибровка.	Для всех и, для которых:.
Степенная калибровка.	Для всех и, для которых:.
Кососимметричная калибровка.	Для всех i и j: .
Вероятностная калибровка.	Для всех и:;.

Вероятностная калибровка — , характеризует вероятность превосходстванад.

Рассмотренные калибровочные соотношения могут быть отражены на графовых моделях. Рассмотрим постановки задач принятия решений в различных средах.

2.1. Однокритериальные задачи в условиях определенности

Простейшая, однокритериальная задача выбора возникает, когда принятие конкретного решения xприводит к однозначному исходуy, оцениваемому с помощью единственного критерия. Предполагается однозначная зависимость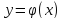. «Полезность» исходов можно определитьфункционалом:, где , дляx, соответствует числовая оценка.

Функционал Fпозволяет в явном виде отразить систему предпочтений ЛПР. Будем считать, чем больше значениеF, тем более предпочтительна данная альтернатива.

Обозначим суперпозицию функций fи черезF, приходим к оптимизационной задаче:

Функционал F(x) будем называтьцелевым функционаломилицелевой функцией. Требуется построить множество:

Например, бинарное отношение может быть задано следующим образом:тогда и только тогда, когда.Если, то точки, несравнимы поRи. Такое отношение обладает антирефлексивностью, асимметричностью, транзитивностью и поэтому является отношением строгого порядка на X.

Функционал F(x) может порождать различные системы предпочтений, выраженные на языке бинарных отношений, а задача построений ядра оказывается эквивалентной задаче скалярной оптимизации (2.1). Терминскалярныйозначает, что значения функционалаF(x) — элементы множества действительных чиселE—cкаляры. Если существует функционалF(x), то задача ПРсводится к задаче оптимизации (2.1). Не всякое бинарное отношениедопускает описание с помощью целевой функции, т. к. отношение должно быть транзитивно и линейно, что не всегда. Следовательно, язык бинарных отношений существенно более общий для описания системы предпочтений, чем язык целевых функций.

2.2. Многокритериальные задачи в условиях определенности

В случае многокритериальной задачи, любому решению соответствует единственный элемент,, но в данном случае «качество» или «полезность» исходаyоценивается несколькими числами(), причем каждый из функционалов требуется максимизировать. С помощью суперпозиции, (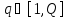) можно непосредственно оценивать качество самого решенияx, используя векторное отображение.

Пусть . Если,(), причем, по крайней мере, одно из неравенств — строгое, то будем говорить, чтопредпочтительнее. Если для некоторогоне существует более предпочтительных точек, то будем называтьэффективнымилиПарето-оптимальнымрешением многокритериальной задачи:

Множество, включающее в себя все эффективные (максимальные) решения, обозначим 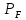(X) илиP(X) (для известного векторного отображения) будем называтьмножеством Паретодля векторного отображенияF:Y, , (X)  X.

Множество P(F) = F(P(X)) будем называть множествомэффективных оценок.

Согласно принципу Паретооптимальное решение необходимо искать среди элементов множестваP(X). В противном случае всегда найдется точка, оказывающаяся более предпочтительной с учетом всех частных целевых функций.

Точку 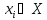будем называтьслабо эффективнымрешением задачи (2.3), если не существует, для которой выполняются строгие неравенства, (). Т. е. решение называется слабо эффективным, если оно не может быть улучшено сразу по всем критериям «полезности», задаваемых с помощью, (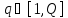). Множество слабо эффективных решений обозначимилиS(X),S(F) =F(S(X)).

Системы предпочтений на множестве альтернатив , заданные с помощью векторного отображенияFмогут быть представлены на языке бинарных отношений,:

, . (2.4)

, . (2.5)

Бинарное отношение — называют отношением строгого доминирования илиотношением Слейтера, а—отношением Парето. Ядра этих отношений совпадают с множествами,.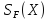

Цель многокритериальной задачи оптимизации, исходя из формальной модели общей задачи ПР,состоит в выделении множества эффективных (слабо эффективных)элементов изX. Отношения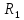,в общем случае не являются линейными, т. е. существуют несравнимые по, элементы множестваX.

Формирование соответствующих бинарных отношений осуществляется ЛПР на основе своих предпочтений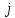.