Назначение c1o3 по критериям

C1	3	3	1	1	2
O3	3	3	1	1	2

Векторы: С₁₃= (0 0 0 0 0),O₁₃= (0 0 0 0 0).

Таблица 6.4

Назначение C₄O₁ по критериям

C4	2	3	2	1	1
O1	2	3	2	1	2

Векторы: C₄₁= (0 0 0 0 1),О₄₁= (0 0 0 0 0).

Таблица 6.5

Назначение C₂O₂ по критериям

C2	2	2	3	1	2
O2	2	2	3	2	1

Векторы: С₂₂= (0 0 0 1 0), О₂₂= (0 0 0 0 1).

Таблица 6.6

Назначение C₃O₄ по критериям

C3	1	1	2	2	3
O4	1	1	3	2	2

Векторы: C₃₄= (0 0 1 0 0),О₃₄= (0 0 0 0 1).

Теперь возможен анализ назначений и учет предпочтений ЛПР.

6.3. ЗАДАЧА ПЛАНИРОВАНИЯ ПРОИЗВОДСТВА

Пусть некоторое предприятие производит Nтипов продукции, затрачивая при этомMресурсов. Известно:— количествоi-го ресурса, необходимое для производства единичного количестваj-й продукции (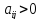),) ,). Обозначим:— запасi-го ресурса на предприятии;— цена единичного количестваj-й продукции.

Предполагается, что затраты ресурсов растут прямо пропорционально объему производства.

Пусть — планируемый объем производстваj-й продукции. Допустимым является такой набор производимой продукцииx= (x₁,x₂, …,x_n), при котором суммарные затраты каждого видаi-го ресурса не превосходят его запаса (6.11).

Стоимость набора продукции x:.

Задача: при всех наборах векторов x, удовлетворяющих ограничениям найти такой, при котором:

Пример. Пусть некоторое предприятие производит три вида продукции: x₁, x₂,x₃ (таблица 6.3).

Таблица 6.3

Затраты на производство единицы продукции

	Прод.	1	2	3
Ресурс
1		1	4		4
2		2	1		4
3		4	2		4

На производство затрачивается три вида ресурсов. Запасы ресурсов на складе (таблица 6.4). Цена каждого из видов продукции (таблица 6.5).

Таблица 6.4

Запасы ресурсов

Ресурс	Кол-во
1	120
2	60
3	100

Требуется решить задачу условной максимизации функционала (дохода предприятия):

(6.13)

Таблица 6.5

Цена единицы продукции

Продукция	Цена
1	30
2	22
3	56

при ограничениях:

(6.14)

Например, задача решается симплексным методом.

6.4. Задача Принятия решений в условиях риска

Пусть существует функция y=A(x,f), гдеxX— множество альтернатив (решений),fF— множество состояний среды,yY— множество исходов. Особенностью рассматриваемых задач таких задач ПР является предположение о неизвестном в момент принятия решения значении параметраF. ФункциюAбудем называть функцией реализации. Такая функция ставит в соответствие каждой паре (x,f) исходy. Будем предполагать, что каждой альтернативе соответствует распределение вероятностей на множестве исходов. Тогда связи альтернатив с исходами, можно отобразить в виде графа (рис. 6.24).

Точка ЛПР соединяется стрелками с альтернативами x_i, которые доступны ЛПР. Рядом со стрелками могут быть указаны веса — вероятности наступления соответствующего исхода (сумма весов, выходящих из одной вершины должна быть равна единице).

Рис.6.24. Граф связей альтернатив с исходами

Пусть существуют Nальтернатив иKисходов. В качестве «состояний внешней среды» возьмем множество возможных связей альтернатив с исходами:f_j:XY,В случае конечных множествXиY:, где— количество стрелок, исходящих из альтернативыx_iна графе связей альтернатив и исходов. Каждое состояние средыf_jсоответствует подграфу (будем называть его подграфом состояния), в котором из каждой альтернативыx_iисходит только одна стрелка, указывающая какой исход будет реализован при выборе альтернативыx_i(S— максимально возможное число таких подграфов).

Выбор «состояния среды» f_jи альтернативыx_iполностью определяет исходy_j(x_i). Каждому состоянию внешней среды соответствует вероятность его наступления (вероятность реализации соответствующего подграфа состояния):

где 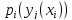— заданная вероятность наступления исходаy_jпри выборе альтернативыx_i.

Задача ПР в условиях риска в форме функции реализации означает, что статистическую неопределенность, проявляющуюся в неоднозначной (вероятностной) связи между альтернативой и результатом, можно всегда интерпретировать как существование некоторой среды, оказывающей влияние на результат.

На последней минуте хоккейного матча, при ничейном счете, тренер команды должен принять решение о замене вратаря шестым полевым игроком. Статистика, имеющаяся у тренера, показывает, что в аналогичных условиях в предыдущих встречах замена вратаря в 1/6 части случаев привела к выигрышу, в половине случаев — к ничьей и в одной трети случаев — к поражению. Если вратарь не менялся, то в 7/8 случаев встреча заканчивалась вничью, а в 1/8 части случаев команда проигрывала.

Построим граф связей альтернатив и исходов (рис. 6.25).

Рис. 6.25. Граф связей

Альтернативы: х₁— заменить вратаря,х₂— не делать замены. Исходы: выигрыш —, В, поражение —, П, ничья —, Н.

Задание функции реализации означает, что при известном

мы по каждому ходнозначно определяем исходy. Знаямы должны точно знать исход при выборе альтернативыx_i.

Выберем следующие шесть «состояний среды»:

f₁:x₁→ В,х₂→ Н;p(f₁) = 1/67/8 = 7/48,

f₂:x₁→ Н,х₂→ Н;p(f₂) = 1/27/8 = 7/16,

f₃:x₁→ П,х₂→ Н;p(f₃) = 1/37/8 = 7/24,

f₄:x₁→ В,х₂→ П;p(f₄) = 1/61/8 = 1/48,

f₅:x₁→ Н,х₂→ П;p(f₅) = 1/21/8 = 1/16,

f₆:x₁→ П,х₂→ П;p(f₆) = 1/31/8 = 1/24.

Функция реализации может быть представлена (рис. 6.26).

	F
X
х1		В	Н	П	В	Н	П
х2		Н	Н	Н	П	П	П

	F
X
х1		2	1		0		2		1		0
х2		1	1		1		0		0		0

Рис. 6.26. Табличное задание функции

Среднее:

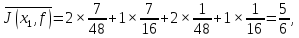
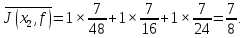
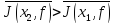не заменять вратаря в среднем приводит к успеху.

Замена задачи 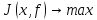задачейне единственный способ перейти к статистической постановке задачи.

Например, с учетом дисперсии критериальной функции J.

(6.16)

где — дисперсия случайной величины;k— заданная постоянная. Эту постоянную целесообразно интерпретировать как степень несклонности к риску.— определяет «степень важности» дисперсии по отношению к математическому ожиданию случайной величины.

Увеличение kприводит к уменьшению «среднего дохода», но уменьшается и вероятность отклонения от «среднего дохода» (в том числе в сторону уменьшения). Таким образом, чем выше k, тем менее склонно лицо к риску.