5.1. Уравнение эйлера

Определим линейный функционал, L(y(x)), как линейную функцию в линейном пространстве со следующими свойствами.

1. L(y(x) + y₁(x)) = L(y(x)) + L(y₁(x))

2. L(y(x)) есть непрерывный функционал.

Например L(y) =dx,L(y) =dx, где— произвольная функция от x.

Для экстремума дифференцируемых функций, определенных на линейных метрических пространствах, в точке экстремума первый дифференциал обращается в нуль. В применении к функционалам можно положить, что необходимое условие экстремума функционала — обращение в нуль его первого дифференциала.

Пусть есть функционал. Дифференциал функционала, заданного в некотором функциональном пространстве (при переходе от функцииy(x) к новой функцииy₁(x) должен быть линейным функционаломL(y₁ –y), такой, чтоL(y₁) –L(y) –L(y₁–y) есть величина, стремящаяся к нулю быстрее расстоянияr(y,y₁), т. е.I(y₁) =I(y)L(y₁–y) r(y,y₁), гдестремится к нулю быстрее расстоянияr(y,y₁). Обозначим первый дифференциал функционалаI(y) его вариациейI:

I=L(y₁ –y) (5.1)

Исследуем на экстремум функционал:

где ,— дважды дифференцирумая функция своих аргументов, т. е. Fобладает непрерывными частными производными до второго порядка включительно по всем аргументам.y =y(t) — кривая, на которой функционалIпринимает определенное значение. Будем полагать, чтоy =y(t) обладает первой и второй непрерывными производными. Полагаем, что для всех линий, достаточно близких к линииy =y(t), функционалIтакже определен. Построим кривуюy=y₁(x) =y(x)+y(x), близкую к кривойy=y(x). Пустьy₁(x) совпадает сy(x) для всех значенийx, лежащих вне малого интервала [x₁,x₂], содержащего некоторую избранную абциссуc(x₁<c<x₂). При построении кривыеy(x) иy₁(x) определяют некоторый бугорок, возвышающийся над кривойy(x). Площадь такого бугорка равна:

Функциональной производной в точкеcбудем называть предел отношения приращения функционалаI(y₁) –I(y) к площади, когда бугорок стягивается в точку.

Рассмотрим y(x) на функциональном пространстве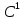всех дифференцируемых функций, обладающих непрерывной производной, причем за расстоянияr(y,y₁) между функциямиy(x) иy₁(x) примем их близость первого порядка:y=y(x) = y₁(x) –y(x),yобладает непрерывной производной:

Запишем вариацию функционала:

Из преобразования для вариации функционала:

и из требования, чтобы Iобращалось в нуль для произвольной функцииy, Лагранж вывел уравнение Эйлера:

Этому уравнению должна удовлетворять функция y=y(x), дающая экстремум интегралу:

Кривые удовлетворяющие уравнению Эйлера называют экстремалями.

5.2. Формализация задаЧи синтеза оптимальНого управления

Пусть движение объекта автоматического регулирования описывается, в общем случае нелинейным дифференциальным уравнением n-го порядка.

(5.9)

где ;;kn;u=u(t)—сигнал управления;x=x(t)—выходная (регулируемая) величина;—возмущение;,—производные регулируемой величины и возмущения;——нелинейные функции,t—время. Рассматриваются нелинейные аналитические функции, которые однозначно определены при всех абсолютных значениях аргумента в интервале [0,].

Задача синтеза оптимального управления автоматическими системами: найти такой закон управления объектомОв виде функции регулируемой величины, задания и возмущения:

(5.10)

где — задающее воздействие,r — порядок производной задания; чтобы мини-мизировать или максимизировать интегральный критерий:

где F — заданная функция;r — порядок производной задания;T — рассматриваемый промежуток времени.

б

а

Рис. 4.1. Объект (а) и структура оптимального управления (б): У—управляющее устройство;О—объект регулирования

Задача поставлена как детерминированная, т. е. поведение системы в будущем целиком и полностью определяется ее состоянием в данный момент времени и величиной управления.

Построение оптимальных систем связано с решением родственных математических задач, которые делятся на два класса.

1. К первому относятся задачи, связанные с определением и расчетом самого режима невозмущенного воздействия. Ищется алгоритм автоматического управления, при котором данное невозмущаемое движение приобретает требуемые экстремальные свойства. Такие системы будем называть оптимальными по режиму управления.

2. В другом классе задач ищется регулятор, гарантирующий существование заданных свойств возмущенного движения (переходного процесса). Такие системы будем называть оптимальными по переходному процессу.

В обоих случаях задача оптимизации может быть трактована как двухточечная граничная задача, к решению которой применимы все методы вариационного исчисления.

В первом случае решение задачи получается в виде известных функций времени u = u(t). Это решение не очень удачно, ибо такое управление существенно зависит от начальных условий движения и не может скомпенсировать неизбежные изменения параметров объекта, так как является разомкнутым.

Во втором случае ищется закон регулирования в его аналитической форме, как некоторая функция исходных координат системы, т. е. задача состоит в конструировании дифференциального уравнения регулятора.

Помимо отыскания оптимального управления только как функции координат системы или только функции времени, в некоторых случаях целесообразно определять оптимальное управление в функции координат системы и времени: .

Одной из сложных задач, возникающих при синтезе оптимального управления, является учет ограничений величины управляющего воздействия (насыщение):

(5.12)

и скорости его изменения:

(5.13)

Ограничения (5.12) и (5.13) могут выполняться в отдельности и в определенных комбинациях.