Устойчивые и неустойчивые решения.

2 1	Б	Р
Б	(1,1)	(0,3)
Р	(3,0)	(-9,-9)

Ситуации (Б,Б) и (Р,Р) являются неустойчивыми, т. к. каждый из водителей может получить лучший результат за счет одностороннего изменения своего решения. Например, водитель 1 в ситуации (Б,Б) может получить лучший результат, изменив стратегию на Р. Он получит выигрыш 3 вместо 1. Аналогично и для игрока 2. Это справедливо и для ситуации (Р,Р).

Ситуации (Б,Р) и (Р,Б) являются устойчивыми, поскольку если они возникли, ни у одного из игроков нет основания для одностороннего изменения стратегии поведения.

4. Методы многокритериальной оптимизации

Рассматривается задача X— множество сравниваемых альтернатив (объектов),R— бинарное отношение на множествеX. Пусть задано множество, состоящее изQкритериев, имеющих шкалы оценки альтернатив;n— номер оценки по шкалеq-го критерия— множество оценокq-го критерия, расположенных в порядке возрастания их качества (шкалаq-го критерия):. — множество векторных оценок; качество каждого объектаоценивается вектором ,,.

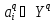Каждому критерию ставится в соответствие число w_q, (удельный вес) характеризующее важность критерия. Веса критериев определяются с помощью ЛПР или экспертов.

Системы предпочтений на множестве альтернатив , заданные с помощью векторного отображенияF:Y→E^Qможет быть представлены на языке бинарных отношений,, либо отношением Слейтера, либо отношением Парето:

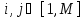, , (4.1)

, , (4.2)

где — отношение Слейтера,— отношение Парето.

Цель многокритериальной задачи оптимизации— построение ядра (подмножества максимальных, доминируемых элементов):

Максимальные элементы образуют между собой отношение несравнимости , т. е. могут существовать симметричные (эквивалентные) элементы, на которых существует отношение транзитивности.

4.1. Аксиоматическая теория полезности

Целью многокритериальной теории полезности отразить предпочтения ЛПР в числовом виде при выборе из некоторого множества элементов. Выбор вариантов в условиях определенности на основе теории полезности состоит в построении некоторого функционала U(x), определенного на множестве оценок альтернатив. Такой функционал позволяет формально свести многокритериальную задачу к однокритериальной. Будем называть функционалU(x)функцией полезности.

Предполагается, что функция полезности имеет аксиоматическое обоснование. Перечислим такие аксиомы.

1. Аксиома связности, когда для ,илиили.

2. Аксиома транзитивности, когда для таких, чтои.

3. Для соотношений между полезностями альтернатив , имеющими вид:

где U(x) — функция полезности альтернативы, можно найти такие числа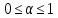,, что:

4. Аксиома рефлексивности: для которыхи.

5. Аксиома эквивалентности: , тогда на подмножестве эквивалентных элементов отношение симметрично.

Аксиома 3 предполагает, что функция полезности непрерывна и можно использовать любые малые части полезностей.

Для построения функции полезности предполагаются условия независимости альтернатив:

1. По разности. Предпочтения между двумя альтернативами, отличающиеся только оценками по порядковой шкале одного критерия ,не зависят от фиксированных значений оценок по другим критериям.

2. По полезности. Критерий будем называть независимым по полезности от критериев, если порядок предпочтения лотерей, в которых меняются только уровни критерия, не зависят от фиксированных значений оценок по другим критериям.

3. По предпочтению. Два критерия независимы по предпочтению от других критериев, если предпочтения между альтернативами, различающиеся только значениями оценок по, не зависят от фиксированных значений оценок по другим критериям.

Если на множестве альтернатив выполняются условия независимости по полезности и предпочтению, то функция полезности является аддитивной:

либо мультипликативной:

где ,— функции полезности, изменяющиеся от 0 до 1;— веса критериев,; коэффициентk> – 1.

Таким образом, многокритериальную функцию полезности можно определить, если известны значения коэффициентов , а также однокритериальные функции полезности.

Если отказаться от аксиомы связности и оставить понятие несравнимых по Парето альтернатив, то имеем основную задачу многокритериальной оптимизации — построение множества Парето. Построение функции полезности возможно только на основе диалога с ЛПР.