3.6. Основные понятия теории игр
Постановка задачи принятия решений следующая:
В
задаче полагается, что фактором
неопределенности
управляет «разумный» противник. Его
цели выражаются аналогично (3.31):
Такая задача (неопределенность типа «активный партнер») относится к теории игр. Противоборствующие стороны будем называтьигроками; выбираемые противниками альтернативы (xиz)—ходами; правила выбора решений—стратегиями; значения функционаловJиI—выигрышами.
Расхождение между функционалами JиIопределяет степень антагонизма игроков. Может оказаться, чтоJ= –Iпри любыхxиz. Такую игру будем называть антагонистической, строго конкурентной, игрой с нулевой суммой (J+I= 0). Такая антагонистическая ситуация является вырожденной. Более типичен конфликт, в котором интересы игроков не совпадают, но и не строго противоположны.
Представим
ситуацию, когда не два, а kигроков максимизируют свои выигрыши
(
,
,…,
),i=1,…,k.
Пусть
для первого игрока, выбирающего решение
,
остальные составляют фактор неопределенностиz:pi(x1,
z)
.
Если
=0,
то мы говорим об игре с нулевой суммой.
Будем рассматривать игры двух лиц А —
(3.31) и Б — (3.32). В общем случае,X
,Z
— векторные пространства разных
размерностей. Представим задачу в виде
таблицы (рис.3.2).
|
|
|
|
|
|
Рис. 3.2. Постановка задачи игры для двух игроков.
На
пересечении строки iи столбцаjстоит пара
чисел (p,q),
гдеp=J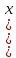
),q=I
),
с точки зрения игрока А. Функционалы
требуется либо максимизировать, либо
минимизировать, в зависимости от
постановки задачи. В дальнейшем
рассматриваем задачи с позиции игрока
А. При принятии решений в условиях риска
(подобные задачи могут быть отнесены к
теории игр), предполагалось, что сторона
Б — это внешние факторы («природа»).
При игре с «думающим» противником введем
гипотезы суть которых выделяет в теории
ПР отдельную теорию — теорию игр. Будем
различать следующие основные гипотезы.
1. Пусть каждый из субъектов А и Б не имеет информации о выборе противоположной стороны. Будем поступать аналогично задаче принятия решений в условиях полной неопределенности.
Для субъекта А:
Для субъекта Б:
Решая задачи максимизации (3.33), (3.34) находим соответствующие векторы x* и z*.
Рассмотрим
пример.
,
.
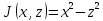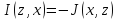Имеем антагонистическую игру:
,
;
,
.
Считаем,X
= Z
= R,
есть множество вещественных чисел.
.
Обозначим:
(3.35)
По
постановке задачи (3.35) любой
уменьшаетJ.
Тогда запишем:
.
,
достигается
при x
= 0.
Гарантированный результат
,
при
.
Это гарантированный результат. При
любомz
имеем значение J
не хуже (не больше) чем ноль:
.
На
рис. 3.3 приведены линии постоянного
уровня функционала
на плоскости
.
Рис.
3.3. Линии постоянного уровня (
)
Линией
уровнябудем называть геометрическое
место точек на плоскости, где
.
Если функция зависит более чем от двух
переменных, то говорят оповерхностях
уровня.
При
выборе гарантирующего решения
,
при различных z обеспечивается
.
2.
Предполагаем, что субъект Б следует
принципу максмина и выбирает
из условия (3.34). Тогда можно выбратьx
из условия:
где z* — гарантирующее решение игрока Б. Обозначим решение задачи (3.36) через x**. Оказывается что
где
— гарантированная оценка субъекта А,
получаемая по принципу максмина (3.36).
Неравенство (3.37) может быть строгим,
тогда, следуя гипотезе 2 можно получить
выигрыш, выбираяx**,
а не x*.
Рассмотрим пример, игру с нулевой суммой (таблица 3.3).
На пересечении строки и столбца стоит значение критерия (выигрыш игрока А, или проигрыш игрока Б).
Минимаксная
гарантирующая стратегия игрока А — x*=
x3,
гарантированная оценка
.
Если бы игрок А выбрал другое
Таблица 3.3