Слои Парето.
Поскольку вероятность того, что исходное множество будет одновременно являться и множеством Парето (состоять из несравнимых объектов) крайне мала, то будем выделять т.н. слои Парето. Один слой формируется следующим образом:
- из исходного множества выделяется недоминируемый элемент
- затем выделяются все несравнимые с ним объекты
Выделенные объекты заносятся в новое множество, называемое слоем Парето. Затем исходное множество, из которого теперь удалены «лучшие» объекты, обрабатывается по тому же принципу до тех пор, пока обработке и занесению в свой слой не подвергнется каждый его элемент. Каждый слой Парето является элементом множества подмножеств исходного множества. На рис. 4.1 показан граф, иллюстрирующий пример отношения доминирования на множестве. Исходящая стрелка обозначает доминирование объекта, из которого она исходит, над объектом, на который она указывает. Двунаправленная стрелка говорит о том, что объекты несравнимы (4 14, 8 13). Узел 5 является доминирующим на исходном множестве, поэтому на рисунке он не имеет ни одной входящей стрелки, в т.ч. двунаправленной, а только исходящие. Поэтому его можно выделить во множество (слой) Парето, которое будет состоять только из одного элемента. На рисунках 4.2 – 4.8 показан процесс изменения исходного множества по мере выделения из него слоёв Парето.
Рис. 4.1. В центре расположен недоминируемый объект (узел графа).
Рис. 4.2.
Рис. 4.3.
Рис. 4.4.
Рис. 4.5.
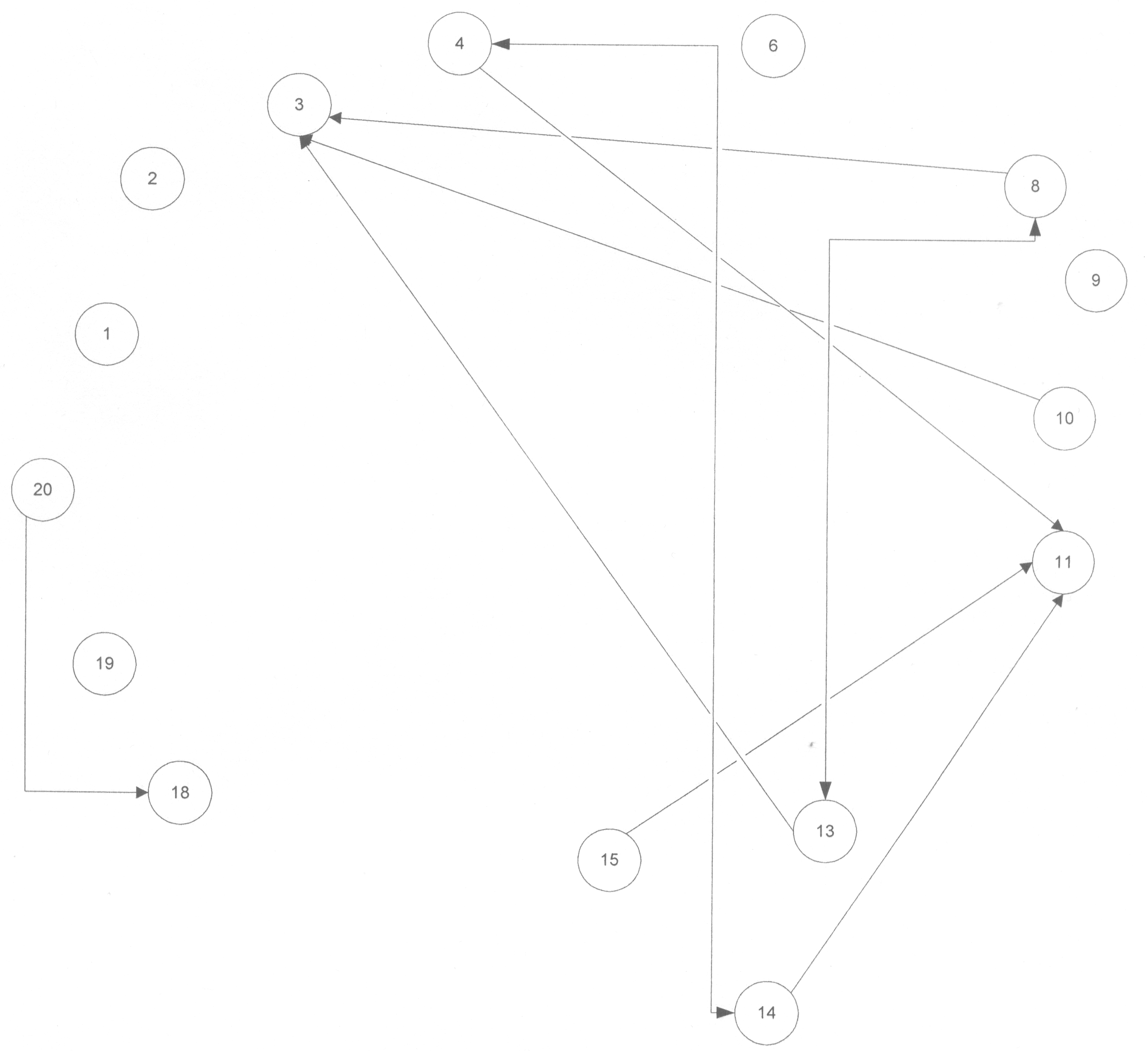
Рис. 4.6.
Рис. 4.7. Рис. 4.8
В результате осуществелённых операций объекты исходного множества распределились по слоям Парето следующим образом:
[5]
[7]
[17]
[16]
[12]
[4][8][13][14]
[10][15][20]
[1][2][3][6][9][11][18][19]
Сравнение упаковки объектов для сортировки по полезности и для распределения по слоям Парето.
В таблице 4.1 представлены объекты, отсортироавнные по полезности:
Таблица 4.1. Сортировка по полезности.
|
№ объекта |
Значение функции полезности |
|
5 |
15 |
|
7 |
14 |
|
8 |
12 |
|
13 |
12 |
|
16 |
12 |
|
4 |
11 |
|
9 |
11 |
|
12 |
11 |
|
14 |
11 |
|
15 |
11 |
|
2 |
10 |
|
19 |
10 |
|
20 |
10 |
|
6 |
9 |
|
10 |
9 |
|
18 |
9 |
|
1 |
8 |
|
3 |
8 |
|
11 |
8 |
Упакуем объекты в контейнеры, отсортировав их по полезности (Таб. 4.2)
Таблица 4.2. Распределение объектов по контейнерам после сортировки по полезности.
|
Номера контейнеров |
1 |
2 |
3 |
4 |
5 |
|
Номера объектов |
5, 7, 8 |
17, 16 |
13, 9, 12 |
4, 14 |
15, 2 |
Величина суммарной полезности: 144.
А теперь упакуем их после распределения по слоям Парето (Таб. 4.3)
Таблица 4.3. Распределение объектов по контейнерам после распределения по слоям Парето.
|
Номера контейнеров |
1 |
2 |
3 |
4 |
5 |
|
Номера объектов |
5, 7, 8 |
17, 16 |
13, 9, 12 |
4, 14 |
15, 2 |
Величина суммарной полезности: 120.
На рис. 4.9 представлен график, отображающий результаты упаковки для обоих слчаев распределения объектов.
Вывод.
Рис. 4.9. Представление результатов упаковки.
Вывод.
Была выполнена упаковка 20 объектов, каждый из которых имеет свои характеристики массы и объёма. Упаковка производилась в 5 контейнеров двумя способами: по полезности и по слоям Парето. В обоих случаях количество упакованных объектов одинаково. Оценка результатов упаковки для варианта по слоям Парето в данной задаче оказалась хуже, чем для упаковки по полезности.