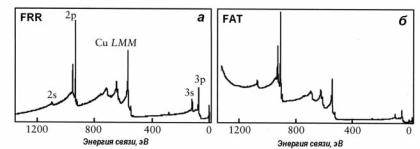
Рис. 2.8. Обзорный фотоэлектронный спектр Cu, измеренный в различных режимах работы полусферического анализатора: а – с постоянным коэффициентом замедления (режим FRR), б – с постоянной энергией пропускания (режим FAT) [17]
Влияние геометрии эксперимента
В общем случае угол между направлением движения фотоэлектронов, попадающих в энергоанализатор, и поверхностью образца может быть любым. В том случае, когда фотоэлектроны вылетают не по нормали к образцу, размер анализируемой области поверхности образца определяется не только площадью входной щели анализатора, но и углом α поворота образца относительно этой щели (см. рис.2.5), что также влияет на интенсивность фотоэлектронных пиков.
С учетом этого, аппаратный фактор можно представить в следующем виде:
C = I0 |
A0 |
T (KE) F(KE) , |
(2.17) |
|
sinα |
||||
|
|
|
где I0 – интенсивность падающего рентгеновского излучения; Т(КЕ) пропускающая способность анализатора, F(KE) – эффективность детектора фотоэлектронов, равная отношению числа электронов, зарегистрированных детектором, к общему числу попадающих на него электронов.
2.4.4.Интенсивность фотоэлектронной линии
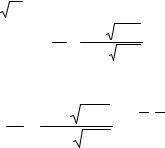
Вобщем виде интенсивность фотоэлектронного пика с учетом выражений (2.12), (2.14) и (2.17) может быть представлена как:
|
|
|
A |
|
σ |
nl |
|
|
1 |
3 |
|
|
− |
d |
|
||
|
|
|
|
|
|
|
|||||||||||
I = I |
0 |
|
0 |
T (KE) F(KE) k |
|
1 |
+ |
|
β |
|
sin 2 |
θ −1 |
|
c λ e λ . (2.18) |
|||
|
|
|
|
|
|||||||||||||
|
|
sinα |
|
4π |
|
|
2 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
47
Для проведения количественного анализа образца методом РФЭС, т.е. для определения атомных концентраций сi составляющих его элементов, рассматривают соотношение интенсивностей основных фотоэлектронных линий элементов, присутствующих в образце. Для примера рассмотрим двухкомпонентный образец, состоящий из атомов элементов 1 и 2. Тогда отношение интенсивностей их фотоэлектронных линий в режиме работы анализатора FAT c T~1/KE составляет:
|
|
|
c σ |
|
|
1 |
|
|
3 |
sin 2 |
|
λ k KE |
|
|
|
||||||||||||
|
|
|
1 |
+ |
|
β |
1 |
|
|
|
|
θ −1 |
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
I1 |
|
|
1 |
1 |
|
2 |
|
|
2 |
|
|
|
|
1 |
1 |
|
. |
(2.19) |
|||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
I |
2 |
c |
|
|
|
|
1 |
|
|
3 |
sin 2 |
|
|
|
k |
|
KE |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
σ |
1 |
+ |
|
β |
2 |
|
|
|
|
θ −1 |
|
λ |
2 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Здесь мы сократили все величины, остающиеся одинаковыми для данного спектра (I0, A0, α) и пренебрегли различием эффективности детектирования F(KE) и коэффициента k, учитывающего сателлиты. Оценим роль величины β, которая может быть различной ( −1≤ β ≤ 2 ) для оболочек рассматриваемых элементов. Наиболь-
шее возможное значение отношения I1 / I 2 достигается при β=2 и sin2θ = 1 и равно I1 / I 2 =1.5 . Наименьшее значение достигается при β=−1 и sin2θ = 1 и равно I1 / I 2 = 0.75 . Следовательно, максимальная ошибка в результате пренебрежения величиной β (т.е. считая β1 = β2 ) составит 50%. Однако на практике обычно она не
превосходит ~20%. Для простоты далее мы также пренебрежем различием в коэффициенте k = 0.8–0.9.
Тогда считая λ ~ E , получим простое соотношение: |
|
||||
I1 |
c1σ1 |
KE2 . |
(2.20) |
||
I 2 |
= c |
σ |
2 |
KE |
|
|
2 |
|
1 |
|
|
Если на поверхности образца присутствуют загрязнения (адсорбат) толщиной d, тогда:
I |
|
c1σ1 |
KE2 |
|
|
d |
− |
d |
|
|
|
|
− |
|
|
||||||
1 |
|
|
λ λ |
|
(2.21) |
|||||
|
= c2σ 2 |
|
e |
|
1 |
|
2 |
. |
||
I 2 |
KE1 |
|
|
|
|
|
|
|||
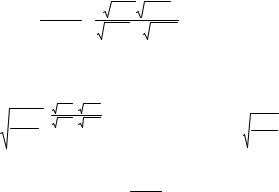
Обозначим λ1 = λ(KE1), λ2 = λ(KE2). Поскольку толщина адсорбата не превышает несколько атомных слоев, то для оценки положим d −1 = λ1−1 + λ−21 , откуда
48
|
|
d = |
λ1λ2 |
|
~ |
|
KE1 KE2 . |
(2.22) |
||||||
|
|
λ1 + λ2 |
KE + KE |
2 |
|
|
|
|||||||
Тогда имеем |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
I1 |
|
c1σ1 |
|
|
|
|
|
||||
|
|
|
|
= |
C , |
|
(2.23) |
|||||||
|
|
|
|
I |
2 |
|
c σ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
где C = C(E , E |
|
) = KE2 |
KE1 − |
KE2 |
|
|
|
|
|
KE2 |
|
|
||
2 |
e KE1 + |
KE2 . Введя обозначение |
=ξ |
, |
||||||||||
1 |
KE |
|
|
|
|
|
|
|
|
|
KE |
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
получим:
С= ξ exp 1−ξ .
1+ξ
Оценим вклад параметра C при характерных значениях кинети-
ческих |
энергий остовных |
электронов |
КE ~ 500÷1000 эВ. При |
ξ=E2/E1 = 1.5 величина С составляетC = 1.1, а при ξ=E2/E1 = 2.5 - |
|||
C = 1.25. |
Если КE1/КE2 < 2, |
то ошибка |
для с1/с2 не превосхо- |
дит 20÷30%. Следовательно, вклад этого параметра оказывается относительно малым, и тогда выражение (2.23) упрощается:
I1 |
≈ |
c1σ1 |
. |
(2.24) |
||
|
|
|||||
I |
2 |
|
c σ |
2 |
|
|
|
2 |
|
|
|||
Отметим, что выражение (2.24) тем точнее, чем ближе друг к другу значения КE1 и КE2. Отсюда
c |
= |
I |
1 |
σ 2 |
|
|
|
1 |
|
|
|
. |
(2.25) |
||
c |
I |
|
σ1 |
||||
|
2 |
|
|
|
|||
2 |
|
|
|
|
|
|
|
Для определения относительных сечений фотоионизации σ1/σ2 используют градуировочные кривые. Для их получения измеряют
зависимость I1 / I2 = f (σ1 / σ2 ) для эталонных многоэлементных
образцов с известными значениями концентраций с.
На практике же обычно используют так называемые значения факторов чувствительности S, известных для основных линий всех элементов и пропорциональных сечению фотоионизации. В этом случае интенсивность линии i-го элемента выражается в виде Ii = сi·Si. Значения факторов чувствительности, выражаемых в относительных единицах (обычно за S=1 принимают чувствительность к фтору F1s или углероду C1s) для ряда элементов представлены в табл. 2.2.
49