сывают состояние электрона в виде nlj (где для указания орбитального квантового числа l используются латинские буквы s, p, d, f и т.д. для l=0, 1, 2, 3...) и используется для обозначения фотоэлектронных линий в РФЭС. Рентгеновские обозначения, основанные на рентгеновских индексах и первоначально введенные для рентгеновской эмиссионной спектроскопии, используются для обозначения пиков оже-электронов как в методе РФЭС, так и в методе ОЭС.
Таблица 2.1. Рентгеновские и спектроскопические обозначения электронных уровней
Число |
Квантовые |
Рентгеновский |
Спектроскопическое |
Рентгеновское |
|||
электронов |
|
числа |
индекс |
обозначение уровня |
обозначение |
||
в оболочке |
|
|
|
|
(РФЭС) |
уровня (ОЭС) |
|
n |
l |
j |
|
||||
2 |
1 |
0 |
1/2 |
1 |
1s1/2 |
K |
|
6 |
2 |
0 |
1/2 |
1 |
2s1/2 |
L1 |
|
1 |
1/2 |
2 |
2p1/2 |
L2 |
|||
|
|
3/2 |
3 |
2p3/2 |
L3 |
||
|
|
|
|||||
|
|
0 |
1/2 |
1 |
3s1/2 |
M1 |
|
10 |
3 |
1 |
1/2 |
2 |
3p1/2 |
M2 |
|
3/2 |
3 |
3p3/2 |
M3 |
||||
|
|||||||
|
|
2 |
3/2 |
4 |
3d1/2 |
M4 |
|
|
|
5/2 |
5 |
3d3/2 |
M5 |
||
|
|
|
|||||
2.4. Количественный анализ спектров. Расчет интенсивности
Интенсивность рентгеновской фотоэлектронной линии зависит от нескольких факторов, что можно представить в следующем виде:
I = A·B·C, |
(2.6) |
здесь I — интенсивность (количество фотоэлектронов, испускаемых в единицу времени), A — характеристика процесса фотоионизации (вероятность ионизации атома рентгеновским излучением), B
— характеристика образца (длина свободного пробега фотоэлектронов в образце), C — аппаратный фактор (регистрация вылетевших из образца фотоэлектронов).
Рассмотрим каждую составляющую.
38
2.4.1. Характеристика процесса фотоионизации
Общее число фотоэлектронов, рождающихся при ионизации nl оболочки m атомов в объеме образца при его облучении рентгенов-
ским излучением с интенсивностью I0 есть |
|
N = I0mσnl . |
(2.7) |
Основной характеристикой процесса фотоионизации, определяющей интенсивность спектральной линии, является сечение фотоионизации.
Сечение фотоионизации σnl (hv) для свободного атома опре-
деляется вероятностью ионизации оболочки атома с квантовыми числами n и l при попадании одного фотона с энергией hv на поверхность образца единичной площади в единицу времени.
Сечение фотоионизации пропорционально квадрату матричного элемента перехода системы под действием фотона hν из
начального (initial) состояния i , описываемого волновой функци-
ей Ψi в конечное (final) ионизованное состояние |
f с волновой |
||||||||
функцией Ψf : |
|
|
|
|
|
|
|
|
|
σ |
|
~ |
Ψ |
|
ˆ |
|
2 |
, |
(2.8) |
|
|
|
|
||||||
nl |
f |
H Ψ |
|
||||||
|
|
|
|
i |
|
|
|
||
ˆ – гамильтониан взаимодействия фотона с электроном. В где H
простейшем случае вычисление сечения проводят в одноэлектронном приближении, записывая волновые функции Ψ в виде определителя Слэтера (суперпозиции одноэлектронных волновых функций) и полагая, что основной эффект фотоэмиссии сводится к воз-
буждению электрона из связанного состояния ϕnl в свободное состояние ϕph , тогда как остальные «пассивные» орбитали остаются неизменными. В этом случае можно записать:
ˆ |
2 |
ˆ |
2 |
2 |
|
|
Ψf (N −1) Ψi (N −1) . (2.9) |
||
Ψf H Ψi |
|
= ϕph H ϕnl |
|
Пренебрегая релаксацией электронной подсистемы в конечном состоянии («замороженные орбитали») получается следующее выражение для сечения фотоионизации [14]:
39
|
4πα a02 |
|
* G |
G |
|
2 |
|
|
|
|
|
|
|||||
σnl = |
|
hv |
∫ϕph r |
ϕnl dr |
|
, |
(2.10) |
|
3 |
||||||||
|
|
|
|
|
|
|
где α – постоянная тонкой структуры, а0 – радиус Бора. Для получения сечения фотоионизации для всей nl-подоболочки необходимо провести суммирование по всем конечным состояниям и усредне-
ние по всем орбиталям ϕnl (т.е. по двум возможным значениям
орбитального момента фотоэлектрона (l-1) и (l+1), определяющимся правилами отбора, и всем значениям магнитных квантовых чисел).
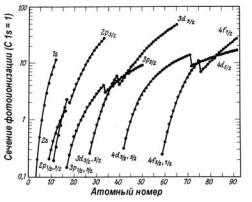
На рис.2.4 представлены расчетные зависимости сечения фотоионизации различных электронных оболочек атомов от атомного номера для ряда элементов при возбуждении рентгеновским излучением с энергией 1.5 кэВ.
Общее сечение фотоионизации представляет собой интегральную величину по всем углам испускания фотоэлектронов относительно направления распространения фотонов. Поскольку энергоанализатор спектрометра регистрирует лишь часть фотоэлектронов, испускаемых в направлении телесного угла Ω, определяемого геометрией спектрометра (диаметром входной щели анализатора электронов, расстоянием до образца и углом между направлением распространения фотонов и нормалью к поверхности образца (рис.2.5), необходимо знать угловую зависимость фотоэмиссии.
Рис. 2.4. Расчетные зависимости нормированного на сечение возбуждения С 1s сечения фотоионизации различных электронных оболочек атомов от атомного номера элемента при возбуждении рентгеновским излучением с энергией hv=1.5 кэВ. За единицу принято сечение фотоионизации оболочки 1s атома углерода [15]
40
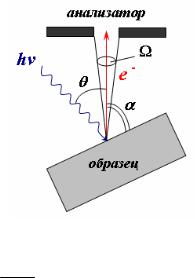
Рис. 2.5. Схематическое изображение геометрии спектрометра и образца при РФЭС: θ
– угол между направлением падающего рентгеновского излучения с энергией hv и вылетающего фотоэлектрона; α – угол поворота образца относительно входной щели анализатора; Ω – телесный угол, в направлении которого эмитировавшие фотоэлектроны попадают в энергоанализатор
Данную зависимость можно найти, используя понятие о диффе-
ренциальном сечении фотоионизации ddσΩnl , которое характеризует поток фотоэлектронов за единицу времени в телесный угол Ω [14]:
dσ |
nl |
|
σ |
nl |
|
|
1 |
3 |
sin 2 |
|
. |
(2.11) |
||
|
= |
|
1 |
+ |
|
β |
|
θ −1 |
|
|||||
|
|
|
|
|
|
|||||||||
dΩ |
4π |
|
|
2 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
Здесь величина β – параметр асимметрии, |
принимающий значения |
в интервале −1≤ β ≤ 2 , θ – угол между |
направлениями распро- |
странения фотона и фотоэлектрона. Параметр асимметрии зависит от орбитального момента, радиальных волновых функций электронных орбиталей начального и конечного состояния и зависящих от кинетической энергии фотоэлектрона фазовых сдвигов. Значение β > 0 указывает на то, что максимум интенсивности фотоэлектро-
нов приходится на θ = 90° , а отрицательные значения β свидетельствуют о преимущественной эмиссии в направлении, параллельном распространению фотонов. Для s-оболочки (l = 0) величина β = 2, для p-, d-, … оболочек (l = 1, 2, …) область изменения β определяется неравенством 1 ≤ β < 2. Так, для урана β = 0.86, а для лития
Li1s β = 2.
В итоге, для характеристики процесса фотоионизации получаем следующее выражение:
A = k |
σnl |
|
1 |
3 |
|
2 |
|
. |
(2.12) |
|||
|
1 |
+ |
|
β |
|
sin |
|
θ −1 |
|
|||
|
|
|
|
|||||||||
|
4π |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
41