
- •Министерство образования и науки Российской Федерации
- •Амурский государственный университет (фгбоу впо «АмГу»)
- •Курсовая работа
- •Министерство образования и науки Российской Федерации
- •Амурский государственный университет (фгбоувпо «АмГу») рецензия на курсовую работу
- •Министерство образования и науки Российской Федерации
- •Амурский государственный университет (фгбоу впо «АмГу»)
- •Задание
- •1.1 Сущность статистического изучения браков
- •1.2 Система статистических показателей, используемых в изучении браков
- •2.1 Анализ динамики браков
- •2.2 Анализ структуры браков в Амурской области
- •2.3 Группировка городов и районов Амурской области по числу браков за 2013 год
- •2.4 Анализ браков с помощью расчета средних величин и показателей вариации
- •2.5 Корреляционно – регрессионный анализ взаимосвязи между количеством браков и средним возрастом брачующихся
2.5 Корреляционно – регрессионный анализ взаимосвязи между количеством браков и средним возрастом брачующихся
Изучим влияние среднего возраста вступающих в брак на численность заключенных браков. Для этого используем данные таблиц 4 и 9.
Таблица 9 – Средний возраст вступающих в брак12
|
Год |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Возраст, лет |
26,5 |
26,1 |
25,3 |
24 |
24,8 |
22,7 |
21,9 |
22 |
22,2 |
22,6 |
На рисунке 4 изображена динамика среднего возраста вступающих в брак в Амурской области.

Рисунок 4 – Динамика среднего возраста вступающих в брак
Из рисунка видно, что за последние 10 лет средний возраст брачующихся в Амурской области снизился.
Для того, чтобы выяснить существование линейной зависимости между факторным признаком (средним возрастом брачующихся) и результативным (числом браков) построим линейное уравнение регрессии по формуле (26):
yx=a0+a1*x
Для определения формы корреляционной зависимости необходимо вычислить параметры уравнения прямой путем решения системы нормальных уравнений вида (27).
Для
того, чтобы заполнить систему нормальных
уравнений фактическими данными,
необходимо определить
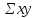 ,
, ,
, .
.
Расчеты этих показателей представим в форме таблицы.
Таблица 10 – Расчет сумм для вычисления параметров уравнения прямой по несгруппированным данным
|
Год |
X |
Y |
X2 |
Y2 |
XY |
Yx |
(Y-Yx) |
(Y-Yx)2 |
|
2004 |
26,5 |
5818 |
702,25 |
33849124 |
154177 |
6193,577 |
-375,577 |
141057,7 |
|
2005 |
26,1 |
5944 |
681,21 |
35331136 |
155138,4 |
6294,16 |
-350,16 |
122612,1 |
|
2006 |
25,3 |
6467 |
640,09 |
41822089 |
163615,1 |
6495,327 |
-28,3273 |
802,4359 |
|
2007 |
24 |
7288 |
576 |
53114944 |
174912 |
6822,224 |
465,776 |
216947,3 |
|
2008 |
24,8 |
7449 |
615,04 |
55487601 |
184735,2 |
6621,057 |
827,9432 |
685489,9 |
|
2009 |
22,7 |
6781 |
515,29 |
45981961 |
153928,7 |
7149,121 |
-368,121 |
135512,8 |
|
2010 |
21,9 |
6894 |
479,61 |
47527236 |
150978,6 |
7350,288 |
-456,288 |
208198,6 |
|
2011 |
22 |
7071 |
484 |
49999041 |
155562 |
7325,142 |
-254,142 |
64588,16 |
|
2012 |
22,2 |
7629 |
492,84 |
58201641 |
169363,8 |
7274,85 |
354,1498 |
125422,1 |
|
2013 |
22,6 |
7359 |
510,76 |
54154881 |
166313,4 |
7174,267 |
184,7334 |
34126,43 |
|
Итого |
238,1 |
68700 |
5697,09 |
475469654 |
1628724 |
68700,01 |
-0,0121 |
1734758 |
Подставив в систему (27) данные из таблицы и, проведя простейшие преобразования, получим:
a0=
 =12857,24;
=12857,24;
а1
=
 = -251,459.
= -251,459.
Уравнение регрессии имеет вид:
ух=12857,24 – 251,459х
Анализируя полученное уравнение регрессии, можно сделать вывод, что с увеличением среднего возраста брачующихся на 1 год число браков снижается на 251,459. Параметр а0 = 12857,24 показывает влияние на результативный признак неучтенных факторов.
Используя уравнение корреляционной связи, можно вычислить теоретические значения ух для любой промежуточной точки. Расчеты представлены в таблице 10.
Учитывая, что суммы теоретических (уx) и эмпирических (у) значений числа браков практически равны друг другу, а сумма разностей между ними примерно равна нулю, параметры регрессионного уравнения определены верно.
На рисунке 5 изображена зависимость между теоретическими значениями ух и значениями факторного признака.

Рисунок 5 – Зависимость количества браков от среднего возраста брачующихся
Измерить тесноту корреляционной связи между факторным и результативным признаками позволяет линейный коэффициент корреляции (r) (28):
r
=
 = -0,71
= -0,71
По абсолютной величине коэффициент корреляции близок к единице, следовательно между средним возрастом вступающих в брак и количеством браков сильная зависимость.
Далее
рассчитаем теоретическое корреляционное
отношение ( )
(32).
)
(32).
Для его расчета необходимо предварительно вычислить дисперсии по формулам (29)-(31).
Общая дисперсия (29):
 =
=
 - (6870)2
= 350065,4
- (6870)2
= 350065,4
Остаточная дисперсия (30):
 =
=
 = 173475,8
= 173475,8
Факторная дисперсия (31):
 =
350065,4-173475,8 = 176589,6
=
350065,4-173475,8 = 176589,6
Теоретическое корреляционное отношение (32):
 =
=
 = 0,71
= 0,71
Полученный результат указывает на достаточную тесноту связи между результативным и факторным признаками.
Рассчитаем индекс корреляционной связи (R) по формуле (33):
R=
 = 0,71
= 0,71
Далее вычислим коэффициент детерминации по формуле:
 =
=
 *100
% = (-0,71)2*100
% = 50,41 %
*100
% = (-0,71)2*100
% = 50,41 %
Анализируя полученный результат, можно сказать, что число браков на 50,41 % зависит от среднего возраста брачующихся и на 49,59 % от остальных факторов.
Найдем значение частного коэффициента эластичности (34):
Э
= -251,459* = -0,8715 или -87,15 %
= -0,8715 или -87,15 %
Видим, что при изменении среднего возраста вступающих в брак на 1 % число браков изменится на 87,15 %.
Адекватность регрессионной модели yx=a0+a1*x при малой выборке оценим критерием Фишера (35):
Fэ
=
 *
* = 8,1436
= 8,1436
Сравнивая полученное эмпирическое значение критерия при уровне значимости 0,05 и числе степеней свободы 1 и 8, получим:
Fэ= 8,1436 > Fт= 5,32
Следовательно, уравнение регрессии признается адекватным (значимым).
Значимость коэффициентов линейного уравнения регрессии оценим с помощью критерия Стьюдента по формулам (36), (37), (38):
 =
=
 = 87,31
= 87,31
 =
=
 *
1,6712 = -2,8538
*
1,6712 = -2,8538
 =
=
 = 1,6712
= 1,6712
При
уровне значимости 0,05 и степени свободы
k1
=
8 табличное значение t-критерия Стьюдента
tт
= 2,31. Так как
 >
> >
> ,
то параметр
,
то параметр признается значимым, а параметр
признается значимым, а параметр -
не адекватным.
-
не адекватным.
Аналогично оценим коэффициент корреляции с помощью t-критерия (39):
 =
-0,71*
=
-0,71* = -2,8517
= -2,8517
Так как tэ = -2,8517 < tт = 1,78, то коэффициент корреляции признается незначимым.
На заключительном этапе анализа вычислим ошибку аппроксимации (40):
 =
0,1*0,530842*100 % = 5,3 %
=
0,1*0,530842*100 % = 5,3 %
Ошибка аппроксимации не превышает 12 – 15 %, что свидетельствует о правильном подборе факторного признака, о точном проведении всех расчетов.
Делая вывод по проделанной работе, можно сказать, что данная модель может быть использована для анализа зависимости числа браков от среднего возраста брачующихся.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе были рассмотрены основные положения статистики браков. Были изучены базовые теоретические сведения, произведен расчет основных показателей брачности.
Цели, намеченные в начале выполнения курсовой работы, были достигнуты и были выполнены поставленные задачи.
Подведем итоги.
Анализируя динамику браков в Амурской области за 2004 – 2013 годы, можно убедиться в том, что число браков за 2004 – 2013 годы увеличилось, но за период с 2008 по 2009 год произошло снижение числа браков. Главным образом такая динамика сложилась под влиянием брачной обстановки среди сельского населения.
Анализ структуры браков в Амурской области показал, что доля городского населения в общем числе браков намного превосходит долю сельского населения.
Группировка городов и районов Амурской области указывает на то, что в 89,29 % муниципальных образований число браков не превышает 436.
Анализируя выполненную работу в целом, можно увидеть, что ситуация с заключением браков в Амурской области нуждается в исправлении. Снижение числа браков, уменьшение доли браков среди сельского населения, уменьшение среднего возраста брачующихся – это лишь небольшой перечень проблем, имеющих место в брачной системе Амурской области.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1 Амурский статистический ежегодник: Сборник/Амурстат., 2013. – 503с.
2 Конина, М.М. Социально - экономическая статистика / М.М. Конина. - М.: Финансы и статистика, 2010. – 368 с.
3 Синельников, А.Б. Специфика брачности и разводимости в России /А.Б. Синельников. – Ростов-на-Дону: Феникс, 2012. – 202 с.
4 Теслюк, И.Е.Социально - экономическая статистика / И.Е. Теслюк, С.С. Подхватилина.- Н.Н.: БГДУ, 2002. – 239 с.
5 Тольц, М.С. Некоторые обобщающие характеристики брачности, прекращения и длительности брака / М.С. Тольц. – М.:ИНФРА, 2002. – 247 с.
6 Иванова, Е.И. Браки и разводы /Е.И. Иванова. – М.: ИНФРА,2004. – 198 с.
7 Архангельский, В.Н. Система показателей для анализа демографической ситуации /В.Н. Архангельский. – М.: КНОРУС, 2003. – 302 с.
ПРИЛОЖЕНИЕ А
Таблица А.1 – Динамика браков и разводов в Амурской области
|
Годы |
|
Число браков |
|
|
Число разводов | |
|
Все население |
Городское население |
Сельское население |
Все население |
Городское население |
Сельское население | |
|
1970 |
6543 |
4361 |
2182 |
842 |
749 |
93 |
|
1971 |
6970 |
4718 |
2252 |
1630 |
1326 |
304 |
|
1972 |
7563 |
4936 |
2627 |
2129 |
1709 |
420 |
|
1973 |
8478 |
5460 |
3018 |
2265 |
1887 |
378 |
|
1974 |
8875 |
5652 |
3223 |
2048 |
1619 |
429 |
|
1975 |
9252 |
5917 |
3335 |
2101 |
1730 |
371 |
|
1976 |
9877 |
6323 |
3554 |
2061 |
1667 |
394 |
|
1977 |
9383 |
6179 |
3204 |
2316 |
1924 |
392 |
|
1978 |
9796 |
6296 |
3500 |
2354 |
1953 |
401 |
|
1979 |
10321 |
6622 |
3699 |
2712 |
2192 |
520 |
|
1980 |
10644 |
6735 |
3909 |
2974 |
2348 |
626 |
|
1981 |
11108 |
7078 |
4030 |
3669 |
2917 |
752 |
|
1982 |
11609 |
7160 |
4449 |
4212 |
3296 |
916 |
|
1983 |
11212 |
7136 |
4076 |
4164 |
3130 |
1034 |
|
1984 |
11262 |
7014 |
4248 |
4307 |
3216 |
1091 |
|
1985 |
10668 |
6489 |
4179 |
4039 |
2894 |
1145 |
|
1986 |
10519 |
6571 |
3948 |
4024 |
2900 |
1124 |
|
1987 |
10400 |
6600 |
3800 |
3961 |
2930 |
1031 |
|
1988 |
10363 |
6818 |
3545 |
4089 |
2992 |
1097 |
|
1989 |
9493 |
6010 |
3483 |
4234 |
3001 |
1233 |
|
1990 |
9760 |
6183 |
3577 |
4092 |
3120 |
972 |
|
1991 |
10315 |
7088 |
3227 |
4478 |
3285 |
1193 |
|
1992 |
10402 |
7186 |
3216 |
4608 |
3464 |
1144 |
|
1993 |
10561 |
7492 |
3069 |
4444 |
3296 |
1148 |
|
1994 |
10771 |
7532 |
3239 |
4541 |
3345 |
1196 |
|
1995 |
10045 |
7060 |
2985 |
4148 |
3112 |
1036 |
|
1996 |
9839 |
6905 |
2934 |
4603 |
3391 |
1212 |
|
1997 |
7642 |
5289 |
2353 |
5024 |
3717 |
1307 |
|
1998 |
7824 |
5366 |
2458 |
5272 |
3881 |
1391 |
|
1999 |
7686 |
5399 |
2287 |
5342 |
3964 |
1378 |
|
2000 |
7434 |
5295 |
'2139 |
5114 |
3900 |
1214 |
|
2001 |
5877 |
4168 |
1709 |
4284 |
3244 |
1040 |
|
2002 |
6198 |
4404 |
1794 |
4099 |
3103 |
996 |
|
2003 |
5510 |
3984 |
1526 |
3617 |
2766 |
851 |
|
2004 |
5818 |
4231 |
1587 |
3085 |
2382 |
703 |
|
2005 |
5944 |
4323 |
1621 |
3806 |
2884 |
922 |
|
2006 |
6467 |
4735 |
1731 |
4941 |
3782 |
1159 |
|
2007 |
7288 |
5269 |
2019 |
6109 |
4621 |
1488 |
|
2008 |
7449 |
5684 |
1765 |
5591 |
4526 |
1065 |
|
2009 |
6781 |
5421 |
1360 |
4447 |
'3714 |
733 |
|
2010 |
6894 |
5609 |
1285 |
4167 |
3525 |
642 |
|
2011 |
7071 |
5824 |
1247 |
4533 |
3810 |
723 |
|
2012 |
7629 |
6311 |
1318 |
5079 |
4204 |
875 |
|
2013 |
7359 |
6190 |
1169 |
5062 |
4282 |
780 |
ПРИЛОЖЕНИЕ Б
Таблица Б.1 – Числобраков в городах и районах Амурской области в 2013 году
|
№ группы |
Название муниципального образования |
Число браков, ед. |
|
1 |
г. Тында |
381 |
|
2 |
Благовещенский |
16 |
|
3 |
Завитинский |
148 |
|
4 |
Ромненский |
68 |
|
5 |
Мазановский |
109 |
|
6 |
Октябрьский |
155 |
|
7 |
Архаринский |
111 |
|
8 |
Селемжинский |
69 |
|
9 |
Белогорский |
61 |
|
10 |
Свободненский |
64 |
|
11 |
Тындинский |
71 |
|
12 |
Магдагачинский |
172 |
|
13 |
Шимановский |
4 |
|
14 |
Константиновский |
87 |
|
15 |
Зейский |
72 |
|
16 |
Ивановский |
198 |
|
17 |
Михайловский |
91 |
|
18 |
Сковородинский |
256 |
|
19 |
г. Райчихинск |
200 |
|
20 |
Серышевский |
188 |
|
21 |
Бурейский |
202 |
|
22 |
г. Шимановск |
188 |
|
23 |
пгт Прогресс |
100 |
|
24 |
Тамбовский |
197 |
|
25 |
г.Зея |
308 |
|
26 |
г. Белогорск |
677 |
|
27 |
г. Свободный |
584 |
|
28 |
Благовещенск |
2601 |
1 Конина М.М. Социально - экономическая статистика М.: Финансы и статистика, 2010. 368 с.
2Конина М.М. Социально - экономическая статистика М.: Финансы и статистика, 2010. 368с.
3Синельников А.Б. Специфика брачности и разводимости в России Ростов-на-Дону: Феникс, 2012. 202 с.
4Теслюк И.Е. Социально - экономическая статистика Н.Н.: БГДУ, 2002. 239 с.
5Конина М.М. Социально - экономическая статистика М.: Финансы и статистика, 2010. 368с.
6Иванова Е.И. Браки и разводы М.: ИНФРА,2004. 198 с.
7Синельников А.Б. Специфика брачности и разводимости в России. Ростов-на-Дону: Феникс, 2003. 202 с.
8Тольц М.С. Некоторые обобщающие характеристики брачности, прекращения и длительности брака М.:ИНФРА, 2002. 247 с.
9Архангельский В.Н. Система показателей для анализа демографической ситуации. М.: КНОРУС, 2003. 302 с.
10Там же
11Амурский статистический ежегодник: Сборник/Амурстат., 2013. – 503с.
12Амурский статистический ежегодник: Сборник/Амурстат., 2013. – 503с.
