Интегральная теорема Лапласа

Предположим, что проводится  независимых испытаний, в каждом из которых вероятность появления события  постоянна и равна . Необходимо вычислить вероятность того, что событие  появится в  испытаниях не менее  и не более  раз (для краткости будем говорить "от  до  раз"). Это можно сделать с помощью интегральной теоремы Лапласа.

Теорема 3.2. Если вероятность  наступления события  в каждом испытании постоянна и отлична от нуля и единицы, то приближенно вероятность  того, что событие появится в испытаниях от  до  раз,

 где .

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл  не выражается через элементарные функции. Таблица для интеграла 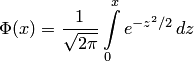 приведена в прил. 2, где даны значения функции  для положительных значений , для  используют ту же таблицу (функция  нечетна, т. е. ). Таблица содержит значения функции  лишь для ; для  можно принять .

Итак, приближенно вероятность того, что событие  появится в  независимых испытаниях от  до  раз,

 где .

Пример 4. Вероятность того, что деталь изготовлена с нарушениями стандартов, . Найти вероятность того, что среди 400 случайно отобранных деталей нестандартных окажется от 70 до 100 деталей.

Решение. По условию . Воспользуемся интегральной теоремой Лапласа:

Вычислим пределы интегрирования:

нижний

верхний

Таким образом

По таблице прил. 2 находим

Искомая вероятность

Применение интегральной теоремы Лапласа

Если число  (число появлений события  при  независимых испытаниях) будет изменяться от  до , то дробь  будет изменяться от  до . Следовательно, интегральную теорему Лапласа можно записать и так:

(3.6)

Поставим задачу найти вероятность того, что отклонение относительной частоты  от постоянной вероятности  по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства , что то же самое, . Эту вероятность будем обозначать так: . С учетом формулы (3.6) для данной вероятности получаем

(3.7)

Пример 5. Вероятность того, что деталь нестандартна, . Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности  по абсолютной величине не более чем на 0,03.

Решение. По условию . Требуется найти вероятность . Используя формулу (3.7), получаем

По таблице прил. 2 находим , следовательно, . Итак, искомая вероятность приближенно равна 0,9544. Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности  по абсолютной величине не превысит 0,03.

Формула Пуассона для маловероятных событий

Если вероятность  наступления события в отдельном испытании близка к нулю, то даже при большом числе испытаний , но при небольшом значении произведения  получаемые по формуле Лапласа значения вероятностей  оказываются недостаточно точными и возникает потребность в другой приближенной формуле.

Теорема 3.3. Если вероятность  наступления события  в каждом испытании постоянна, но мала, число независимых испытаний  достаточно велико, но значение произведения остается небольшим (не больше десяти), то вероятность того, что в этих испытаниях событие  наступит  раз,

Для упрощения расчетов с применением формулы Пуассона составлена таблица значений функции Пуассона  (см. прил. 3).

Пример 6. Пусть вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.

Решение. Здесь . Все три числа удовлетворяют требованиям теоремы 3.3, поэтому для нахождения вероятности искомого события  применяем формулу Пуассона. По таблице значений функции Пуассона (прил. 3) при  получаем .

Найдем вероятность того же события по формуле Лапласа. Для этого сначала вычисляем значение , соответствующее :

Поэтому согласно формуле Лапласа искомая вероятность

а согласно формуле Бернулли точное ее значение

Таким образом, относительная ошибка вычисления вероятностей  по приближенной формуле Лапласа составляет

, или 

а по формуле Пуассона — 

, или 

т. е. во много раз меньше.