Наивероятнейшее число появлений события

Наивероятнейшим числом появления события  в  независимых испытаниях называется такое число , для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события . Для определения наивероятнейшего числа не обязательно вычислять вероятности возможных чисел появлений события, достаточно знать число испытаний  и вероятность появления события  в отдельном испытании. Обозначим  вероятность, соответствующую наивероятнейшему числу . Используя формулу (3.2), записываем

(3.3)

Согласно определению наивероятнейшего числа, вероятности наступления события  соответственно  и  раз должны, по крайней мере, не превышать вероятность , т. е.

Подставляя в неравенства значение  и выражения вероятностей  и , получаем

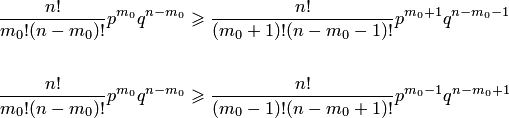
Решая эти неравенства относительно , получаем

Объединяя последние неравенства, получаем двойное неравенство, которое используют для определения наивероятнейшего числа:

(3.4)

Так как длина интервала, определяемого неравенством (3.4), равна единице, т. е.

и событие может произойти в  испытаниях только целое число раз, то следует иметь в виду, что: 1) если  — целое число, то существуют два значения наивероятнейшего числа, а именно:  и ;

2) если  — дробное число, то существует одно наивероятнейшее число, а именно: единственное целое, заключенное между дробными числами, полученными из неравенства (3.4);

3) если  — целое число, то существует одно наивероятнейшее число, а именно: .

При больших значениях  пользоваться формулой (3.3) для расчета вероятности, соответствующей наивероятнейшему числу, неудобно. Если в равенство (3.3) подставить формулу Стирлинга

справедливую для достаточно больших , и принять наивероятнейшее число , то получим формулу для приближенного вычисления вероятности, соответствующей наивероятнейшему числу: (3.5)

Пример 2. Известно, что  часть продукции, поставляемой заводом на торговую базу, не удовлетворяет всем требованиям стандарта. На базу была завезена партия изделий в количестве 250 шт. Найти наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, и вычислить вероятность того, что в этой партии окажется наивероятнейшее число изделий.

Решение. По условию . Согласно неравенству (3.4) имеем

откуда . Следовательно, наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, в партии из 250 шт. равно 234. Подставляя данные в формулу (3.5), вычисляем вероятность наличия в партии наивероятнейшего числа изделий:

Локальная теорема Лапласа

Пользоваться формулой Бернулли при больших значениях  очень трудно. Например, если , то для отыскания вероятности  надо вычислить значение выражения

Естественно, возникает вопрос: нельзя ли вычислить интересующую вероятность, не используя формулу Бернулли? Оказывается, можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления событий ровно  раз в  испытаниях, если число испытаний достаточно велико.

Теорема 3.1. Если вероятность  появления события  в каждом испытании постоянна и отлична от нуля и единицы, то вероятность  того, что событие  появится в  испытаниях ровно  раз, приближенно равна (тем точнее, чем больше ) значению функции

 при .

Существуют таблицы, которые содержат значения функции , соответствующие положительным значениям аргумента . Для отрицательных значений аргумента используют те же таблицы, так как функция  четна, т. е. .

Итак, приближенно вероятность того, что событие  появится в  испытаниях ровно  раз,

 где .

Пример 3. Найти вероятность того, что событие  наступит ровно 80 раз в 400 испытаниях, если вероятность появления события  в каждом испытании равна 0,2.

Решение. По условию . Воспользуемся асимптотической, формулой Лапласа:

Вычислим определяемое данными задачи значение :

По таблице прил, 1 находим . Искомая вероятность

Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):