4.2.1 Определение траектории движения точки

Уравнения движения являются одновременно уравнениями траектории точки в параметрической форме. Для получения уравнения траектории из уравнений движения необходимо исключить параметр t :

sin (t ) = ; cos (t ) = . (1)

Если обе части каждого равенства возвести в квадрат и сложить, то получим уравнение эллипса:

– = 1. (2)

Горизонтальная полуось эллипса = 2 м, вертикальная полуось эллипса b = 4 м, а координаты его центра = 3 м; = 0. Траекторию точки строим в масштабе на рисунке (рисунок 3).

4.2.2 Определение положения точки на траектории

Для определения положения точки на траектории в уравнения ее координат подставляем соответствующее время.

В начальный момент времени при t = 0 из этих уравнений получим:

= 3 м , = 4 м.

В заданный момент времени при = 1 c:

= 2 sin + 3 = 4,4 м ;

= 4 cos = 2,8 м.

По вычисленным координатам показываем положения точек ,

на траектории (рисунок 3).

3.3.2.3 Определение скорости и ускорения точки

Скорость и ускорение точки найдем по их проекциям на оси координат

; ; (3)

; . (4)

Тогда начальный момент времени при t = 0 получим:

м/с;;

= 1,57 м/с .;м/;

.

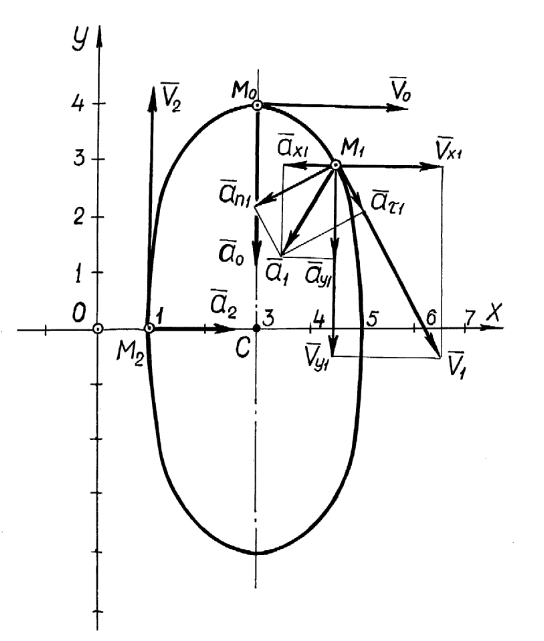
Рисунок 3

В заданный момент времени при : ; ;

;

; ;

.

Выбираем масштаб скорости и ускорения и строим векторы скорости и ускорения и их проекции для точек (рисунок 46). Величину выбранного масштаба необходимо указать на рисунке.

4.2.4 Определение касательного, нормального ускорения точки

и радиуса кривизны траектории

При движении точки по криволинейной траектории ускорение точки можно выразить через проекции на естественные оси: касательную и нормаль ,

где - касательное ускорение точки

; (5)

- нормальное ускорение ; (6)

где - радиус кривизны траектории.

Нормальное ускорение можно вычислить, зная полное ускорение точки и его касательную составляющую

. (7)

Подставляем в формулы (3.17), (3.18), (3.19) значения величин, найденных для соответствующих моментов времени. В начальный момент времени при :

; ;

.

В заданный момент времени при :

; ;

.

В выбранном масштабе ускорений показываем проекции ускорения точек на естественные оси координат (рисунок 46), что позволяет осуществить проверку решения.

На графике необходимо иметь соблюдение условия:

.

1. Пример решения задачи К2

Механизм состоит из ступенчатых колес 1 и 2, связанных между собой ременной передачей, колеса 2 и 3 находятся в зацеплении, колесо 1 находится в зацеплении с зубчатой рейкой 4, груз 5 находится на конце нити, намотанной на шкив 3 радиуса (рисунок 4).

Определить скорости точек В и С, ускорение груза 5, ускорение точки А и угловое ускорение колеса 2 в момент времени t = 2 c, если заданы закон движения рейки

и размеры колес

Решение

1. Рейка 4 совершает поступательное движение по закону

Определим скорость движения рейки .

При

Ускорение рейки найдем из соотношения .

Знак ускорения не совпадает со знаком скорости, следовательно, рейка движется замедленно.

2. Точка К, лежащая на ободе колеса , движется со скоростью,

равной скорости рейки, находящейся в зацеплении с колесом, т.е.

Учитывая, что , определим угловую скорость колеса 1:

.

При .

Определим угловое ускорение колеса 1: .

Ускорение точки А ступенчатого колеса 1найдем из выражения :

, Скорость точки С, лежащей на ободе колеса 3 радиуса , находим по формуле: .

5.Ускорение груза 5 равно касательному ускорению точки N колеса 3:

.

6. Найденные параметры движения точек и звеньев механизма изображаем на рисунке (рисунок 4).

где .

.

.

Рисунок 4

3. Колеса радиусов и связаны бесконечным ремнем. При отсутствии проскальзывания скорости всех точек ремня одинаковы, т.е.

а угловые скорости и угловые ускорения валов 1 и 2 обратно пропорциональны радиусам колес:

, тогда

;

Скорость точки В, лежащей на ободе колеса 2, рассчитываем по формуле

.

4. Колеса радиусов и находятся в зацеплении друг с другом, поэтому угловую скорость и угловое ускорение колеса 3 найдем из соотношений:

; .