1.20. Центр тяжести твердого тела.

Центром тяжести твердого тела называется точка, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела при любом положении тела в пространстве. Силы тяжести отдельных частиц тела образуют систему параллельных сил. Координаты центра тяжести как центра параллельных сил можно определить по формулам:

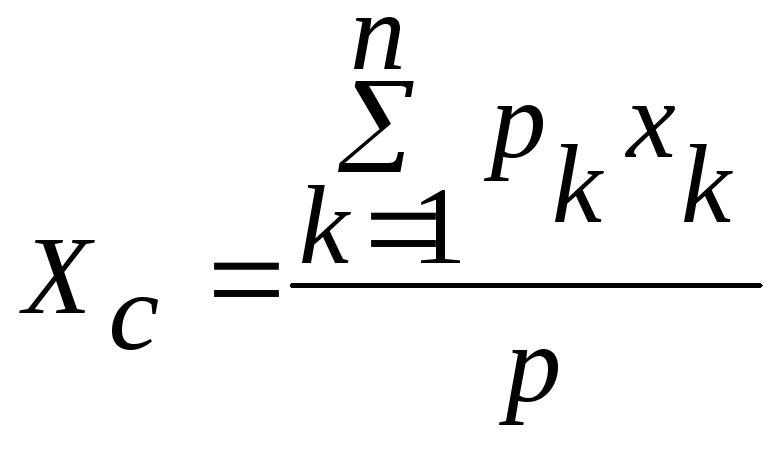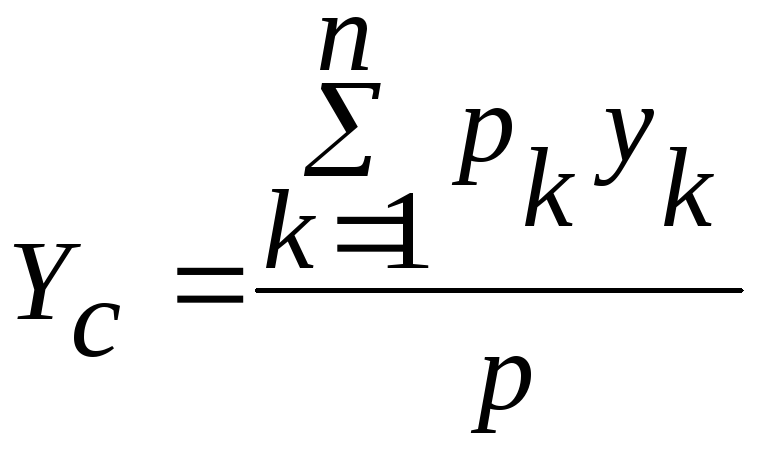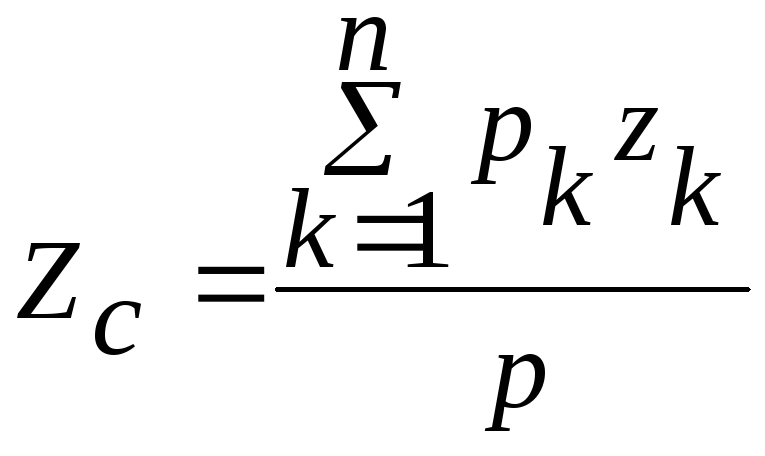; ;; (20.1)

где ,,- координаты точек приложенных сил тяжести частиц тела.

Положение центра тяжести однородного тела зависит только от геометрической формы тела. Координаты центра тяжести пластины определятся формулами:

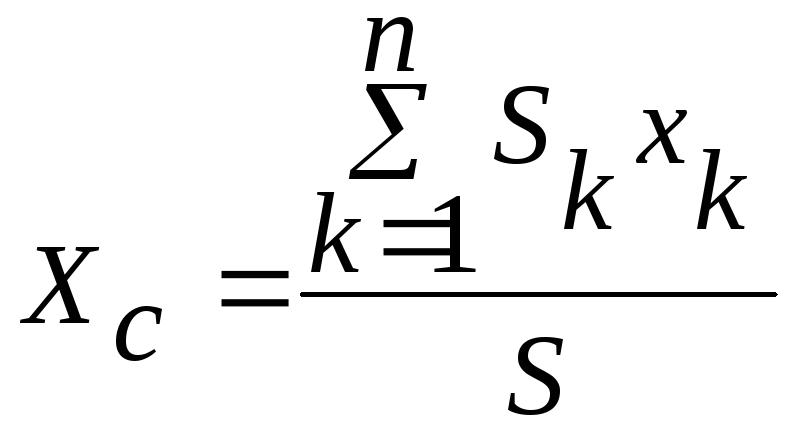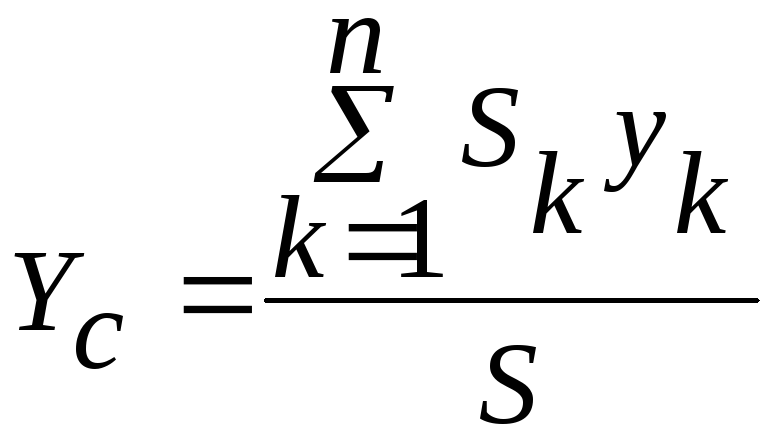; , (20.2)

где - площадь всей пластины;

- площадь части пластины.

Аналогично можно выразить координаты центра тяжести линии:

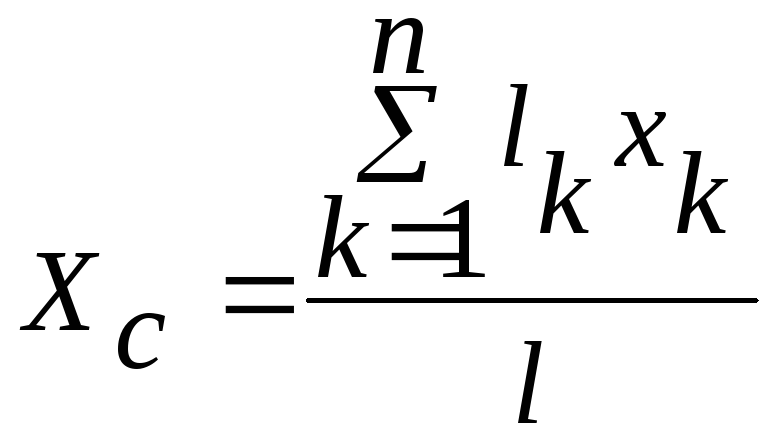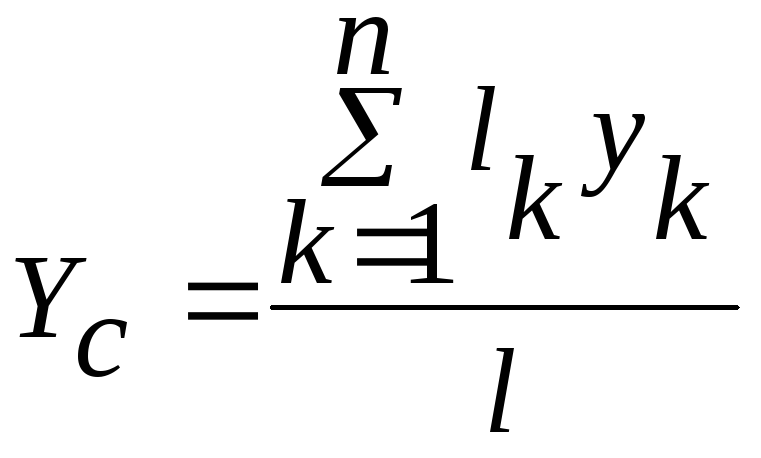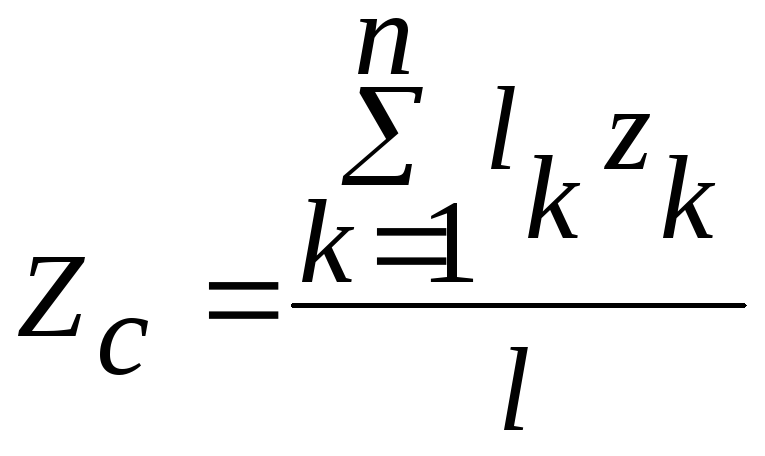; ;, (20.3)

где - длина всей линии;

- длина участка линии.

При определении координат центра тяжести тела плоской формы, тело разбивают на конечное число частей, для каждой из которых положение центра тяжести известно и используют формулы (20.2) или (20.3). Например, координаты центра тяжести пластины, изображенной на рис.48, можно определить двумя способами:

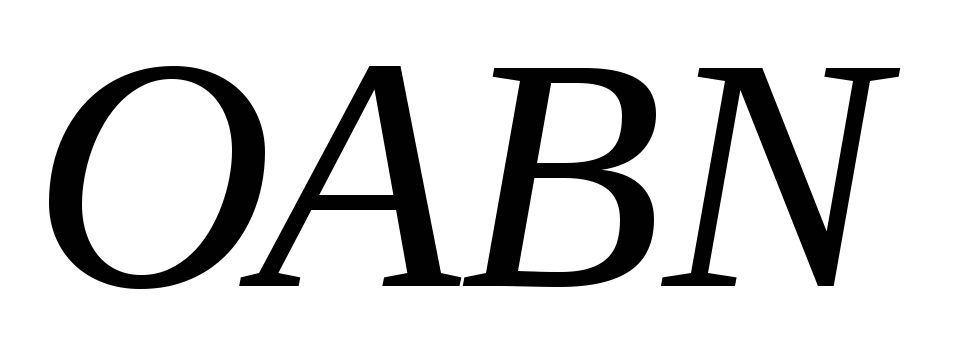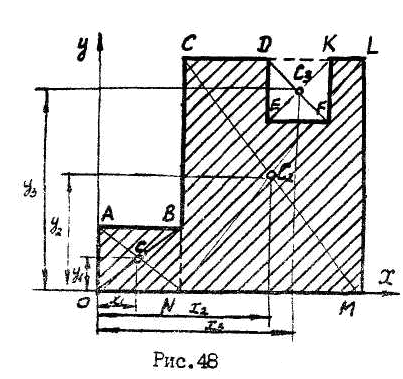
1. Разбить пластину на прямоугольники ,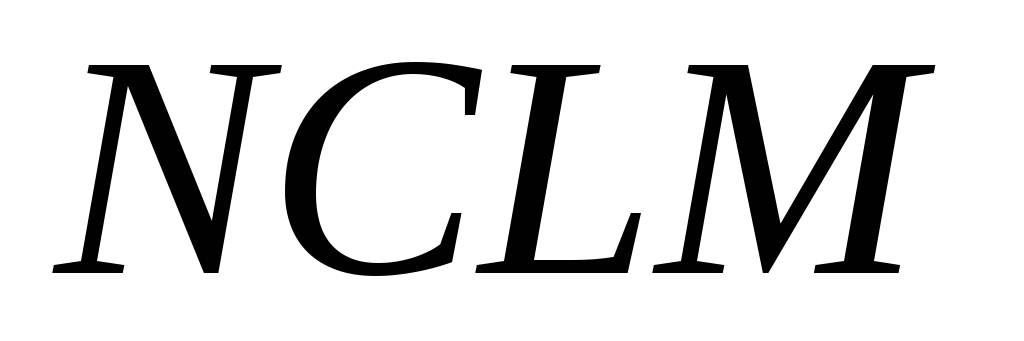и вырез. Тогда

;

;

где ,,- площади частей пластины и выреза.

2. Можно было рассмотреть пластину , и из нее вычесть два вырезаи.

Тогда

;

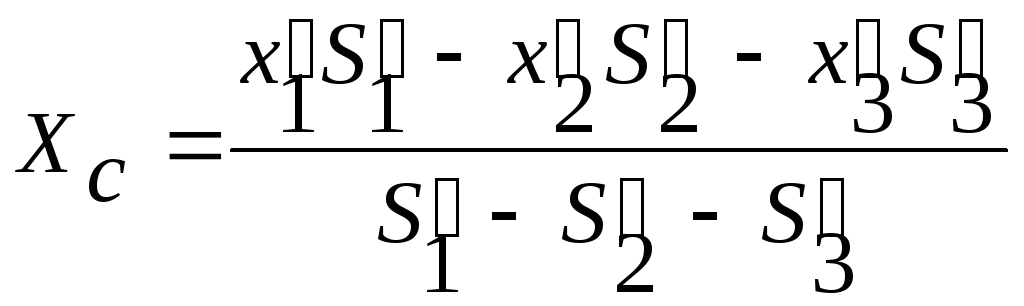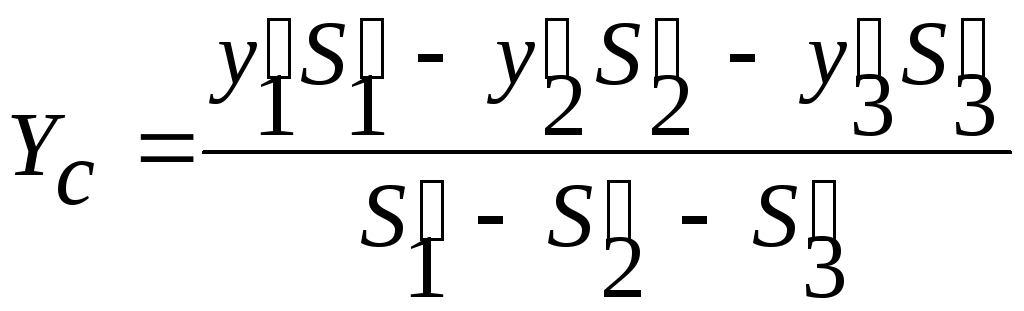
Центры тяжести некоторых однородных тел.

Центр тяжести дуги окружности в силу симметрии лежит на оси

с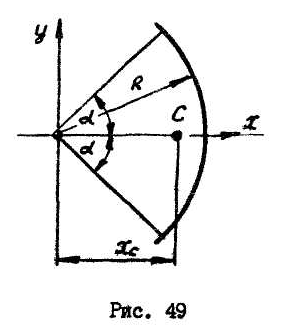имметрии (рис.49) и имеет координату:

, (20.4)

где - угол, измеряемый в радианах.

Центр тяжести площади кругового сектора лежит на оси

с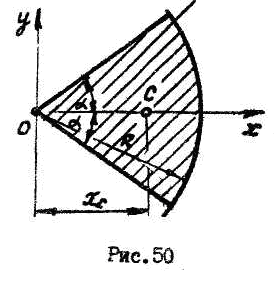имметрии (рис.50) и имеет координату:

. (20.5)

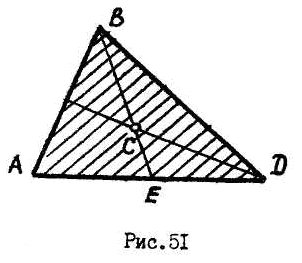
Центр тяжести треугольника лежит в точке пересечения медиан:

.

Пример №12.

Определить положение центра тяжести автокрана и статические нагрузки на его передний и заднийспаренные колесные хода, если общая масса автокрана, масса шасси; масса стрелы; кабины крановщика с поворотным устройством. Размеры приведены на рис.52а.

Р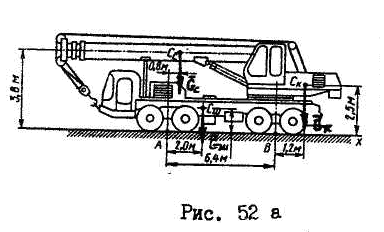ешение:

Данные для определения координат центра тяжести сведены в табл. 2.

Элемент	Масса ,	Координаты центра тяжести
		,		,
Кабина крановщика с поворотным устройством	4,8	7,6	2,5		36,48	12,0
Шасси	7,2	2,0	1,4		14,4	10,08
Стрела	4,0	0,8	3,8		3,2	15,2
Сумма	16,0				54,08	37,28

;

.

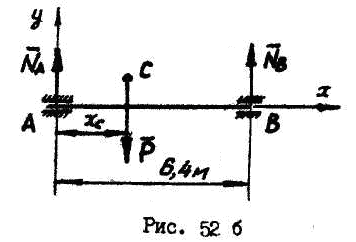
Для определения статических нагрузок на передний и заднийспаренные колесные хода составим расчетную схему (рис.52б). Для плоской системы параллельных сил составим два уравнения равновесия:

(1)

(2)

Тогда

из (2):

из (1):

2. К И Н Е М А Т И К А

2.1. Предмет и задачи кинематики.

Кинематика - раздел механики, который изучает геометричес­кие свойства механического движения тел без учета их массы и причин, вызывающих движение. Под механическим движением понима­ется происходящее с течением времени перемещение точек и тел в пространстве. При движении твердого тела его точки могут дви­гаться различно, поэтому изучение кинематики начинается с изу­чения-движения самого простого объекта - материальной точки.

Положение точки в пространстве определяется относительно системы отсчета, за которую может быть принято какое-то твердое тело и связанная с ним система координат.

Задачи, решаемые методами кинематики точки, можно разде­лить на следующие типы:

1. определение траектории движения точки;

2. определение скорости и ускорения точки по заданному закону движения - прямая задача кинематики;

3. определение закона движения точки в выбранной системе отсче­та - обратная задача кинематики.

0. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.

Определить движение точки - это значит определить положе­ние этой точки в любой момент времени по отношению к выбранной системе отсчета.

Кривая, которую описывает точка при своем движении в про­странстве относительно выбранной системы отсчета, называется траекторией (рис. 53,54).

Движение точки можно задать векторным, координатным и естественным способами.

При векторном способе положение точки задается радиусом - вектором , проведенным из некоторой неподвижной точки О (рис. 55). Каждому моменту времени соответствует новое значение радиуса – вектора . Следовательно, для векторного способа задания движения уравнение движения точки имеет вид:

(2.1)

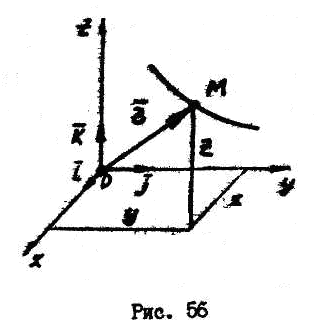
В декартовой системе координат (рис.56) положение точки определяется тремя ее координатами, изменяющимися во времени. Тогда в координатной форме уравнения движения точки будут иметь следующий вид:

, ,(2.2)

Если точка движется в плоскости , будем иметь два уравнения движения:

, (2.3)

При прямолинейном движении точки прямую, по которой движется точка принимаем за ось координат. Уравнение движения точки имеет вид:

. (2.4)

Между векторным и координатным способами задания движения су­ществует непосредственная связь. Координаты точки являются проекциями на оси координат, ее радиуса-вектора , а сам ра­диус-вектор можно определить через его проекции на координат­ные оси:

, (2.5)

где ,, - орты координатных осей , ,.

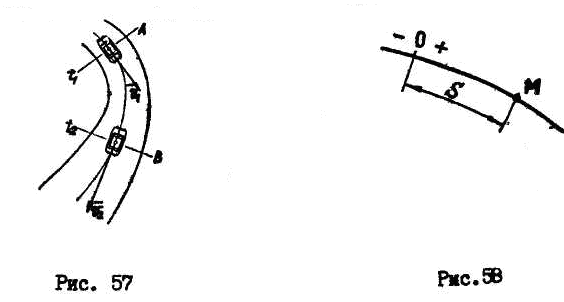
Естественный способ задания движения точки используется, если точка движется по криволинейной траектории (рис. 57). В этом случае для точки должны быть известны траектория движения, начало отсчета, направление отсчета.

Принимая за начало отсчета точку и выбрав положительное нап­равление отсчета, положение точки в любой момент времени можно определить дуговой координатой , которая изменяется с течением времени (рис.58).

Уравнение движения точки в естественной форме будет иметь вид:

. (2.6)

Взаимосвязь между координатным и естественным способами задания движения точки можно установить через дифференциал дуговой координаты:

, (2.7)

где ,,- дифференциалы координат точек;

, ,(2.8)

После интегрирования (2.7) в интервале времени от дополучим:

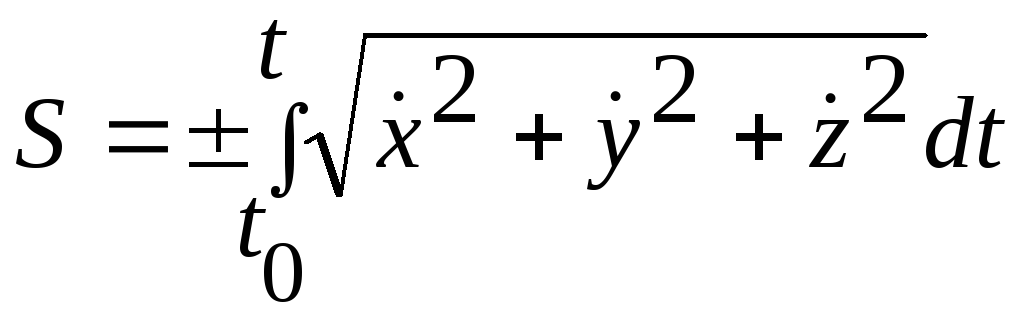(2.9)

Знак плюс соответствует движению в положительном направлении отсчета дуговой координаты, знак минус – положительному направлению. В формулах (2.8) и (2.9)

,,- производные по времени от соответствующих координат (см. формулы 2.13).

ОПРЕДЕЛЕНИЕ ТРАЕКТОРИИ ДВИЖЕНИЯ ТОЧКИ.

Пример №1.

Кривошип вращается с постоянной угловой скоростью. Найти траекторию движения средней точкишатуна, если. В начальный момент времени ползуннаходиться в крайнем правом положении. Начало координат поместить в точку.

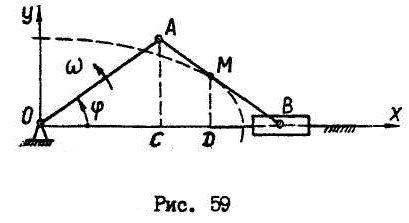
Положение механизма определяется углом поворота ведущего звена – кривошипа, изменяющимся во времени по закону.

В выбранной системе отсчета выразим координаты точки :

. (1)

С учетом исходных данных уравнения (1) примут вид:

. (2)

Уравнения (2) определяет закон движения точки . Для нахождения уравнения траектории из уравнений движения необходимо исключить параметр:

, .

Возведем в квадрате и сложим:

.

Следовательно, средняя точка шатуна движется по замкнутой эллиптической траектории с центром в точкеи полуосям:

, .