В) г)
Рисунок 33
Прямая параллельна плоскости.
Если прямая линия параллельна какой-либо прямой, находящейся в плоскости, то она параллельна этой плоскости. Следовательно, для построения прямой, параллельной заданной плоскости, надо взять в этой плоскости какую - либо прямую и построить ей параллельную.
|
На рис. 34 через точку С проведена прямая d, параллельная плоскости Р, заданной пере-секающимися прямыми m и n. Прямая d параллельна прямой n, принадлежащей плоскости P (m,n), следовательно, прямая d параллельна этой плоскости: (d1 n1; d2 n2) d P (m,n) |
Рисунок 34 |
Прямая перпендикулярна плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
|
Чтобы построить перпендикуляр из точки D на плоскость треугольника АВС (рис.35) необходимо предварительно построить горизонталь h (А-1) и фронталь плоскости f (В-2). Горизон-тальная проекция перпендикуляра пройдет через точку D1 перпендикулярно к горизонтальной проекции горизонтали А1-11 (h1), а фронтальная проекция — перпендикулярно к фронтальной проекции фронтали В2-22 (f 2). Если же плоскость задана следами, то, учитывая, что |
Рисунок 35 |
|
фронтальная проекция любой фронтали в этой плоскости всегда параллельна фрон-тальному следу плоскости, а горизонтальная проекция любой горизонтали параллельна горизонтальному следу плоскости, легко видеть (рис. 36), что проекции перпен-дикуляра к плоскости должны быть перпендикулярны соот-ветствующим следам плоскости.
Плоскости перпендикулярны Две плоскости взаимно перпендикулярны, если одна из них проходит через перпен-дикуляр к другой. На рис. 37 через прямую АВ проведена плоскость, перпендикулярная плоскости треугольника CDE. Для этого из точки В прямой А В восстановлен перпендикуляр (ВК) к плоскости треугольника CDE (В2К2 f2 и В1К1 h1, где f и h — фронталь и горизонталь плоскости треугольника CDE). |
Рисунок 36
Рисунок 37 |
Плоскость, определяемая пересекающимися прямыми АВ и ВК — искомая.
**Если возникает необходимость в построении взаимно перпендикулярных прямых общего положения, необходимо построить плоскость, перпендикулярную заданной прямой, и взять в ней любую прямую.
Задача.
Через точку М провести прямую, перпендикулярную прямой l.
Для построения взаимно перпендикулярных прямых (рис. 38), одна из которых l задана, а вторая (чтобы задача имела единственное решение) должна проходить через какую-либо определенную точку (М), надо выполнить следующее:
|
а) через заданную точку М проводим плоскость Q (h f), перпендикулярную заданной прямой l (h1 l1 f2 l2); б) находим точку пересечения заданной прямой l с построенной плоскостью Q — точку К (для этого прямую l заключаем во вспомогательную фронтально – проецирующую плоскость Р); в) соединяем заданную точку М с найденной точкой К прямой линией. Эта линия МК и будет искомой.
|
Рисунок 38
|
Задача.
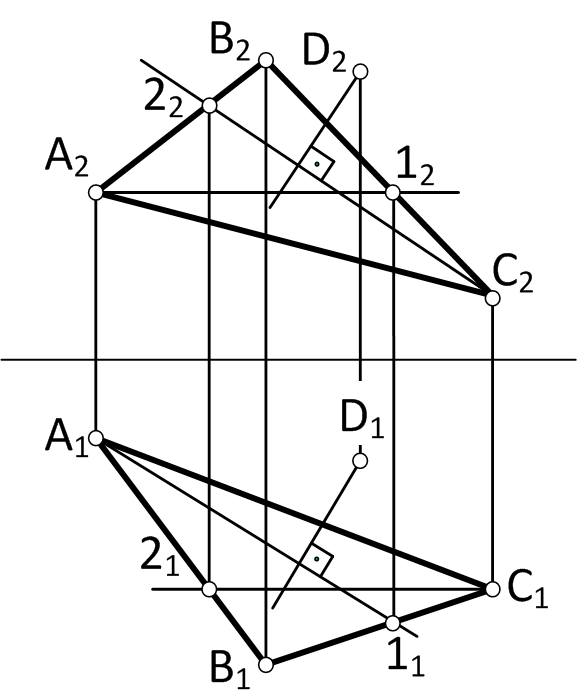
Определить расстояние от точки до плоскости, заданной треугольником АВС (рис. 39)
Расстояние от точки до плоскости определяется длиной перпендикуляра, опущенного из точки на плоскость. Поэтому решение этой задачи выполняем в следующей последовательности:
|
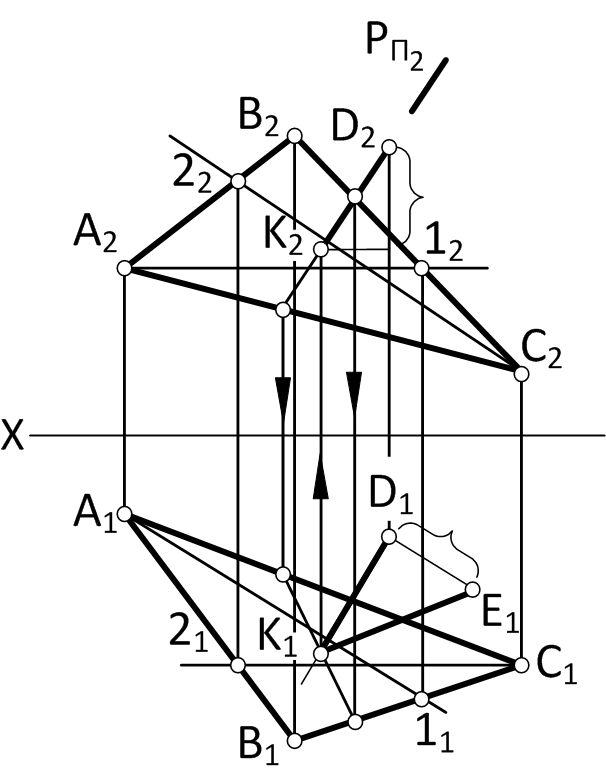
1. Из точки D (рис.39,а) опускаем перпендикуляр на плоскость треугольника АВС, для этого в плоскости треугольника проводим горизонталь (А212, А111) и фронталь (С222, С121); затем из точки D2 опускаем перпендикуляр на С222 – получаем фронтальную проекцию перпендикуляра; а из точки D1 – на А111 – получаем горизонтальную проекцию перпендикуляра к плоскости DАВС. 2. Находим точку пересечения перпендикуляра с плоскостью DАВС: заключаем перпендикуляр во вспомогательную секущую плоскость Р; строим линию пересечения плоскости DАВС с плоскостью Р; определяем искомую точку (К) в пересечении перпендикуляра и построенной линии пересечения 3-4(рис. 39б). 3. Методом прямоугольного треугольника определяем натуральную величину отрезка DK, для чего в плоскости 1 (рис. 39,в) строим прямоугольный треугольник один катет которого является горизонтальной проекций перпендикуляра, а второй равен разности высот точек D и K. Гипотенуза (К1Е1) построенного треугольника определяет искомое расстояние от точки D до плоскости треугольника АВС.
|
Рисунок 39,а
Рисунок 39,б
|
|
|
Рисунок 39,в
|