
- •Раздел 2 Программирование на языке
- •Лабораторная работа № 1
- •1 Порядок решения задач на компьютере
- •2 Разработка линейных программ
- •Input "Ввести d, k,n"; d, k,n
- •3 Операторы read, datа, restore
- •3 Запуск qbasic, ввод и редактирование программ
- •Лабораторная работа № 2
- •2 Программы ветвления
- •Input X
- •Лабораторная работа № 3
- •1 Операторы цикла qb
- •2 Примеры программ с циклами
- •3 Контрольные вопросы
- •4 Задание
- •Лабораторная работа № 4
- •1 Программа вычисления арифметического ряда
- •2 Программы вычисления факториалов
- •3 Алгоритм итерационного цикла
- •4 Контрольные вопросы
- •5 Задания
- •Лабораторная работа № 5
- •1 Программа "цикл в цикле"
- •2 Программа "цикл и ветвление"
- •3 Программа "цикл в цикле и ветвление"
- •4 Контрольные вопросы
- •5 Задания
- •Лабораторная работа № 6
- •1 Одномерные массивы - векторы
- •2 Двумерные массивы – матрицы. Обработка массивов
- •3 Контрольные вопросы
- •4 Задания
- •Лабораторная работа № 7
- •1 Функции пользователя
- •3 Процедуры. Операторы sub и end sub
- •Лабораторная работа № 8
- •1 Графические операторы qbasic
- •2 Программа рисования графических объектов
- •3 Построение графиков функций
- •4 Контрольные вопросы
- •5 Задание
5 Задания
|
№ варианта |
Выражение |
|
1 |
2 |
|
1 |
t z = t -│20-t , если 4<t<=9.8 |
|
2 |
( S = cos x+e sin x , если 0.2<x<=1 |
|
3 |
z y = 3 sin(z-0.4)-z , если 0.4<=z<=2.5 |
|
4 |
( y = x 12+x , если 11<x<=17 |
|
5 |
3 z = tg x + cos y , если 2<=y<=4 |
89
|
1 |
2 |
|
6 |
y = cos z , если 0<=z<=1 |
|
7 |
z = 2√t ,если 0<=t<=2 |
|
8 |
z = 1-xy 0.5<=y<=0.8 |
|
9 |
C = |z-6| , если 3<=z<=8 |
|
10 |
y = (t-(t-3)) , если 0<=t<=4 |
|
11 |
M = │cos x│x-2 ,если 0<x<=10 |
|
12 |
z = 5ax , 0.5<=a<=2.5 |
|
13 |
z = (S-cos S) , если 0<S<=1.5 |
|
14 |
y = sin(a+x) -1<=a<=1 |
|
15 |
S = (y sin y-1) , если 1<y<=4 |
|
16 |
y = ax , 0.1<=a<=0.2 |
|
17 |
y = cos z 0.1<=z<=2.5 |
|
18 |
y = b cos x , если 1<x<2 |
|
19 |
y = sin(bx+a) , если 1<x<=2 |
|
20 |
y = x+sin x-cos x, если 0.9<x<=1 |
Содержание отчета
1 Название,цель, содержание работы
2 Задание для своего варианта.
3 Схема алгоритма.
4 Программы.
5 Результаты расчётов в среде QB.
6 Письменные ответы на контрольные вопросы.
7 Выводы по работе
90
Лабораторная работа № 6
Обработка массивов
Цель работы: разработка программ, реализующих вычислительные
процессы.с индексированными переменными
Содержание работы:
1 Одномерные массивы - векторы
2 Двумерные массивы - матрицы". Обработка массивов
Индексированные переменные
Ранее при составлении программ использовались простые переменные, которые имели свое имя и обращение к ним осуществлялось по этому имени. Под каждую из простой переменной автоматически выделяется ячейка памяти. Многие важные задачи трудно или невозможно решить с использованием только простых переменных. В подобных случаях целесообразно использовать массивы.
Массивом называется упорядоченная последовательность вели-
чин, обозначаемая одним именем. Допуск к конкретному элементу
этой последовательности осуществляется по его порядковому номеру (индексу), который указывается рядом с именем массива в квадратных скобках. Массивы иначе называются индексированными переменными.
Примеры: A[2], В[5,10], D[I] означает второй элемент массива А, элемент пятой строки десятого столбца массива В и i-й элемент массива D. Такая запись обусловлена тем, что в языках программирования индексы и показатели степени не используются, а все выражения записываются в одну строку.
Массивы по способу организации делятся на одномерные – массивы-векторы (напр., A[1], В[10], D[I]) и двумерные – массивы-матрицы (напр., Е[3,3], T[5,8], G[I,J])
Примечание. На самом деле в QBASIC нумерация элементов массива начинается с 0, а не с 1, т.е. А[3] указывает на 4-й элемент массива-вектора А, а M[3,5] – на элемент 4-й строки 6-го столбца массива-матрицы М. Но человеку удобнее считать не с 0 до 9, а с 1 до 10, поэтому обычно 0-й элемент массива не используется в расчётах (или используется редко), хотя память под него в QBASIC резервируется.
В качестве номера элемента индексной переменной может использоваться арифметическое выражение, в этом случае после вычисления ее значения дробная часть отбрасывается.
91
Пример. После вычисления индексного выражения C[5.2,Y+I^2]
при Y=3,2 и I=5 будет определен элемент С[5,28].
Элементы массива могут употребляться в программе так же, как и простые переменные, но под массивы компьютер должен выделять память заранее. Если под простую переменную выделяется одна ячейка памяти в тот момент, когда переменная впервые встретится в программе, то при работе с массивами первому использованию переменной с индексом должно предшествовать описание, сообщающее какие массивы используются в программе и каков размер каждого массива.
Эта информация задается в операторе описания массивов DIM, в котором указывается имя массива и, в квадратных скобках, верхние границы изменения индексов. Индексы должны быть целыми положительными числами.
Пример. DIM A[3], B[4,5], T$[12] описывает три массива: массив А, состоящий из четырех элементов: А[0], А[1], А[2], А[3]; массив В, содержащий 5 строк и 6 столбцов и T - символьный массив, содержащий 13 нечисловых элементов.
В QBASIC может быть объявлен массив с произвольной размерностью, в котором границы изменения индексов задаются с помощью переменных. Эти переменные в программе обычно определяются оператором INPUT.
Например.
INPUT E,F
DIM B[E,F]
Оператор DIM B[E,F] описывает массив В, размер которого определяется после ввода переменных E и F в процессе выполнения программы.
Основным инструментом при обработке массивов данных являются циклы.
Общие принципы программирования циклов сохраняются, но в качестве управляющих переменных цикла выступают переменные, определяющие
значения индексов.

 (8-7(-t))
, если -1.4<=t<=4
(8-7(-t))
, если -1.4<=t<=4 2-x)+│x│
,если
-0.8<=x<=0.2
2-x)+│x│
,если
-0.8<=x<=0.2 (4-z)
, если -2.5<=z<0.4
(4-z)
, если -2.5<=z<0.4 12-x)x
, если 5<=x<=11
12-x)x
, если 5<=x<=11 .14+xy
, если 1<=x<=10
.14+xy
, если 1<=x<=10 sin
(x
+1) , если 0.1<=x<=0.5
sin
(x
+1) , если 0.1<=x<=0.5
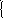 е2е
+ esin
t
, если
-1.5<=t<0
е2е
+ esin
t
, если
-1.5<=t<0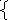 x+y
0.1<=x<=0.3
x+y
0.1<=x<=0.3  (z-1)
, если 0<=z<=3
(z-1)
, если 0<=z<=3 t+4sin
t│ ,если
-2<=t<0
t+4sin
t│ ,если
-2<=t<0 x-1
– lnx4
, если -5<=x<=0
x-1
– lnx4
, если -5<=x<=0 2+3(a-x)
, 0.1<=x<=17.55
2+3(a-x)
, 0.1<=x<=17.55 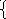 (S
-2S-2) , если
-2<=s<=0
(S
-2S-2) , если
-2<=s<=0 a+sin
x -2<=x<=7
a+sin
x -2<=x<=7  (cos(y-1)-2)
, ,если
-3<=y<=1
(cos(y-1)-2)
, ,если
-3<=y<=1 sin│x/a│
, 0.5<=x<=3.5
sin│x/a│
, 0.5<=x<=3.5  b
sin x 0<=x<=2
b
sin x 0<=x<=2  a
sin x , если
0.1<=x<=1
a
sin x , если
0.1<=x<=1  │ax
+bx │, если
0.1<=x<=1
│ax
+bx │, если
0.1<=x<=1  cos
x , если
0.5<x<=0.9
cos
x , если
0.5<x<=0.9