2.5. Проверка прочности по нормальным напряжениям в верхнем поясе

По нормальным напряжениям в верхнем поясе

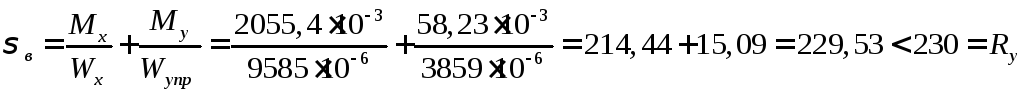
Проверка по нормальным напряжениям в нижнем поясе

Проверка по касательным напряжениям

.

Проверка по напряжениям местного смятия стенки от давления кранового колеса

.

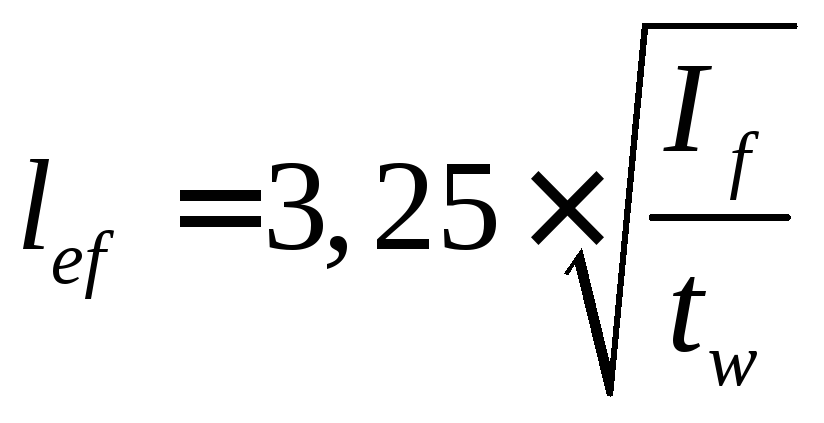, где

Проверки показывают, что прочность принятого сечения обеспечена.

2.6. Проверка жесткости и устойчивости

Проверка жесткости необходима, если в нашем случае 1200 < 1250.

Определим прогиб балки

Жесткость подобранного сечения обеспечена.

Общая устойчивость подкрановой балки обеспечена тормозной конструкцией и не проверяется

2.7. Проверка местной устойчивости стенки подкрановой балки

Определяем условную гибкость стенки

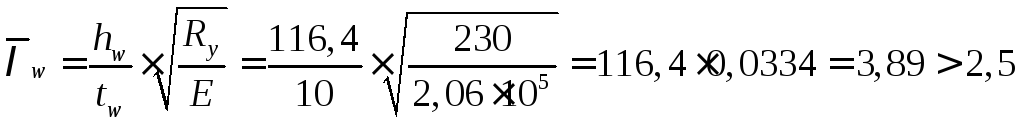т.е. устойчивость стенки нужно проверять.

При следует устанавливать основные поперечные ребра жесткости. Расстояние между ними, если. При. Принимаем(кратно пролету). Размеры отсека стенки(см. рис. 2.6).

Принимаем подкрановую балку с двусторонними поясными швами и двусторонними основными поперечными ребрами жесткости.

Ширина ребра должна быть не менееи не менее.

.

Принимаем .

Толщина ребра .

2.7.1. Проверяем устойчивость среднего отсека

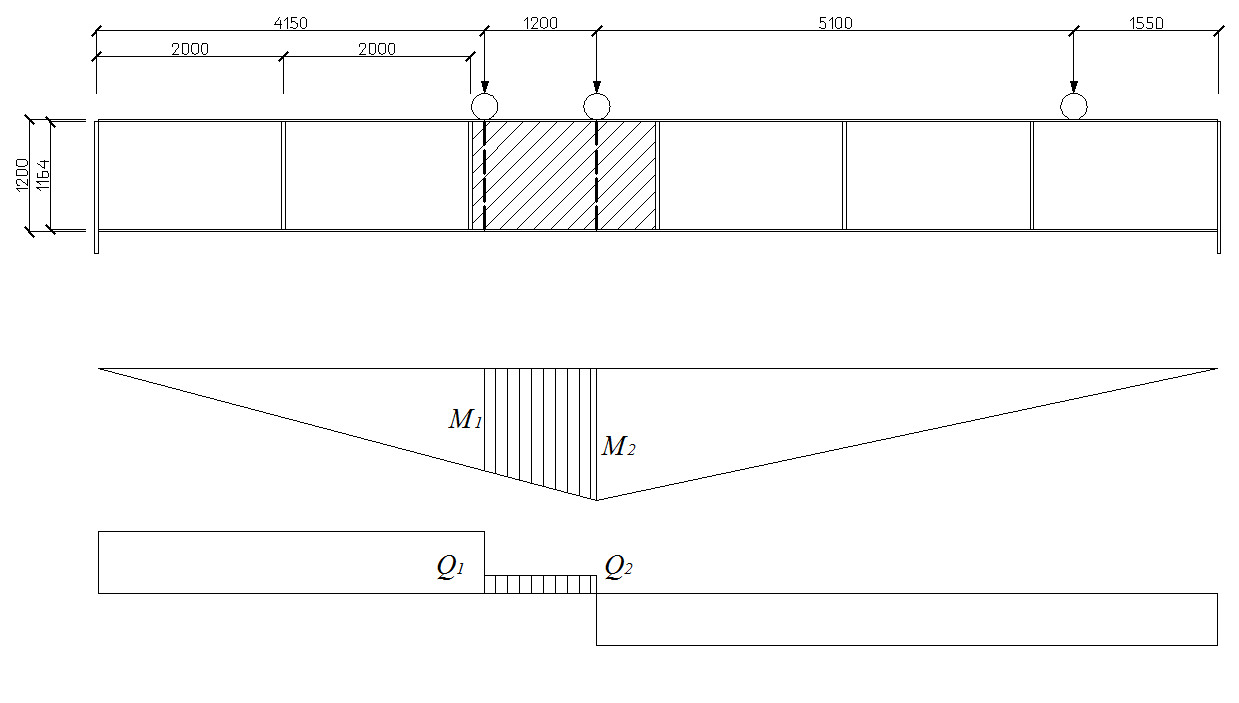
Рис. 2.5

Напряжения в среднем отсеке определяются при загружении по схеме определения .

Определяем усилия для наиболее напряженного участка отсека.

Опорные реакции

Изгибающие моменты

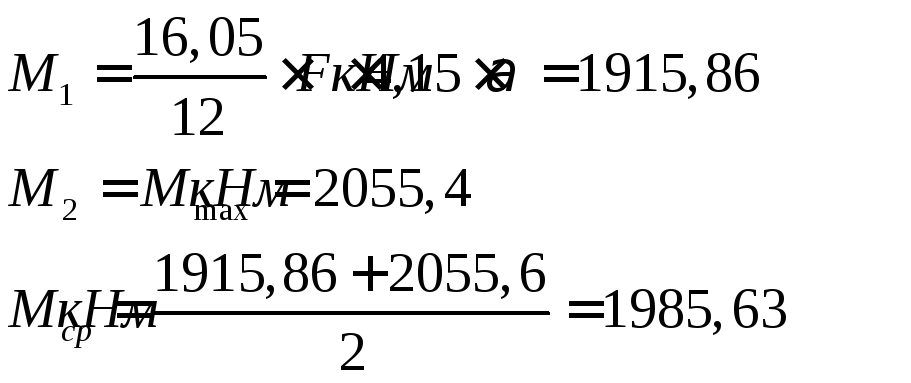
Поперечные силы

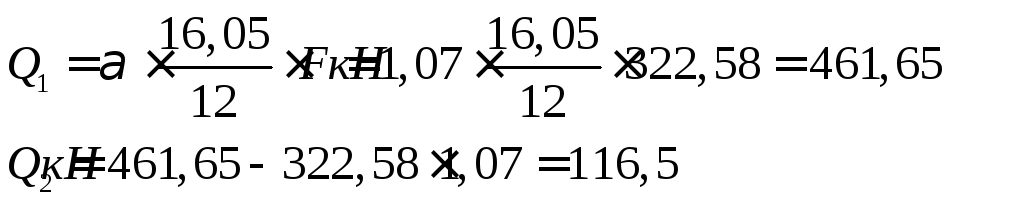
Определяем напряжения

(из проверки прочности)

Определяем критические напряжения для отсека .

Соотношение размеров отсека

.

Соотношение .

Коэффициент защемления стенки

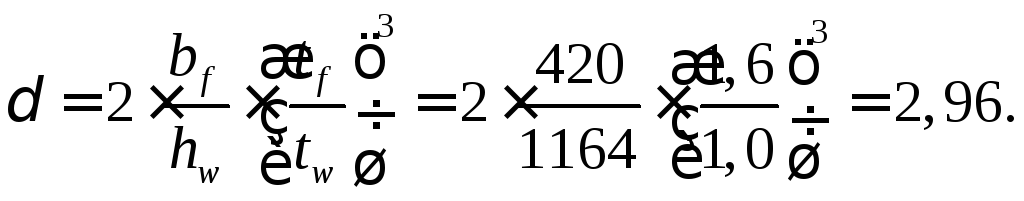
При ипотабл. 1.3

определяются по формулам (36):

, где

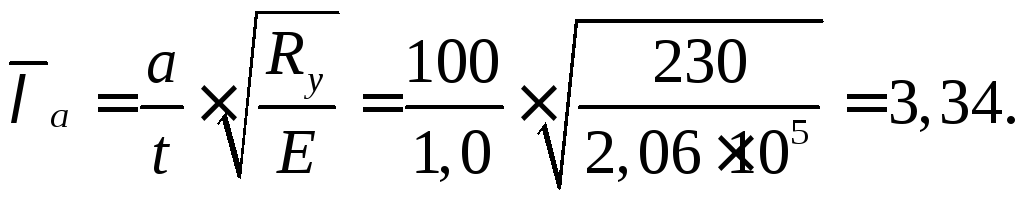
см. табл. 1.4 [4], при.

, где

,

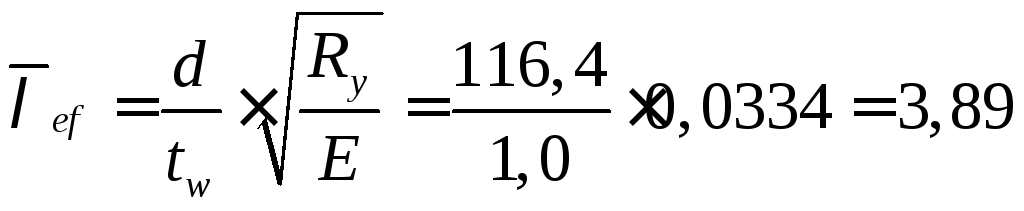,- меньшая сторона отсека.

Устойчивость стенки балки проверяется по формуле (28):

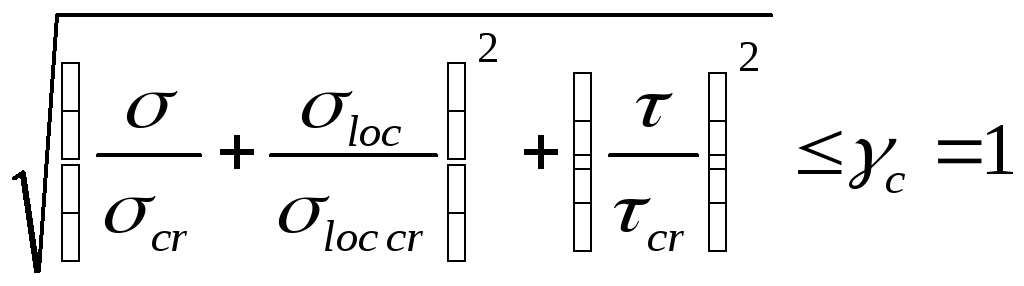
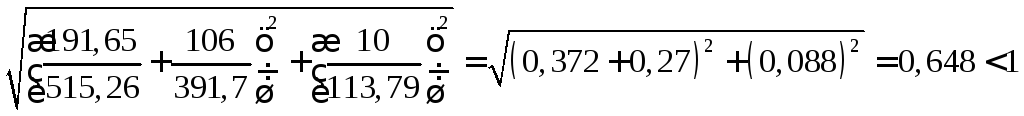
Устойчивость стенки при обеспечена.

Проверяем устойчивость крайнего отсека при загружении по схеме на рис 2.7.

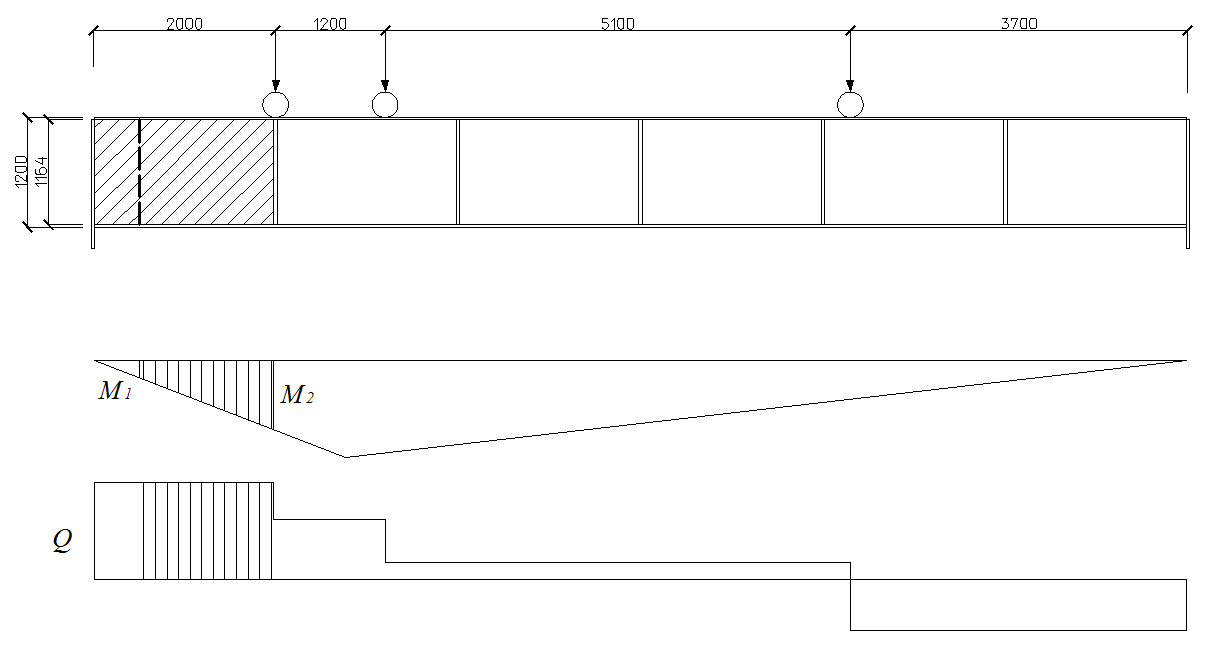
Рис. 2.6

Определяем усилия для наиболее напряженного участка отсека длиной .

Опорная реакция при схеме загружения (см. рис. 2.7)

Изгибающие моменты

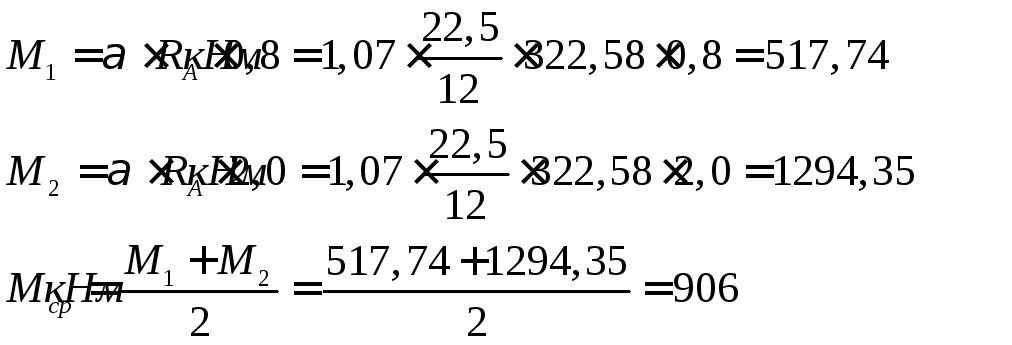
Поперечная сила

Определяем напряжения

Проверяем устойчивость стенки в крайнем отсеке.

Критические напряжения для крайнего отсека равны - для среднего, т.к. размеры их одинаковы.

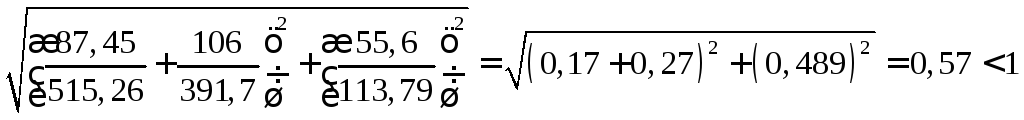
Следовательно толщина стенки и размещение ребер черезобеспечивают устойчивость стенки.

2.8. Расчет опорного ребра

Для передачи опорного давления балки на колонну предусматриваем торцевую диафрагму с пристроганным нижним краем, называемую обычно опорным ребром.

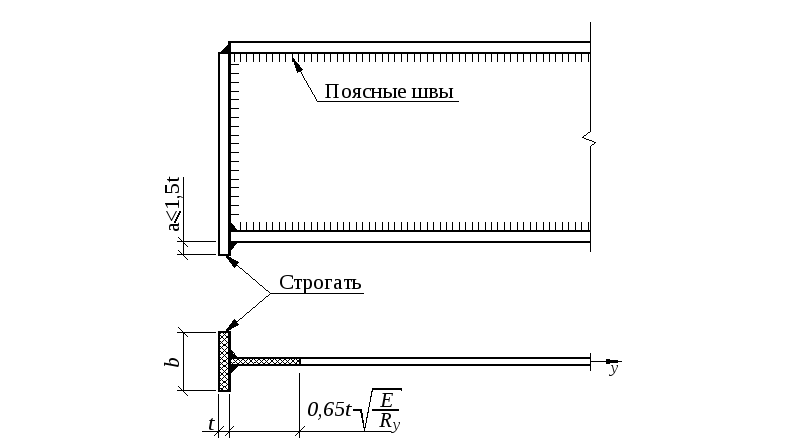
Рис. 2.7.– К расчету опорного ребра

Площадь строганного края опорного ребра определяется из условия прочности его на смятие, если

- расчетное сопротивление стали смятию.

По конструктивным требованиям ;.

Принимаем ;;.

Проверяем устойчивость опорной части из плоскости балки (относительно оси ), как стойки с шарнирно опертыми концами высотой.

В сечение опорной части включается

.

Момент инерции опорной части

Радиус инерции

.

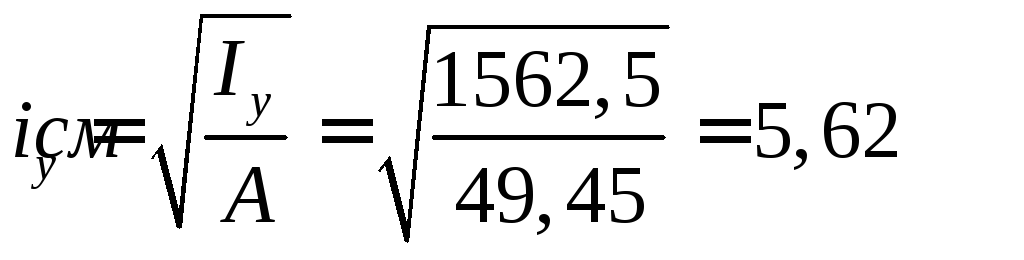поопределяем;

Проверяем устойчивость опорной части балки по формуле

Устойчивость опорной части балки обеспечена.