5.3 Плоскопараллельное движения твердого тела (задача к 2)

5.3.1 Порядок решения задач при определении

кинематических параметров плоского движения твердого тела

Решение задач на плоское движение твердого тела рекомендуется выполнять в следующей последовательности:

• изобразить механизм в заданном положении, соблюдая заданные углы и размеры звеньев;

• установить виды движений звеньев механизма;

• определить скорость точки ведущего звена механизма;

• найти положения МЦС звеньев, совершающих плоское движение;

• определить расстояния от МЦС до точек механизма, скорости которых необходимо рассчитать по условию задачи, и вычислить эти скорости из соответствующих пропорций;

• проверить найденные скорости точек механизма, используя теорему о проекциях скоростей двух точек на прямую, соединяющую эти точки;

• используя метод полюса, найти ускорения точек А и В механизма и угловую ускорение звена АВ;

5.3.2 Условие задачи к 2

Плоский механизм (рисунки 15, 16, 17, 18) состоит из трех или четырех стержней и одного или двух ползунов.

Для всех вариантов принять:

- угловая скорость кривошипа О₁А: ₁ = 2, 0 с^-1;

- длина стержней механизма:

₁ = 0,4 м; ₂ = 1,5 м; ₃ = 1,2 м; ₄= 0,6 м; АС = ВС.

В соответствии с заданными кинематическими параметрами ведущего звена механизма определить:

1. скорости указанных на рисунке точек и угловые скорости звеньев методом МЦС;

2. проверить найденные скорости точек, используя теорему о проекциях скоростей двух точек на прямую их соединяющую;

3. ускорения точек А и В механизма и угловое ускорение звена 2 методом полюса.

5.3.3 Пример решения задачи к 2

Исходные данные к расчету :

Угловая скорость кривошипа .

Длины стержней : .

Определить кинематические параметры движения точек и звеньев механизма в соответствии с условием задачи.

Решение

Изобразим механизм в заданном положении, соблюдая заданные углы и размеры звеньев (рисунок 12). Механизм рекомендуется изобразить в масштабе М 1:10.

1

60⁰

А

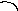
60⁰

4

О1

B

120⁰

D

2

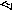
Е

О3

60⁰

3

Рисунок 12

Определяем скорости точек и угловые скорости звеньев механизма.

Звено совершает вращательное движение. Зная угловую скоростьзвена, определим скорость точки А:. Векторнаправлен перпендикулярно звену 1 в сторону его вращения.

Звено АЕ совершает плоскопараллельное движение. Точка Е принадлежит одновременно этому звену, совершающему плоскопараллельное движение и звену ЕО₂, вращающемуся вокруг оси, проходящей через точку . Так как направление скоростейидвух точек звена 2 известны, то мгновенный центр скоростей (МЦC) звена – точка находится на пересечении перпендикуляров проведенных к векторам скоростейи. Скорости точек пропорциональны их расстояниям до МЦС и связаны соотношением

. (5)

Так как - равносторонний, то, и тогда

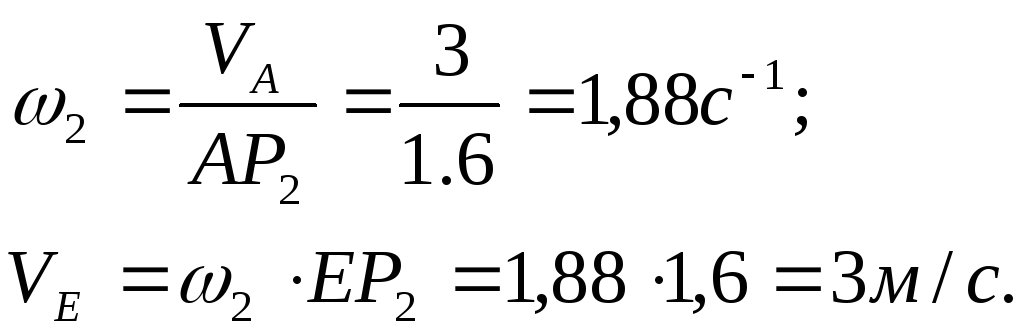
Направление угловой скорости определим по направлению вектораскорости точки А. ТочкаD так же принадлежит звену 2. Вектор скорости точкиD направлен перпендикулярно отрезку DP₂ в сторону, соответствующую направлению угловой скорости (рисунок 13).

В отрезокDP₂ является высотой :

.

Тогда .

Вектор скорости точкиD направлен перпендикулярно отрезку DP₂ в сторону, соответствующую направлению угловой скорости звена 2.

Скорость точки Е звена 2 можно определить, используя теорему о проекциях скоростей двух точек. Проекции скоростей двух точек на прямую, их соединяющую (на прямую АЕ), равны между собой:

.

Откуда ==3м/с.

Угловую скорость звена 3, вращающегося вокруг неподвижной оси , определим по известной скорости точки Е:

.

Звено АЕ совершает плоскопараллельное движения. Скорость точки D известна по модулю и направлению. Ползун В движется в горизонтальных направляющих, следовательно , направление вектора скорости точки В известно. МЦС звена 4 – точканаходится на пересечении перпендикуляров, проведенных к векторами. Скорости точек Д и В связаны соотношением

. (6)

Из находим;

.

Тогда .

Направление угловой скорости определяем по направлению вектора скорости:.

Скорость точки В найдем по теореме о проекциях скоростей точки D и В на прямую ВD: ;

.

Теперь определим ускорение точек А и Е и угловое ускорения звена АЕ. Звено равномерно вращается вокруг оси, поэтому ускорение точки А будет представлено только его нормальной составляющей

.

1

Е

3

2

А

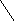
Рисунок 13

Так как точка Е принадлежит вращающемуся звену 3, ускорение точки Е будет представлено двумя составляющими :

, (8)

где ;

.

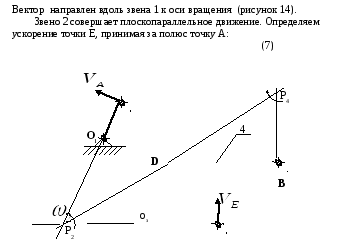
Вектор направлен вдоль звена 3 к оси вращения. Вектор направлен перпендикулярно нормальной составляющей ускорения (рисунок 14).

Ускорение во вращательной составляющей плоского движения так же представлено двумя составляющими :

, (9)

где

B

D

О₃

60⁰

60⁰

120⁰

1

4

2

А

О₁

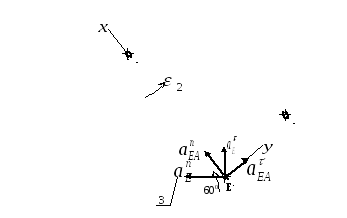
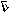
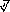
Рисунок 14

Вектор направлен от точки Е к полюсу – точке А. Векторнаправлен перпендикулярно нормально составляющей. С учетом уравнений (8) и (9) равенство (7) примет вид :

. (10)

В векторном равенстве (10) ускорение и известны только по направлению, остальные векторы определены по модулю и по направлению. Для нахождения неизвестных величин спроецируем равенство (6) на две взаимно перпендикулярные оси Х и Y, направляя ось Х вдоль звена АЕ.

На ось Х : .

Откуда

.

Знак минус показывает, что действительное направление вектора противоположно принятому первоначально.

На ось Y :

.

Откуда

Угловое ускорение звена АЕ :.

Направление углового ускорения определяем по направлению вектора.

Полное ускорение точки Е найдем по формуле

.