
- •IIчасть
- •Тема 1.Первообразная. Неопределенный интеграл, его свойства. Таблица основных интегралов. Непосредственное интегрирование. Интегрирование по частям и подстановкой.
- •1 Интегральное исчисление
- •1.1 Первообразная, неопределенный интеграл
- •2 Методы интегрирования
- •2.1 Метод подведения под знак дифференциала (устная замена переменной)
- •2.2 Метод письменной замены переменной (подстановки)
- •2.3 Метод интегрирования по частям
- •3 Определенный интеграл
- •3.1 Задача о площади.
- •3.2 Понятие определенного интеграла
- •3.3 Свойства определенного интеграла
- •4.3 Ду с разделяющимися переменными
- •4.4 Однородные функции
- •4.5 Однородные дифференциальные уравнения первого порядка
- •4.6 Линейные дифференциальные уравнения первого порядка
- •4.7 Линейные однородные д.У. Второго порядка с постоянными коэффициентами
- •4.8 Линейные неоднородные ду второго порядка с постоянными коэффициентами и специальной правой частью.
- •4.9 Системы дифференциальных уравнений
- •5.4 Знакопеременные ряды
- •5.5 Степенные ряды
- •6. Теория вероятностей
- •6.1 События. Операции над событиями
- •6.2 Вероятность события
- •6.3 Элементы комбинаторики
- •6.4 Основные теоремы.
- •6.5 Случайные величины
- •5.6 Числовые характеристики
- •Iiчасть
- •350072, Краснодар, ул. Московская, 2-а
4.4 Однородные функции
Функция f(x,y) называется однороднойk-ой степени однородности, если выполняется равенство:
![]() .
.
В частности, если
![]() – функция однородная нулевой степени
однородности.
– функция однородная нулевой степени
однородности.
Примеры
1)
![]() .
.
![]() – однородная функция второй степени
однородности.
– однородная функция второй степени
однородности.
2)
![]() .
.
 – однородная функция нулевой степени
однородности.
– однородная функция нулевой степени
однородности.
4.5 Однородные дифференциальные уравнения первого порядка
ДУ первого порядка называется однородным,
если его можно представить в виде
![]() ,
где
,
где![]() – однородная функция нулевой степени
однородности. Однородное уравнение
сводится к уравнению с разделяющимися
переменными с помощью подстановкиy=xt,
dy=xdt+tdx.
– однородная функция нулевой степени
однородности. Однородное уравнение
сводится к уравнению с разделяющимися
переменными с помощью подстановкиy=xt,
dy=xdt+tdx.
Примеры
1)
![]() ;
;
![]()
xdy=(x+y)dx, y=xt, dy=xdt+tdx
x(xdt+tdx)=(x+xt)dx
xdt+tdx=(1+t)dx
xdt+tdx=dx+tdx
xdt=dx
![]()
![]()
![]() ,
вернемся к старой переменной
,
вернемся к старой переменной
![]()
![]() .
.
2)
![]()
![]()
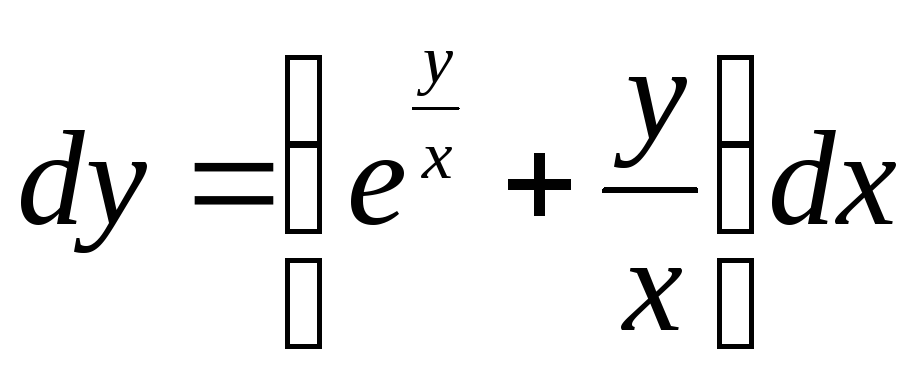
Пусть y=xt, dy=xdt+tdx,
![]()
![]()
![]()
![]()
![]() ;
;
-е-t=ln|x|+C.
Вернемся к старым переменным:
![]() .
.
4.6 Линейные дифференциальные уравнения первого порядка
ДУ первого порядка называется линейным,
если его можно представить в виде
![]() ,
гдеP(x),Q(x)– заданные функции (функция y
и ее производная или дифференциалdy
входят в уравнение линейно, т.е. в
первой степени и порознь друг от друга).
,
гдеP(x),Q(x)– заданные функции (функция y
и ее производная или дифференциалdy
входят в уравнение линейно, т.е. в
первой степени и порознь друг от друга).
Один из способов решения – метод Бернулли (подстановка Бернулли).
Будем искать решение в виде y=UV,
тогда![]() Подставим в уравнение
Подставим в уравнение![]()
![]() .ВыберемVтак, чтобы
.ВыберемVтак, чтобы![]() ,
тогда
,
тогда![]() .
.
Таким образом, решение данного линейного уравнения сводится к последовательному решению двух уравнений с разделяющимися переменными:
![]() ,
решая его находимV,
подставляемVво
второе:
,
решая его находимV,
подставляемVво
второе:
![]() ,
из которого находимU.
,
из которого находимU.
Тогда решение первоначального уравнения
имеет вид
![]()
Примеры(см. задание 4):
1)
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
,
![]() ,
сведем его к двум уравнениям
,
сведем его к двум уравнениям
1)
![]() ;
;
2)
![]() ,
решаем их последовательно.
,
решаем их последовательно.
а)
![]()
![]()
![]()
![]()
![]()
![]() (ищем частный интеграл)
(ищем частный интеграл)
V = cos x.
б)
![]()
![]()
![]()
![]()
![]()
U = sin x + C,
Тогда решение первоначального уравнения имеет вид
![]() .
.
2)
![]() ,
,![]() при
при![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
|
а)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б)
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() – общее решение. Выделим частное решение,
удовлетворяющее начальным условиям:
– общее решение. Выделим частное решение,
удовлетворяющее начальным условиям:![]() ;
;![]() ;
;
![]()
4.7 Линейные однородные д.У. Второго порядка с постоянными коэффициентами
Это уравнения вида
|
|
(1) |
где
![]() – константы.
– константы.
Общее решение такого уравнения имеет вид
![]()
где
![]() – произвольные постоянные
– произвольные постоянные
![]() -общее
решение однородного уравнения,
-общее
решение однородного уравнения,
![]() -линейно
независимые частные решения уравнения
(1).
-линейно
независимые частные решения уравнения
(1).
Определение. Функции![]() и
и![]() называются линейно независимыми
(зависимыми) на (a,
b), если при
называются линейно независимыми
(зависимыми) на (a,
b), если при![]()
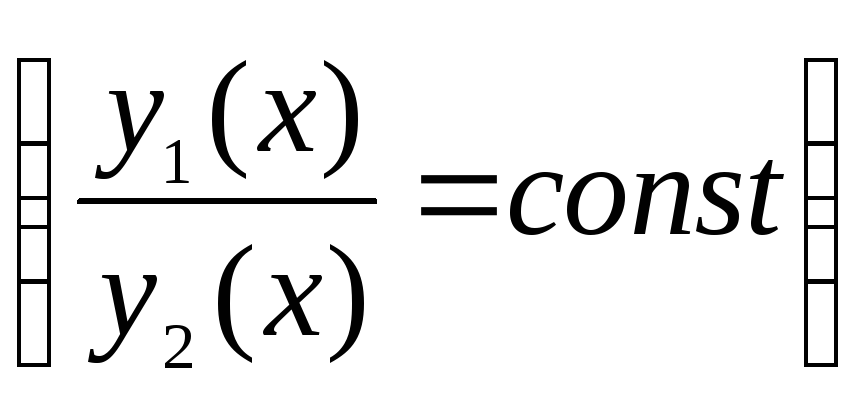
Решение уравнения (1) сводится к решению алгебраического уравнения
|
|
(2) |
называемого характеристическим, в котором степень kравна порядку производной в уравнении (1).
При этом возможны следующие случаи:
1. При
![]() уравнение (2) имеет действительные
различные корни
уравнение (2) имеет действительные
различные корни![]() ,
тогда частные решения ДУ (1) имеют вид
,
тогда частные решения ДУ (1) имеют вид![]() ,
,![]() (в чем можно убедится непосредственной
подстановкой).
(в чем можно убедится непосредственной
подстановкой).
Они линейно независимы (смотри определение). Тогда общее решение (1) имеет вид:
![]()
2. При
![]() характеристическое уравнение (2) имеет
два действительных равных корня
характеристическое уравнение (2) имеет
два действительных равных корня![]() ,
тогда частными решениями Д.У. (1) являются
функции
,
тогда частными решениями Д.У. (1) являются
функции![]() ,
общее решение (1) имеет вид
,
общее решение (1) имеет вид
![]()
3. Если
![]() ,
то характеристическое уравнение (2) не
имеет действительных корней, но имеет
комплексные корни вида
,
то характеристическое уравнение (2) не
имеет действительных корней, но имеет
комплексные корни вида![]() .
.
Тогда частные решения
![]()
Общее решение (1) имеет вид
![]()
Примеры(см. задание 5):
1)
![]() ,
составим характеристическое уравнение:
,
составим характеристическое уравнение:![]()
![]() ;
;![]() ;
;![]() .
.
![]()
2)
![]() ,
составим характеристическое уравнение
,
составим характеристическое уравнение![]()
![]() ;
;
![]() ;
;
![]() .
.
3)
![]()
![]()
![]()
![]()
4)
![]()
![]()
![]()
![]()
