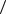Yang Fluidization, Solids Handling, and Processing

Attrition in Fluidized Beds and Pneumatic Conveying Lines 465

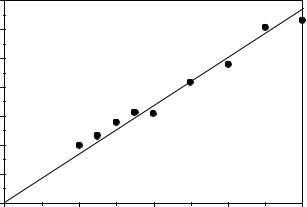
Figure 11. Variation of the steady-state attrition rate of coal ash (0.2 to 0.315 mm) with (Ug - Ug,mf ). (Pis et al., 1991.)

Figure 12. Variation of the steady-state attrition rate of limestone fractions with (Ug - Ug,mf ). (Ray et al., 1987a.)

466 Fluidization, Solids Handling, and Processing

Figure 13. Variation of the steady-state attrition rate of a catalyst with superficial gas velocity (AVN 802, Ug,mf = 0.002 m/s. (Xi, 1993.)

Bed Height. The effect of the bed height or bed weight on the bubbleinduced attrition rate Ra,bub is not quite clear. Merrick and Highley (1974)

and Pis et al. (1991) have found Ra,bub to be independent of bed height in accordance with Eq. (15). Kono (1981) found the attrition rate to be proportional to the static bed height with the exponent 0.78, Ra,bub H stat0.78 .

Furthermore, Ulerich et al. (1980) and Xi (1993) found Ra,bub to be proportional to the bed height. As an example Fig. 14 shows Xi’s results.

Obviously the role of bed height is not yet fully understood. Ray et al. (1987a) have explained these discrepancies by a consideration of bubble growth with height above the distributor. They argue that as long as the bubble size increases with height, the efficiency of the transformation of kinetic energy to free surface energy might increase thus leading to a bubbleinduced attrition rate that increases with bed height. However, as the bed height reaches the limits of slugging in small diameter columns or maximum attainable bubble in a large diameter bed, an extra bed height will not vary the conditions of bubbling and thus will result in Ra,bub becoming independent of bed height. However, further experiments are certainly needed in this area.

Attrition in Fluidized Beds and Pneumatic Conveying Lines 467

Figure 14. Variation of the steady-state attrition rate of a catalyst with bed height. (Xi, 1993.)

Internals. Commercial fluidized beds are often equipped with internals, e.g., baffle plates and heat exchanger tubes. Due to their interaction with the rising bubbles they will certainly cause particle attrition. Unfortunately, no systematic investigations are available in the open literature which could serve as practical guidelines.

Cyclones as Attrition Sources. Attrition in cyclones is a difficult field. The number of publications available in the open literature is very small. This may be due to the fact that experiences with the performance of cyclones are often considered proprietary. However, this lack of information can also be explained by strong experimental difficulties which mainly originate from the problem of making a distinction between the collection efficiency and attrition. The cyclone is a separator which is usually designed to keep as much material as possible inside the fluidized bed system. The material which cannot be kept inside the system, i.e., the loss or elutriation, is usually defined as attrition. But in fact, the elutriation rate originates from both sifted original fines entering the cyclone (i.e., from the original feed particle size distribution or produced by attrition in other parts of the fluidized bed system) and fines that are actually produced by attrition in the cyclone. Unfortunately, the attrition rates in other parts of the system and, therefore, their contribution to the elutriation rate is usually unknown.

468 Fluidization, Solids Handling, and Processing

Consequently, it is very difficult to evaluate the cyclone attrition rate from the measured elutriation rate. In order to study the cyclone attrition mechanism in detail it is necessary to study the cyclone in isolation. This can be achieved by feeding a cyclone batch-wise and directly without any additional equipment that could contribute to attrition.

Moreover, not all attrition products will be directly elutriated from the cyclone. Instead, a part will be collected by strands of the material and will be transported via the solids return line into the fluidized bed process. In subsequent passes through the cyclone, the accumulated attrition-produced fines will be elutriated due to the sifting effect of the cyclone.

For the special case of an isolated cyclone, which is fed with a mass

flux mc,in of material sufficiently large to be sent into the catch of the cyclone, the measured mass flux in the loss of the cyclone, mc,loss is solely due to attrition inside the cyclone. In such a case the cyclone attrition rate

Ra,c may be defined by

Modeling of Cyclone Attrition. A very simple model of cyclone attrition may be formulated in analogy to the models discussed with respect to jet attrition and bubble-induced attrition (Reppenhagen and Werther, 1997).

In the spiral or tangential cyclone inlet duct, the particles are accelerated to a velocity which is related to the inlet gas velocity Ue. Neglecting as a first approximation the slip between solids and gas, the kinetic energy of the solids which is transported per unit time into the cyclone is approximately given by

12 ×mc,in ×U e2

The fraction η of this kinetic energy is used to create free surface energy via abrasion,

where Sm is the mass specific surface area generated by abrasion and γ(J/m2) is the specific free surface energy of the solid material. Since abrasion produces very fine particles with a size distribution that is fairly

470 Fluidization, Solids Handling, and Processing

loss are not mixed again. Figure 17 gives an example of the results. The cyclone loss rate per single pass is plotted against the number of passes for given operating conditions (Ue, μ). In analogy to Fig. 2, a large initial cyclone loss rate is observed which rapidly decreases, and after 10 to 20 passes, reaches a steady-state value. The high value of the loss rate during the first couple of passes is due to the added effects of attrition and sifting, whereas the steady-state value is identical to the true cyclone attrition rate Ra,c. After thirty-four passes, the operating conditions were changed to a higher inlet velocity which, due to a constant solids feeding rate, was combined with a corresponding reduction in the solids loading. The measurements show a slow increase of the cyclone loss rate which, after another fifteen passes, leads to a steady state again. This slow transition is caused by the fact that part of the fines generated by attrition are sent into the catch of the cyclone.

According to the model described above the cyclone attrition rates Ra,c obtained under steady-state conditions have been plotted against the square of the cyclone inlet velocity in Fig 18. Although the number of experiments is not large the general relationship between Ra,c and Ue predicted by Eq. (19) is confirmed.

Figure 15. Changes in the size distribution of FCC catalyst due to attrition in a 5" cyclone, (inlet velocity 35ft/s). (Zenz and Kelleher, 1980.)

Attrition in Fluidized Beds and Pneumatic Conveying Lines 471

Figure 16. Experimental set-up for the isolated investigation of cyclone attrition (cyclone ID = 0.09 m). (By Reppenhagen and Werther, 1997.)

Figure 17. Cyclone loss rate of spent FCC catalyst as a function of the number of passes through the cyclone. (Reppenhagen and Werther, 1997.)

472 Fluidization, Solids Handling, and Processing

Figure 18. Influence of inlet velocity Ue and solids loading µ on the steady-state cyclone attrition rate. (Reppenhagen and Werther, 1997.)

As is seen from this latter figure, an increase of the solids loading results in a decrease in the cyclone attrition rate. This may be due to a “cushioning” effect of the increased solids concentration which is well known in comminution processes. This cushioning effect may be interpreted as a decrease in the efficiency η of the abrasion process. If we assume η to be a function of μ and in its simplest form to follow an exponential function,

All measurements have been plotted in Fig. 19 as ( Ra,c / U e2 ) against the solids loading on a double logarithmic grid. The measurements are seen to be well described by Eq. (23) with n = -0.5. It should be noted here that the range of μ and Ue which has been investigated is not large enough to permit very general conclusions to be drawn. More investigations are certainly needed in this area.

Attrition in Fluidized Beds and Pneumatic Conveying Lines 473

Figure 19. Influence of the solids loading µ on cyclone attrition. (Reppenhagen and Werther, 1997.)

However, the present results already allow a conclusion to be drawn

with respect to the solids mass flux mc,loss which is lost from the cyclone as a result of attrition inside the cyclone. From Eq. (23) it follows with n = -0.5

and with the definition of Ra,c

The cyclone inlet velocity is thus shown to be the most significant factor influencing the solids loss due to attrition in the cyclone.

5.2Attrition in the Overall Fluidized Bed System, Continuous Processes

As has been demonstrated above, there are several parts of the fluidized bed system with distinctly different attrition mechanisms. They all