Быстрай Г.П. Термодинамика открытых систем Часть 2 (2006)

Термодинамика открытых систем

ристики полученных хаотических решений.

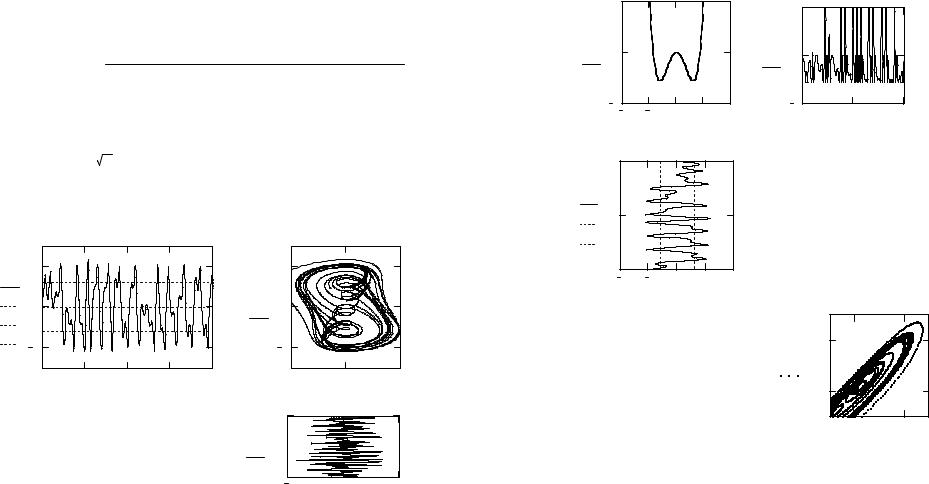
Рис.5.11. а) Динамика тока одиночного ионного канала i*(t)

– решения уравнения (5.7); б) Экспериментальная запись активности Са2+-активируемого канала при [Cа2+]=10 мкмоль/л и потенциале V=20 мВ; данные [6].

При этом, в отличие от классических методов возможности описания проводимости каналов существенно возрастают.

Задачи к главе 5

Задача 5.1. Составьте алгоритм решения уравнения (5.7), которое следует представить в виде системы трех нелинейных дифференциальных уравнений – автономной системы уравнений (5.8). Получите результаты, приведенные на рис. 5.1, или близкие к ним. Проведите анализ статистический анализ гомофазных и гетерофазных флуктуаций внутренней термодинамической силы (а)(параметра порядка), фазовый портрет (б).

Задача 5.2. Используя решения уравнения (5.7) определите хаотическую динамику скорости изменения энтропии G*, т.е. то, что представлено на рис. 5.2 (а,б)). Как ведет при этом

105

Термодинамика открытых систем

параметр порядка η (в)?

Задача 5.3. Найдите хаотические решения, приведенные на рис. 5.3. и эволюцию “расстояния” между двумя расчетными траекториями уравнения (5.7) при заданных отличающихся начальных условиях. Расстояние между двумя соседними траекто-

риями η(t)/ и η(t)// задайте величиной δη(t)= η(t)/ − η(t)// , оп-

ределите tr – характерное время, за которое система забывает начальные условия.

Задача 5.4. Научитесь строить псевдофазовые портреты решений уравнения (5.7) для для любых произвольно заданных ∆; получите частные решения, приведеные на рис.5.4.

Задача 5.5. Постройте алгоритм получения хаотической динамики параметра порядка и показателя Ляпунова λ для термодинамической системы, описываемой отображением (5.14), который приводит к результату, приведенному на рис. 5.5.

Задача 5.6. Постройте бифуркационную диаграмму η= η( a* ) для отображения сборки (5.14) в интервале

−1.6 < a* < 0.1.

ЛИТЕРАТУРА

1.Пригожин И. Введение в термодинамику необратимых про-

цессов. М.: ИЛ, 1960. С.127

2.Николис Г., Пригожин И. Самоорганизация в неравновесных системах. М.: Мир, 1973. С.511.

3.Николис Г., Пригожин И. Познание сложного. М.: Мир, 1990. С.342.

4.Гиббс Дж. Термодинамика. Статистическая механика. М.:

Наука.1982. С.488.

5.Denbigh K.G. Note on Entropy, Disorder and Disorganization. Brit. J. Sci. T. 40 ,1989, p. 323.

6.Климонтович Ю.Л. Введение в физику открытых систем. Соровский образовательный журнал.N 8,1996. С. 109-116.

7.Леонтович М.Л. Введение в термодинамику. Статистическая физика. М.: Наука, 1983. C.416.

8.Ляпунов А.М. Общая задача об устойчивости движения. 2

106

Термодинамика открытых систем

издание Л.-М., 1935. С.

9.Базаров И.П. Термодинамика. М.: Высшая школа, 1976.С.447

10.Меркин Д.Р. Введение в теорию устойчивости движения.

М.: Наука,1987.

11.Быстрай Г.П. Метод функций Ляпунова в анализе открытых термодинамических систем// Вестник кибернетики. N 4.

ИПС СО РАН 2005. С.122-137.

12.Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости и флуктуаций. М.: Мир, 1973.

С.279.

13.Семенченко В.К. Вступительная статья к книге Дьярмати И. Неравновесная термодинамика. М.: Мир, 1974. С.301.

14.Журавлев В.А. Термодинамика необратимых процессов в задачах и решениях. М.: Наука, 1979. С. 136.

15.Рубин А.Б. Биофизика. T.1. С.448. T.2. С. 467. М.: Книжный дом «Университет», 1999.

16.Gyarmati I. Оn the basic principles of the scattering processes and Its generalisation on the nonlinear promlems. Ann. D. Phys.1969, V.7. P.353.

17.Гилмор Р. Прикладная теория катастроф. М.: Мир.. 1984. T.1. С. 350. T.2. С. 285.

18.Быстрай Г.П., Пивоваров Д.В. Неравновесные системы. Свердловск: Изд-во Урал. госуни−та.1989. С.187.

19.Хакен Г. Информация и самоорганизация: макроскопический подход к сложным системам. М.: Мир, 1991. С.

20.Чернавский Д.С. Синергетика и информация. М.: Наука, 2001. С.245.

21.Кеплен С.Р., Эссиг Э. Биоэнергетика и линейная термодинамика необратимых процессов. М.: Мир, 1986. С. 382.

22.Быстрай Г.П. Методика оценки эффективности энергетических превращений в физических процессах, происходящих при воздействии на горные породы// Изв. вузов. Гор-

ный журнал.1988. N9. C.1.

23.Летников Ф.А. Синергетика геологических систем. Новоси-

бирск: Наука,1992. С.228.

24.Murray J.D. Mathematical Biology. Springer-Verlag. Berlin.

107

Термодинамика открытых систем

Heidelberg. New York. London. Paris. Tokyo. 1984.

25.Соболев С.Л. Локально-неравновесные модели процессов переноса // УФН. Т.167, N 10. C.1095

26.Лыков А.В. Тепломассообмен: (Справочник). М.: Энергия, 1978. С.480.

27.Шустер Г. Детерминированный хаос. Введение. М.: Мир. 1988. C.240.

28.Быстрай Г.П., Студенок С.И., Иванова С.И. Детерминированная модель гомофазных и гетерофазных флуктуаций в системе “жидкость−пар”// ТВТ. 2002. T.40. N 5. C. 779.

29.Быстрай Г.П., Студенок С.И., Иванова С.И. Детерминированный хаос при фазовых переходах первого рода в систе-

ме “жидкость−пар”// ТВТ. 2003. T.41. N 4. C.579.

30.Кольцова Э.М., Третьяков Ю.Д, Гордеев Л.С.и др. Нелинейная динамика и термодинамика необратимых процессов в химии и химической технологии. М.: Химия. 2001. С.407.

31.Лихтенберг А., Либерман М. Регулярная и стохастичесчкая динамика. М.: Мир. 1984. С.528.

32.Заславский Г.М. Стохастичность динамических систем. М.:

Наука, 1984. C.270

33.Быстрай Г.П. Детерминированный хаос при химических реакциях в межфазном слое при высоких температурах//

ТВТ. 2003. T.41. N 6. C.1.

34.Лифщиц E.M.,Питаевский Л.П. Физическая кинетика. Т. 10.

М.: Наука. 1979.С. 527.

35.Гельфер Я.М. История и методология термодинамики и статистической физики.Т.2. М.: Высшая школа. 1973.

36.Эткин В.А. Термокинетика (термодинамика неравновесных процессов переноса и преобразования энергии): Учебное пособие для вузов.- 2-е изд., - Тольятти, 1999.- 216 с.: илл. 17. Библиогр.: 180 назв.

37.Малинецкий Г.Г./ Хаос. Структуры. Вычислительный эксперимент. Введение в нелинейную динамику. М.: Эдиториал УРСС, 2000.

38.Пригожин И.Р. От существующего к возникающему. М.:

Наука, 1985.

108

Термодинамика открытых систем

39.Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. М.: УРСС, 2002.

40.Быстрай Г.П., Ворох А.С., Андреев С.В. Детерминированный хаос в динамике тока одиночных ионных каналов био-

мембран. Биофизика. 2005. Т.50, вып.5. с. 851-861.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Николис Г., Пригожин И. Самоорганизация в нерав-

новесных системах. М.: Мир, 1973. С.511.

Николис Г., Пригожин И. Познание сложного. М.:

Мир, 1990. С.342.

Климонтович Ю.Л. Введение в физику открытых систем. Соровский образовательный журнал.N 8,1996. С. 109116.

Базаров И.П. Термодинамика. М.: Высшая школа, 1976.С.447

Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука,1987.

Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости и флуктуаций. М.: Мир, 1973.

С.279.

Журавлев В.А. Термодинамика необратимых процессов в задачах и решениях. М.: Наука, 1979. С. 136.

Рубин А.Б. Биофизика. T.1. С.448. T.2. С. 467. М.:

Книжный дом «Университет», 1999.

Гилмор Р. Прикладная теория катастроф. М.: Мир.. 1984. T.1. С. 350. T.2. С. 285.

Кеплен С.Р., Эссиг Э. Биоэнергетика и линейная термодинамика необратимых процессов. М.: Мир, 1986. С. 382.

Гельфер Я.М. История и методология термодинамики и статистической физики.Т.2. М.: Высшая школа. 1973.

Шустер Г. Детерминированный хаос. Введение. М.:

Мир. 1988. C.240.

Кольцова Э.М., Третьяков Ю.Д, Гордеев Л.С.и др. Нелинейная динамика и термодинамика необратимых процессов в химии и химической технологии. М.: Химия. 2001.

С.407.

109

Термодинамика открытых систем

Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент. Введение в нелинейную динамику. М.: Эдиториал УРСС, 2000.

Решения задач главы 1 1.1. Оба выражения в правой части (1.11) являются непол-

ными дифференциалами, так как производство энтропии представляет только часть прироста энтропии [12,15]. Однако производство энтропии при σe=0 можно преобразовать в полный дифференциал, следуя (1.12), так как выполняется:

Это и означает, что в реальных процессах свободная энергия уменьшается, т.к. ΛF = F − F0 > 0 .Этот результат является след-

ствием используемого принципа минимальности потенциала в состоянии равновесия.

Из (1.23) получаем для полного дифференциала Пригожина−Гленсдорфа соотношение di S = −(1 / T )dF T ,V [12]. Этот

дифференциал непосредственно связан с изменением свободной энергии Гельмогольца dF. Пригожин и Гленсдорф, не доказывая этого соотношения, объясняли последнее тем, что все процессы протекают в направлении уменьшения F до тех пор, пока свободная энергия не достигнет минимума в устойчивом равновесном состоянии. Наличие такой взаимосвязи между изменениями термодинамических потенциалов для неравновесных состояний и производством энтропии в литературе как правило не обсуждается, кроме единственного упоминания в [12] о взаимосвязи свободной энергии и производства энтропии в виде указанного выше дифференциала Пригожина−Гленсдорфа.

1.2. Производство энтропии в системе как это следует из

(1.11) равно:

110

Термодинамика открытых систем

где ΛF=F−F0 – термодинамический потенциал неравновесной системы, а Λe − термодинамический потенциал внешней среды. Последнее и является ответом на вопрос в данной задаче. Если перейти к дифференциалам, то из (1.24) получаем результат, приведенный А.Б. Рубиным [15]. Аналогичные соотношения могут быть получены для других потенциалов.

1.3. После совершения одного оборота цикла через τ система вновь вернется в первоначальное состояние, следовательно скорость продуцирования энтропии, или диссипации энергии согласно (1.24), в единицу времени равна определиться уравнением (1.25). В этом случае изменение значения термодинамического потенциала неравновесной системы через время τ0 будет равно нулю ∆Λ*F τ=0. В (1.25) τ0 − время совершения одного оборота цикла (считается достаточно малым). Для внешней среды ∆Λe τ≠0, так как именно за счет взаимодействия с внешней средой и совершается оборот цикла с производимой им за это время работой. Это и доказывает что протекание неравновесных процессов в цикле сопровождается остаточными изменениями в окружающей среде.

1.4. Уравнение (1.25) позволяет сравнивать между собой различные циклы в отношении их энергетической эффективности. Действительно, если имеются две системы, для которых

∆Λ*1 = ∆Λ*2 , то при τ1< τ2 следует что β1 f β2 . Иными словами,

скорость диссипации энергии в первом цикле больше, чем во втором, при том же значении совершенной работы. Этим самым доказывается результат, полученный впервые Т. Мицунойей.

1.5. Для открытой системы энтропия может как увеличиваться так и уменьшаться со временем, так как при стремлении F→F0 функция ΛF(t) в (1.12) уменьшается во времени dΛF(t)/dt<0, а при удалении/отклонении от состояния равновесия dΛF(t)/dt>0. Таким образом, уменьшение энтропии является неустойчивым по Ляпунову процессом, т.е. оно не выполняется на бесконечном интервале времени.

111

Термодинамика открытых систем

1.6. Для доказательства выделим в структуре обратимых потоков через границу, составляющую с теплом d0S/dt:

приde/ S / dt = 0 . Из этого неравенства следует неравенство

(1.26). Неравенства типа (1.26) обычно изучаются в учебных курсах по равновесной термодинамике и приводятся без строгого доказательства.

Решения задач главы 2

2.1. Представим коэффициент Lii в виде:

Lii ( X i ) = k1 − k2 X i + k3 X i2 .

Тогда из (2.11) следует (2.12), в котором

Здесь мы учли, что принцип симметрии коэффициентов для нелинейных процессов не выполняется: Lie ≠ Lei , для уп-

рощения предполагалось выполнение равенства X c ≈ X e . Здесь

также процесс с индексом “e” “приводит в движение” процесс “i” и 0 ≤ φ ≤1 при условии, что знаки у величин сy и b1 и b2 различ-

ны. Расчеты по (2.12) показали, что кривая энергетических превращений для нелинейных процессов может лежать как выше так и ниже кривой для линейных превращений (рис. 2.4б). Числен112

В случае линейного источника имеем α=0. После интегрирования последнего уравнения получаем, что в данной задаче функ-

ция источников σe содержит слагаемые разных знаков, характеризующие стоки и источники тепла (рис.3.1):

В результате скорость изменения энтропии (кинетический потенциал) в такой задаче является сложной функцией температуры:

Можно доказать, что теорема Пригожина для описываемого уравнения выполняется, т.к. в такой нелинейной системе

имеется одно стационарное состояние при σe = const .

− σe

(αСV ρ/ T02 )

0

Термодинамика открытых систем

Рис.3.1. Зависимость нелинейного источника тепла для нелинейного уравнения теплопроводности (3.14) при

β/α = 1.2 .

Решения задач главы 4 4.2. В этом уравнении функция внешних источников равна

После интегрирования последнего уравнения получаем, что в

данной задаче функция источников σe содержит слагаемые разных знаков, характеризующие источники и стоки тепла соответственно:

В результате в такой задаче скорость изменения энтропии (кинетический потенциал) является сложной функцией температуры и содержит слагаемые разных знаков:

Характерно, что данный тип нелинейности не приводит к нарушению теоремы Пригожина при постоянных граничных услови-

ях (σe=const).

Решения задач главы 5

114