Ellinger Y., Defranceschi M. (eds.) Strategies and applications in quantum chemistry (Kluwer, 200
.pdf286 |
P. LAZZERETTI ET AL. |
where
is used to start the iteration (49)-(52). In the case of electric perturbation, denoting
by |
the coordinates of the i-th electron with charge – e , |
To first order the repulsion matrix
is obtained contracting the first-order density matrix with the two-electron integrals over the atomic basis,
The second-order density matrix
is also resolved into four components according to (46),
that is,
Accordingly, only the projections |
over the subspace of virtual orbitals are needed |
to compute the second-order density matrix.
The iterative scheme for the second-order coefficients, consistent with (49)-(52), is (in the case of electric perturbation there is no
COUPLED HARTREE-FOCK APPROACH |
287 |
The iteration starts with |
|
The second-order repulsion matrix |
is |
defined analogously to (55). |
and X matrices have been computed only once |
||
to solve the first-order CHF problem (i.e., to determine the polarizability |
and the |
||
first hyperpolarizability . |
and |
are saved onto a file to be processed at |
|
each step of the iterative calculation (63)-(66): it seems worthy of notice that the present CHF algorithm, based on the Hartree-Fock propagator (30), is quite general, compact and suitable for efficient sequential determination of both firstand secondorder perturbed orbitals. In addition, it can be easily extended to perturbations of
higher order. |
|
So far we have considered an orthonormal basis set |
In actual calculations, em- |
ploying non orthogonal sets of Gaussian functions with overlap matrix
it is customary to orthogonalize according to the Löwdin procedure, i.e.,
with similar equations for firstand second-order perturbed matrices. In the secondorder iteration eqs. (63) and (65) are replaced by
for a non orthogonal basis.
The expression for the electronic contribution to electric dipole moment,
is not affected by transformation (68)-(72), owing to the trace theorem. In addition, it can be shown that the iterative steps (49)-(52) are formally the same for a non orthogonal basis, as the formula for the polarizability
is also invariant under Löwdin orthogonalization. The overlap matrix appear only to third order in the expression for the first hyperpolarizability [10],
where |
and |
are permutations of the expression in square brackets. |
288 |
P. LAZZERETTI ET AL. |
5. Symmetry transformations of second-order density
The electron density of a molecule in the presence of electric perturbation is a scalar field with perturbation expansion [6], [11]
Relaxing the Einstein convention, sums over repeated Greek indices are made explicit in this Section, to avoid misunderstanding whenever two couples of
repeated indices |
and |
with |
, appear in a formula, compare fo r (92) hereafter. |
Introducing a basis set |
of atomic functions, for the second-order term one defines |
||
the expansion |
|
|
|
For any symmetry |
operator |
(rewritten when operating on the domain of |
|
basis functions |
for instance, the rotation-reflexion about the z-axis, with matrix |
||
representation |
|
|
|
over a basis set of Cartesian unit vectors, and belonging to a group G, one has
In the transformed coordinate system,
Hence the transformation law for second-order density is
COUPLED HARTREE-FOCK APPROACH |
289 |
Since the transformation belongs to the group G one has
and the second-order density matrices transform according to
Owing to permutational symmetry, at most six second-order matrices are independent. To account for point molecular symmetry let us introduce the symmetrized Kronecker square of T, with matrix elements [4]
Eventuallyone finds the final transformation law for the second-order density matrices
Hence, according to the present method, only the symmetry-distinct density matrices need to be computed.
Within our approach the entire molecular symmetry is exploited to increase the efficiency of the code in every step of the calculation. For a molecule belonging to
a group G of order |
|G|, only |
symmetry-distinct two-electron integrals |
over a basis set of |
Gaussian atomic functions are calculated and processed at each |
|
iteration within SCF, firstand second-order CHF procedures. A skeleton Coulomb
repulsion matrix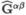 
is obtained by processing the non-redundant list of unique twoelectron integrals, then the actual repulsion matrices are obtained via the equation
This method turns out to be a major computer saver, as (i) the iterative steps become much faster, owing to the reduced number of integrals, and (ii) the occupancy of the mass storage gets smaller. Accordingly, one can afford large problems which would be otherwise intractable.
290 |
P. LAZZERETTI ET AL. |
6. Fourth-order CHF energy
The CHF formulae (75)-(77) for the response tensors are established by expanding the Hartree-Fock energy [8],
in powers of the electric field in the same way as (1). In the presence of multiple perturbations, the first-order perturbed core Hamiltonian can be written
where the parameters a, b, c, etc., are related to the intensity of each perturbation. The expansion for the energy of a molecule becomes
Comparing this general expression with the analogous expansion (1), one finds (no sum over repeated Latin indices)
It should be noted that, in this notation, the order of the superscripts is irrelevant; is the entire perturbed energy term linear in ab ... z and there is no
additional term with permuted ab ... z indices.
The following terms appear in the expression of the 4-th order energy
COUPLED HARTREE-FOCK APPROACH |
291 |
In the above formulae the projected (11) and (22) components of the density matrices are obtained from the series
Firstand second-order Fock Hamiltonians are given analogous expressions. The density corrections are given by
All of these formulae apply to the case of orthonormal basis sets [7]: corresponding expressions for the general case of metric are easily obtained via similarity transformations, see, for instance, (70).
292 |
P. LAZZERETTI ET AL. |
7. |
Second hyperpolarizability of benzene |
The computational scheme outlined in Secs. IV and V has been applied to the calculation of the hyperpolarizability of benzene molecule, for which a number of ab initio studies have been already reported [15–18]. The computer program implementing the CHF algorithm has been checked with respect to corresponding finiteperturbation theory calculations [28]. For a number of molecular systems, belonging to several point groups, the results from calculations exploiting the full symmetry have been matched with corresponding ones, obtained by using lower subsymmetries for the same molecule [11], including
In particular the results of Ref. [16], obtained via a 4-31g polarized basis set, have been reproduced on an 486 IBM compatible PC, with a hard disk memory of 100 Mbyte. As a matter of fact, in that calculation, only 1 180 752 symmetry unique
two-electron integrals |
. had to be stored within our method. |
Five large basis sets have been employed in the present study of benzene; basis set I, which has been taken from Sadlej’s tables [37], is a (10s6p4d/6s4p) contracted to [5s3p2d/3s2p], and contains 210 CGTOs. It has been previously adopted by us in a near Hartree-Fock calculation of electric dipole polarizability of benzene molecule [38].
According to our experience, Sadlej’s basis sets [37] provide accurate estimates of first-, second-, and third-order electric properties of large molecules [39].
Basis sets II-V have been employed in estimating the Hartree-Fock limit of a number of second-order properties in the benzene molecule [40]. The primitive GTO sets range from (11s7 p 2 d /5 s 2 p ) to (14s8p4d/8s3p), contracted respectively to [6s5p1d/3s1p] and [9s6p4d/6s3p]. Although the exponents for the polarization functions of these basis sets were chosen in that paper to maximize the paramagnetic susceptibility, the extension of the basis sets (from 252 to 396 CGTO) guarantees a remarkable
flexibility and excellent overall characteristics. |
The number |
of symmetry unique |
two-electron integrals range from |
The calculations have been carried |
|
out on a CONVEX C-220 and on an IBM 3090. |
|
|
The ability of Sadlej basis sets [37] to provide reliable values of |
has been tested |
|
in a limited number of cases with encouraging results [11]. In the present work on benzene the Sadlej basis set yields theoretical estimates close to those obtained by
Perrin et al. [16] and Kama et al. [17], but smaller than those reported by Augspurger and Dykstra [18]. The C-C bond distance retained in [18], however, is compared to used by us, see Refs. [38] and [40].
The theoretical results provided by the large basis sets II-V are much smaller than those from previous references [15–18]: the present findings confirm that the secondhyperpolarizability is largely affected by the basis set characteristics. It is very difficult to assess the accuracy of a given CHF calculation of and it may well happen that smaller basis sets provide theoretical values of apparently better quality. Whereas the diagonal components of the electric dipole polarizability are quadratic properties for which the Hartree-Fock limit can be estimated with relative accuracy a posteriori, e.g., via extended calculations [38], it does not seem possible to establish a variational principle for, and/or upper and lower bounds to, either 
and
As a matter of fact, the electric dipole polarizabilities obtained via basis sets II-IV are larger than those reported in Ref. 16 and Ref. 18: from Table 1 of Ref. 39 it can
be seen that |
from those basis sets ranges from 78.352 to 79.142 a.u., and that |
COUPLED HARTREE-FOCK APPROACH |
293 |
ranges from 42.305 to 45.284 a.u.. Sadlej basis sets give _ and
a.u., see Table 2 in Ref. [39]. These results are close to the estimated Hartree-Fock
limits, |
,, and |
[39]; accordingly they are much more accurate |
||
than those reported by Perrin et al. |
[16], i.e., |
and |
Our |
|
estimates are also more accurate than the best ones from Ref. |
18, |
and |
||
These findings imply that our basis sets are definitely more reliable than those adopted in Ref. 16 and Ref. 18 for studying second-order electric properties. Accordingly, it seems quite difficult to understand that theoretical obtained via relatively small ad hoc basis sets are closer to the HF limit, if the same basis sets provide less accurate polarizabilities. This feature would mean that the problem of constructing suitable basis sets for the simultaneous evaluation of second-, third-, and fourth-rank electric properties of HF quality ought to be carefully reconsidered. Comparison with a few experimental values, obtained corresponding to different wavelengths [41–47], seems however to suggest that nuclear vibration [3] and electron correlation [15–18] play an important role. In particular, the correlation contributions estimated via second-order Moeller-Plesset techniques [16] are large. Accordingly, the present work confirms that CHF level of accuracy is insufficient to predict accurate hyperpolarizability of benzene molecule.
In any event, we are confident that the computational approach developed in this study, owing to its efficient use of molecular symmetry, can help develop large basis sets for first and second hyperpolarizabilities. An important aim would be that of estimating, at least at empirical level, Hartree-Fock limits for these quantities. To this end the use of basis sets polarized two times, according to the recipe developed by Sadlej [37], would seem very promising.
294 |
P. LAZZERETTI ET AL. |
Acknowledgments
The authors wish to thank Dr. T. Prosperi for discussions. Financial support from the C.I.C.A.I.A. of the University of Modena, from the Italian M.U.R.S.T., and the Comitato Nazionale Scienze e Tecnologia dell’Informazione of the Italian C.N.R. is gratefully acknowledged.
References
1.A. D. Buckingham, Adv. Chem. Phys. 12, 107 (1967); A. D. Buckingham and B. J. Orr, Quart. Rev. 21, 195 (1967); M. P. Bogaard and B. J. Orr, in Molecular Structure and Properties, Int. Rev. Sci., Phys. Chem. Series 2, Vol.
2, A. D. Buckingham Ed., Butterworths, London 1975.
2.P. A. Franken and J. F. Ward, Rev. Mod. Phys. 35, 23 (1963); J. F. Ward, Rev.
Mod. Phys. 37, 1 (1965); J. Orr and J. F. Ward Molec. Phys. 20, 513 (1971);
C.K. Miller, B. J. Orr, and J. F. Ward, J. Chem. Phys. 67, 2109 (1977).
3.D. M. Bishop, Rev. Mod. Phys. 62, 343 (1990); J. Chem. Phys. 86,
5613 (1987); ibid. 90, 3192 (1989); ibid. 95, 5489 (1991); Phys. Rev. Let- ters 61, 322 (1988); Chem. Phys. Letters 153, 441 (1988).
4.R. McWeeny, Symmetry, Pergamon, Oxford, 1963.
5.S. J. Cyvin, J. E. Rauch, and J. C. Decius, J. Chem. Phys. 43, 4083 (1965).
6.P. Lazzeretti and R. Zanasi, Int. J. Quantum Chem. Phys. 15, 645 (1979).
7.R. McWeeny, Phys. Rev. 126, 1028 (1962); G. F. Diercksen and R. McWeeny,
J.Chem. Phys. 44, 3554 (1966); R. McWeeny, Chem. Phys. Letters 1, 567 (1968); J. L. Dodds, R. McWeeny, W. T. Raynes, and J. P. Riley, Molec.
Phys. 33, 611 (1977); J. L. Dodds, R. McWeeny, and A. J. Sadlej, Molec. Phys.
34, 1779 (1977).
8.R. E. Wyatt and R. G. Parr, J. Chem. Phys. 41, 514 (1964).
9.G. J. B. Hurst, M. Dupuis, and E. Clementi, J. Chem. Phys. 89, 385 (1988).
10.P. Lazzeretti and R. Zanasi, Chem. Phys. Letters 39, 323 (1976); J. Chem.
Phys. 74, 5216 (1981).
11.P. Lazzeretti, M. Malagoli, and R. Zanasi, Z. Naturforsch., in the press
12.P. A. Christiansen and E. A. McCullough Jr., Chem. Phys. Letters 63,
570 (1979).
13.J. Zyss and G. Berthier, J. Chem. Phys. 77, 3635 (1982).
14.C. Daniel and M. Dupuis, Chem. Phys. Letters 171, 209 (1990).
15.G. P. Das and D. S. Dudis, Chem. Phys. Letters 185, 151 (1991).
16.E. Perrin, P. N. Prasad, P. Mougenot, and M. Dupuis, J. Chem. Phys. 91,
4728 (1989).
17.S. P. Karna, G. B. Talapatra, and P. N. Prasad, J. Chem. Phys. 95, 5873
(1991).
COUPLED HARTREE-FOCK APPROACH |
295 |
18.J. D. Augspurger and C. E. Dykstra, Molec. Phys. 76, 229 (1992).
19.S. P. Karna, and M. Dupuis, J. Comput. Chem. 12, 487 (1991).
20.J. Perez and M. Dupuis, J. Phys. Chem. 95, 6525 (1991).
21.J. E. Bloor, J. Molec. Struct. (THEOCHEM) 234, 173 (1991).
22.P. Chopra, L. Carlacci, H. F. King, and P. N. Prasad, J. Phys. Chem. 93, 7120 (1989).
23.G. Maroulis, J. Chem. Phys. 94, 1182 (1991); ibid. 96, 6048 (1992); Chem. Phys. Letters 195, 85 (1992).
24.G. Maroulis and A. J Thakkar, J. Chem. Phys. 93, 4164 (1990).
25.M. Dory, L. Beudels, J. G. Fripiat, J. Delhalle, J. M. André, and M. Dupuis, Int. J. Chem. 42, 1577 (1992).
26.B. L. Hammond and J. E. Rice, J. Chem. Phys. 97, 1138 (1992).
27.G. Maroulis and D. M. Bishop, Chem. Phys. Letters 128, 462 (1986); Molec. Phys. 58, 273 (1986); Theor. Chim. Acta 69, 161 (1986).
28.R. J. Bartlett and G. D. Purvis III, Phys. Rev. A20, 1313 (1979).
29.L. Adamowicz and R. J. Bartlett, J. Chem. Phys.84, 4988 (1986).
30.H. Sekino and R. J. Bartlett, J. Chem. Phys. 94, 3665 (1991).
31.W. A. Parkinson and J. Oddershede, J. Chem. Phys. 94, 7251 (1991).
32.G. J. M. Velders, J. M. Gillet, P. J. Becker, and D. Feil, J. Phys. Chem. 95, 8601 (1991).
33.J. E. Rice, P. R. Taylor, T. J. Lee, and J. Almlöf, J. Chem. Phys. 94, 4972 (1991).
34. G. Berthier, M. Defranceschi, P. Lazzeretti, G. Tsoucaris, and R. Zanasi,
J. Molec. Struct. (THEOCHEM) 254, 205 (1992).
35.S. P. Karna, P. N. Prasad, and M. Dupuis, J. Chem. Phys. 94, 1171 (1991).
36.S. T. Epstein, The Variation Method in Quantum Chemistry, Academic, New York, 1974.
37.A. J. Sadlej, Coll. Czech. Chem. Comm. 53, 1995 (1988).
38.P. Lazzeretti, M. Malagoli, and R. Zanasi, Chem. Phys. Letters 167, 101 (1990).
39.P. Lazzeretti and J. A. Tossell, J. Molec. Struct. (THEOCHEM) 236, 403 (1991).
40.P. Lazzeretti, M. Malagoli, and R. Zanasi, J. Molec. Struct. (THEOCHEM) 234, 127 (1991).
41.P. Bogaard, A. D. Buckingham, and G. L. D. Ritchie, Molec. Phys. 18, 575 (1970).
42.J. P. Hermann, Opt. Comm. 9, 74 (1973).
43.M. D. Levenson and N. Bloembergen, J. Chem. Phys. 60, 1323 (1974).
44.M. D. Levenson and N. Bloembergen, Phys. Rev. B 10, 4447 (1974).