2.11. Помехоустойчивость приема многопозиционных сигналов

Помехоустойчивость приема ортогональных сигналов. Вероятность правильного приемаi-го сигнала

(3.59)

Здесь m-мерная плотность вероятностей случайных величинu₁,u₂, …u_m при условии, что передавался сигнал. Вероятность ошибки при приемеi-го сигнала

(3.60)

Сигнал на выходе i-го канала

представляет гауссовскую случайную величину с математическим ожиданием и дисперсиейСигналы на выходах остальных каналов также являются гауссовскими случайными величинами с той же дисперсиейи только математические ожидания равны нулю. Случайные величиныс учетом (3.58) не коррелированны, а поскольку эти величины также являются гауссовскими, то они и независимы. Таким образом,m-мерная плотность вероятности

, (3.61)

где

, (3.62)

(3.63)

Подставив (3.61) в (3.59) с учетом (3.62) и (3.63) и в соответствии с преобразованиями, приведенными в [13], получим вероятность правильного приема i-го сигнала

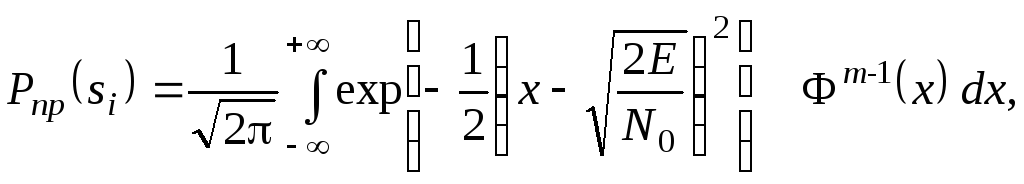(3.64)

где интеграл вероятности.

Полная вероятность ошибки при различении mравновероятных сигналов, то есть, определяется выражением

(3.65)

При сравнении систем необходимо иметь в виду, что при фиксированной длительности элемента сигнала Ткаждый равновероятныйm–ичный сигнал несет враз больше количества информации, чем двоичный сигнал. На рисунке 3.35 приведены кривые помехоустойчивости когерентного приема ортогональных сигналов приm=2, 4, 32 и 256. Для сравнения приведена кривая, характеризующая помехоустойчивость когерентного приема детерминированного бинарного ФМн радиосигнала. Здесьэнергия, затрачиваемаяна один бит информации.

Помехоустойчивость приема симплексных сигналов. Напомним, что симплексные сигналы образуют ансамбль изmодинаково коррелированных сигналов с коэффициентом корреляции .Минимальное расстояние, если сигналы имеют одинаковые энергии, равно

,

откуда понятно, что минимальное расстояние ортогональных сигналов , а для симплексных сигналов, то есть для достижения одной и той же помехоустойчивости приема симплексных сигналов требуется энергии сигналов враз меньше, чем для ортогональных сигналов. Таким образом, вероятность ошибки для симплексных сигналов определяется как

(3.66)

Помехоустойчивость симплексных сигналов выше, чем ортогональных. Однако это различие уменьшается с увеличением m, и приm>>1 помехоустойчивость обоих ансамблей оказывается практически одинаковой.

Помехоустойчивость приема биортогональных сигналов.Биортогональные сигналы формируются изортогональных сигналов дополнением их сигналами, противоположными ортогональным. Этим достигается понижение сложности демодулятора (уменьшение количества каналов в два раза). Вероятность правильного приема любого сигнала

Проведя рассуждения, аналогичные для ортогональных сигналов, можно получить выражение для вероятности ошибки биортогональных сигналов:

(3.67)

Помехоустойчивость приема биортогональных сигналов выше, чем ортогональных, однако при m >>2 эта разница становится пренебрежимо малой.

Сравнение помехоустойчивости приема когерентного и некогерентного приемаортогональных сигналов показывает, что приm=128 различие в помехоустойчивости практически отсутствует. На практике при малой вероятности ошибки приема часто пользуются верхней границей помехоустойчивости

. (3.68)