5.2.2. Последовательный шпс

Наиболее широкое применение из класса последовательных ШПСв радиосистемах нашли двоичные одночастотные сигналы с фазовой манипуляцией. Фаза данного сигнала изменяется по закону некоторой модулирующейпсевдослучайной последовательности(ПСП). При двоичной манипуляции фаза принимает два значения:

где {d_ki} -кодовая последовательностьk-го варианта сигнала.

Аналитическое выражение k-го варианта последовательного ШПС с двоичной фазовой манипуляцией имеет вид:

Здесь T = L_э,_э- длительность элементарного сигнала,A- амплитуда,_н- несущая частота,₀- некоторая начальная фаза,

Устройство формирования сигнала (5.4) приведено рис. 5.5. Оно содержит: генератор коротких тактовых импульсов Г₁с периодомT ; схему формирования кодовой последовательности импульсов (ФКП) реализующий множитель в фигурных скобках ; генератор Г₂гармонических колебаний частоты_ни модулятор (перемножитель).

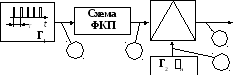s_k(t)

4

12

3

Рис. 5.5. Устройство формирования последовательного

ШПС с фазовой манипуляцией

Процесс формирования k-го варианта последовательного ШПС с двоичной фазовой манипуляцией в различных точках устройства показан на рис. 5.6.

1T

2 _э

0 0 0 1 1 0 1

3

4

Рис. 5.6. Формирование k-го варианта последовательного ШПС

с двоичной фазовой манипуляцией

База последовательного ШПС равна числу элементов сложного сигнала и определяется как

Широкое применение в радиосистемах последовательных ШПС с двоичной фазовой манипуляцией объясняется их хорошими корреляционными свойствами, возможностью получения значительного числа вариантов сигнала для L = constи кроме того сравнительной простотой реализации устройства формирования и демодуляции на элементах цифровой микроэлектронной техники.

В настоящее время для двоичной фазовой манипуляции в последовательных ШПС используются, как правило, коды Баркера, последовательности Голда, последовательности Хаффмена (или М-последовательности), нелинейные составные и другие последовательности, которые позволяют получать хорошие спектральные и корреляционные характеристики сигнала.

5.2.3. Последовательно-параллельные шпс

Наибольшее применение из последовательно-параллельных ШПС нашли сигналы с псевдослучайной перестройкой рабочей частоты (ППРЧ). Такие сигналы образуются в результате скачкообразного изменения несущей частоты по закону ПСП при постоянной амплитуде и шаге квантования по времени и частоте.

В сигналах с ППРЧ рабочая частота может изменяться несколько раз за время передачи одного бита информации (быстрая ППРЧ) или один раз за время передачи нескольких бит (медленная ППРЧ). Для быстрой ППРЧ аналитическое выражение k-го варианта сигнала можно записать в виде

где T=L_э,_э- длительность элементарного сигнала, определяемая шагом дискретизации по времени,_k- минимальный частотный сдвиг несущей, определяемый шагом дискретизации по частоте и обычно выбираемый из условия кратности ширине спектра одного импульса длительностью_э

для любого kчастоты_k=,l_ki- некоторые целые числа (задающие кодообразование частоты),_ki- начальные фазыi-х составляющихk-го варианта сигнала (если_kiкратны 2, в сигнале (5.5) нет скачков фазы при переходе от одного элементарного сигнала к другому). Выбор_kв соответствии с (5.6) позволяет обеспечить условие ортогональности каждогоk-го сигнала в (5.5).

Частотно-временная матрица k-го варианта сигнала и соответствующая ей диаграмма трехэлементного сигнала без скачка начальной фазы приведена на рис. 5.7. На рис. 5.8 изображен спектр последовательно-параллельного ШПС, когдаiпоследовательно принимает значения 1, 2, ... ,L, а частотный сдвиг = = 2 /_э. Результирующая спектральная плотность сигнала образуется как результат суперпозиции спектров отдельных импульсов.

Полоса частот занимаемая спектром на рис. 6.8 можно определить соотношением

Поскольку обычно  = 2 /_эиT=L_э, то для базы сигнала с ППРЧ имеем

Рис. 5.7. Частотно-временная матрица и диаграмма трехэлементного

последовательно-параллельного ШПС с ППРЧ

Рис. 5.8. Спектральная плотность последовательно-параллельного ШПС

с L частотами элементами

При условии L  1 получаемB  L². То есть база последовательно - параллельного ШПС с ППРЧ примерно равна квадрату от количества составляющих сложного сигнала.