2.1.Синтез реляционных баз данных.

База данных состоит из множества атрибутов и ключей. С точки зрения теоретико-множественного описания реляционной базой данных d называется такая совокупность отношений {R₁, R₂, ...,R_p}, в которой каждое отношение имеет вид R_i= (S_i,K_i), где S_i- множество атрибутов, а K_i - множество атрибутов образующих ключ.

Предположим на входе задано множество F- зависимостей F над R. С их помощью требуется создать базу данных R=( R₁, R₂, ...,R_p). Эта БД должна удовлетворять следующим требованиям:

1. Множество F полностью характеризуется с помощью R , т.е.

где К – выделенный ключ R_i.

2. Каждое отношение R_i находится в третьей нормальной форме.

3. Не существует базы данных с меньшим числом отношений, удовлетворяющим пунктам 1 и 2.

4. Соединение всех полученных отношений R_i дает исходное отношение R.

Алгоритм порождающий базу данных из заданных F-зависимостей называется алгоритмом синтеза.

Определение. Если R – база данных и на ней задано множество F-зависимостей G, то в ней существует по крайней мере |E_G| отношений. Это означает, что в R столько же отношений, сколько и классов эквивалентности. Из этого следует следующее.

Пусть F - множество F – зависимостей. Любая база данных должна иметь |E_F’| отношений, где F’ неизбыточное покрытие для F.

Исходя из этого строится способ построения структуры базы данных.

Сначала находится неизбыточное покрытиеF’ для F и в E_F’ вычисляем классы эквивалентности. Для каждого E_F’(X) строим отношение, состоящее из всех атрибутов, появляющихся в E_F’(X). При этом атрибуты левой части каждого класса эквивалентности образуют выделенный ключ.

Реализация этого способа позволяет получить следующий алгоритм:

Вход: множество F – зависимостей F над R.

Выход: полная схема баз данных для F.

1. Наити для F редуцированное минимальное покрытие G.

2. Для каждойCF – зависимости (X₁,X₂,…,X_k) Y из G построить отношение R_j= X₁X₂…X_kY с выделенными ключами K={X₁,X₂,…X_k).

3. Вернуться к п. 2.

Для всякой предметной области можно построить несколько эквивалентных F-описаний. Опираясь на некоторое исходное F-описание заданной предметной области, можно найти для F эквивалентное неизбыточное представление. Неизбыточное представление – представление, лишенное избыточных ФЗ и посторонних атрибутов. Для этого существуют соответствующие алгоритмы «чистки» F-описания.

«Чистка» исходного F-описания выполняется в два этапа:

1. вначале из F удаляются все избыточные ФЗ (они логически следуют из оставшихся). Полученное в результате множество ФЗ называют неизбыточным покрытием F и обозначают F_неизб;

2. далее из F_неизб удаляются посторонние атрибуты. Этот процесс называется редуцированием, а полученное в результате множество ФЗ называется редуцированным покрытием и обозначается F_ред.

Множество ФЗ F_ред. не всегда является самым экономным (оптимальным) представлением семантической структуры предметной области. Тем не менее, использование F_ред. для синтеза схемы БД обеспечивает в достаточной мере неизбыточность получаемой БД.

Известно, что к организации БД предъявляются три требования: неизбыточность, непротиворечивость, независимость. Последнее из них – независимость данных от приложений достигается в основном средствами СУБД. Неизбыточность и непрворечивость БД можно обеспечить путём выбора подходящей схемы БД.

В теории нормализации доказано, что БД будет неизбыточной и средствами СУБД можно достичь её непротиворечивого состояния, если её схема будет эффективной относительно заданного F-описания предметной области.

Пусть R – множество имен атрибутов, значения которых требуется хранить в БД, и F – множество ФЗ, описывающих связи между атрибутами.

Схема БД над R называется эффективной относительно F, если:

1. она сохраняет F (разбиение R на R₁, R₂, …, R_m не приводит к потере зависимостей из F, а значит, связей между атрибутами);

2. обладает свойствами соединения без потерь информации (представления БД в виде одной таблицы r(R) или в виде совокупности таблиц r₁(R₁), r₂(R₂), …, r_m(R_m) равносильны). Последнее означает, что любое допустимое состояние таблицы r(R) всегда можно получить из таблиц r₁(R₁), r₂(R₂), …, r_m(R_m) с помощью операции естественного соединения

к(К) = к₁(К₁) к₂(К₂) …к_ь(К_ь)

3) все подсхемы R_iρ нормализованы, то есть находятся в НФБК(нормальной форме Бойса–Кодда). Это означает, что всякая ФЗ, действующая в рамках таблицы r_i(R_i) в левой части имеет ключ таблицы r_i(R_i), i =1, 2, …, m.

Теорема. Для любого множества ФЗ F, заданного на конечном множестве атрибутов R, всегда существует схема БД

обладающая свойством соединения без потерь, сохраняющая все ФЗ из F и находящаяся в 3НФ.

Свойства схемы БД, удовлетворяющей условиям данной теоремы, вполне приемлемы для практики, так как они гарантируют непротиворечивость БД. 3НФ допускает определённое избыточное дублирование данных, но с этим приходится мириться и учитывать в программах ввода и редактирования данных.

На рисунке 1.1 показана схема получения БД методом синтеза.

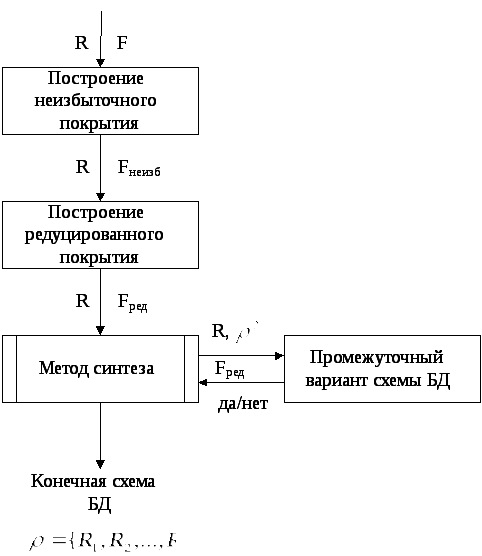
Рис.1.1. Схема получения БД методом синтеза.