6. Оценка погрешности прямых и косвенных многократных измерений

Оценка погрешности прямых многократных измерений

При оценке погрешности прямых многократных измерений рекомендуется принять следующий порядок выполнение операций.

1. Проводятся измерения заданного физического параметра n раз в одинаковых условиях, и результаты записываются в таблицу.

2. Если результаты некоторых измерений резко отличаются по своему значению от остальных измерений, то они как промахи отбрасываются, если после проверки не подтверждаются.

3. Вычисляется среднее арифметическое 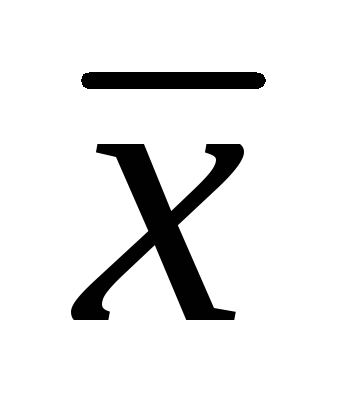изn одинаковых измерений. Оно принимается за наиболее вероятное значение измеряемой величины

. (8)

4. Находятся абсолютные погрешности отдельных измерений

5. Вычисляются квадраты абсолютных погрешностей отдельных измерений (Δх_i)²

6. Определяется средняя квадратичная ошибка среднего арифметического

.

7. Задается значение доверительной вероятности Р. В лабораториях практикума принято задавать Р=0,95.

n	Р				n	Р
	0,8	0,9	0,95	0,98		0,8	0,9	0,95	0,98
3	1,9	2,9	4,3	7,0	6	1,5	2,0	2,6	3,4
4	1,6	2,4	3,2	4,5	7	1,4	1,9	2,4	3,1
5	1,5	2,1	2,8	3,7	8	1,4	1,9	2,4	3,9

8. Находится коэффициент Стьюдента для заданной доверительной вероятности α и числа произведенных измерений (см.табл.)

9. Определяется случайная погрешность

.

10. Определяется суммарная погрешность

,

где δх – приборная погрешность, Δх – случайная погрешность.

11. Оценивается относительная погрешность результата измерений

.

12. Записывается окончательный результат в виде

, с α=… Е=…%.

Окончательный результат измерений рекомендуется представлять в следующем виде

, Р=…, Е=…(7)

Следует иметь в виду, что сами формулы теории ошибок справедливы для большого число измерений. Поэтому значение случайной, а следовательно, и суммарной погрешности определяется при малом n с большой ошибкой. При вычислении Δх при числе измерений рекомендуется ограничиваться одной значащей цифрой, если она больше 3 и двумя, если первая значащая цифра меньше 3. Например, если Δх= 0,042, то отбрасываем 2 и пишем Δх=0,04, а если Δх=0,123, то пишем Δх=0,12.

Число разрядов результата и суммарной погрешности должно быть одинаковым. Поэтому среднее арифметическое погрешности должно быть одинаковым. Поэтому среднее арифметическое вычисляется вначале на один разряд больше, чем измерение, а при записи результата его значение уточняется до числа разрядов суммарной ошибки.

Оценка погрешности косвенных многократных измерений

При оценке погрешности косвенных многократных измерений , являющейся функцией других независимых величин, можно использовать два способа.

Первый способ используется, если величина y определяется при различных условиях опыта. В этом случае для каждого из значений вычисляется, а затем определяется среднее арифметическое из всех значенийy_i

.

Систематическая (приборная) погрешность находится на основании известных приборных погрешностей всех измерений по формуле. Случайная погрешность в этом случае определяется как ошибка прямого измерения.

Второй способ применяется, если данная функция y определяется несколько раз при одних и тех же измерений. В этом случае величина рассчитывается по средним значениям.. Систематическая (приборная) погрешность, как и при первом способе, находится на основании известных приборных погрешностей всех измерений по формуле

,

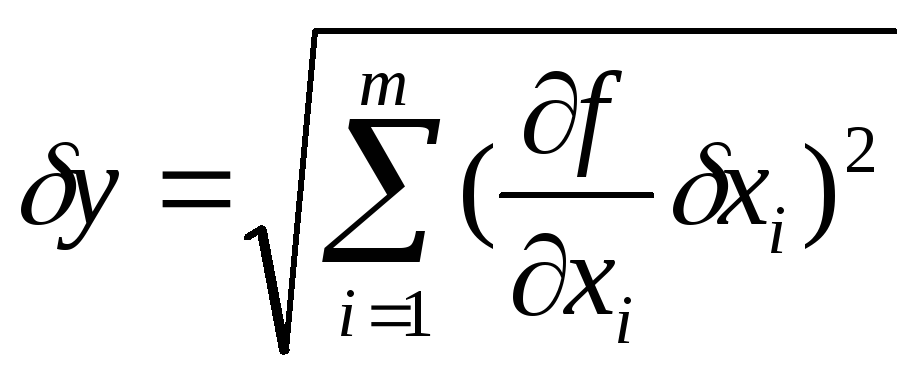где - приборные ошибки прямых измерений величины,- частные производные функции по переменной.

Для нахождения случайной погрешности косвенного измерения вначале рассчитываются средние квадратичные ошибки среднего арифметического отдельных измерений. Затем находится средняя квадратичная ошибка величины y. Задание доверительной вероятности α, нахождение коэффициента Стьюдента , определение случайной и суммарной ошибок осуществляются так же, как и в случае прямых измерений. Аналогичным образом представляется результат всех расчетов в виде

, с Р=… Е=…%.

Пример, получим формулу для расчета систематической погрешности при измерении объема цилиндра. Формула вычисления объема цилиндра имеет вид

.

Частные производные по переменным d и h будут равны

, .

Таким образом, формула для определения абсолютной систематической погрешности при измерении объема цилиндра имеет следующий вид

,

где иприборные ошибки при измерении диаметра и высоты цилиндра

Пример: Определить погрешность мощности, которая рассеивается в резисторе по формуле со следующими величинами тока и сопротивления резистору, которые определяются прямым измерением: R = 1,10 ± 0.05 Ом ; I = 1,20 ± 0.05 A. Результаты приведены со средними квадратичными отклонениями средних арифметических R и I. Оценка истинного (среднего) значения мощности:

Вт

Для оценки точности полученного значения вычисляем частичные производные и частичные погрешности косвенных измерений:

= 1,2²·0,05=0,072 А² Ом;

=2·1,2·1,1·0,05= 0,132 А² Ом 

Среднее квадратичное отклонение косвенного измерения мощности , которое вычислено за формулой составляет

=0,15 А² Ом  =0,15 Вт.

Р = 1,58 ± 0.15 Вт.