
- •Билет 1
- •2.Геометрические преобразования в трехмерной графике. Матрицы преобразования.
- •Трехмерные аффинные преобразования
- •3. Составить электрическую схему автоматизированного рабочего места инженера на базе пэвм
- •Билет 2
- •Билет 3
- •2. Понятие телеобработки. Терминальная и системная телеобработка
- •1. 1 Основные положения телеобработки данных
- •1. 2 Системная телеобработка данных
- •1. 3 Сетевая телеобработка данных
- •Билет 4
- •2.2. Структура и состав экспертной системы
- •Структура базы знаний
- •Механизм логического вывода.
- •Модуль извлечения знаний.
- •Система объяснения
- •Билет 5
- •1. Целочисленные задачи и методы их решения.
- •2. Открытые вычислительные сетевые структуры. Эталонная модель
- •3. Записать алгоритм решения системы линейных уравнений методом итераций
- •2. Открытые вычислительные сетевые структуры. Эталонная модель
- •Эталонная модель osi
- •Уровень 1, физический
- •Уровень 2, канальный
- •Уровень 3, сетевой
- •Протоколы ieee 802
- •3. Записать алгоритм решения системы линейных уравнений методом итераций
- •Билет 6
- •2. Окна в компьютерной графике. Алгоритмы преобразования координат при выделении, отсечении элементов изображения.
- •3. Как определить информацию о памяти (размер озу ...)
- •Билет 7
- •1. Понятие структурной организации эвм
- •2. Проекции в трехмерной графике. Их математическое описание. Камера наблюдения.
- •Билет 8
- •Основные подходы к разработке по. Методы программирования и структура по.
- •Билет 9
- •2. Принципы построения и функционирования эвм. Принцип программного управления.
- •3. Алгоритм определения скорости передачи с нгмд на нжмд
- •Билет 10
- •1. Организация диалога в сапр
- •2. Видеоконтроллеры, их стандарты для пэвм типа ibm pc.
- •3. Текстуры в машинной графике.
- •3. Текстуры в машинной графике.
- •2. Афинное
- •Билет 11
- •3. Реалистичная графика. Обратная трассировка луча.
- •Билет 12
- •2. Цвет в машинной графике. Аппроксимация полутонами.
- •Алгоритм упорядоченного возбуждения
- •3. Представить алгоритм определения тактовой частоты цп
- •Билет 13
- •1. Структурное программирование при разработке программы.
- •2. Понятие критерия оптимального проектирования и его связь с варьируемыми переменными через уравнения математической модели. Постановка задачи оптимального проектирования.
- •3. Представить алгоритм определения быстродействия нгмд в режиме записи данных.
- •2. Понятие критерия оптимального проектирования и его связь с варьируемыми переменными через уравнения математической модели. Постановка задачи оптимального проектирования.
- •3. Представить алгоритм определения быстродействия нгмд в режиме записи данных.
- •Билет 14
- •3. Таблицы истинности, совершенные нормальные формы представления булевых функций
- •Бинарные функции
- •2. Задачи безусловной и условной оптимизации
- •2. Классификация центральных процессоров Intel и соответствующих локальных и системных шин пэвм типа ibm pc
- •3. Реалистичная графика. Обратная трассировка луча.
- •Билет 16
- •Построение с использованием отношений
- •Построение с использованием преобразований
- •3.Составить алгоритм поиска экстремума функции двух переменных
- •Билет 17
- •1.Методы представления знаний в экспертных системах
- •2.4.2 Искусственный нейрон
- •2.Устройства автоматизированного считывания графической информации (сканеры). Конструкция и основные характеристики.
- •3. Составьте программу для определения скорости передачи информации по сети одной эвм к другой.
- •Билет 18
- •1. Системно-сетевая телеобработка
- •2. Тестирование программ.
- •Билет 19
- •3. Графические форматы. Bmp, gif и jpeg.
- •1. Понятие алгоритма. Свойства. Способы записи.
- •2. Построение реалистичных изображений. Алгоритм построения теней в машинной графике.
- •3. Представить алгоритм определения быстродействия нгмд в режиме чтения данных.
- •Билет №21
- •3. Приоритетные методы удаления скрытых поверхностей. Bsp – деревья.
- •Билет 22
- •2.Методы проверки работоспособности объектов на этапе проектирования: "наихудшего случая" и имитационного моделирования
- •1. Метод наихудшего случая
- •2. Метод имитационного моделирования
- •Билет 23
- •1. Функциональные узлы последовательностного типа: регистры, триггеры, счетчики.
- •2. Назначение, классификация математических моделей и методы их построения. Проверка адекватности математических моделей
- •3. Алгоритмы сжатия графических данных.
- •Асинхронный rs – триггер.
- •Синхронный rs–триггер.
- •Синхронный д-триггер
- •Счетный т-триггер.
- •Двухступенчатые триггеры.
- •Счетчики.
- •Классификация счетчиков.
- •Регистры
- •2. Назначение, классификация математических моделей и методы их построения. Проверка адекватности математических моделей.
- •Билет 24
- •1. Математические модели процессов теплопереноса.
- •1 Вариант
- •2 Вариант-
- •2.Интерполяционные кривые в машинной графике.
- •Билет 25
- •1. Трансляторы. Виды. Состав.
- •2. Технические средства диалога машинной графики (световое перо, мышь, шар, джойстик). Конструкция основные характеристики
- •3. Записать алгоритм решения нелинейного уравнения методом Ньютона.
- •Билет 26
- •1. Автоматизация методов управления, вариантного, адаптивного и нового планирования в астпп.
- •2. Модели гидродинамики
- •3. Записать алгоритм поиска экстремума функции Розенброка овражным методом.
- •Автоматизация метода вариантного планирования
- •Автоматизация метода адаптивного планирования тпп
- •Автоматизация метода нового планирования тпп
- •Оптимизация проектирования сборочных процессов
- •1.Модель гидродинамики идеальной смешение:
- •3. Гидродинамические диффузионные модели.
- •4.Гидродинамическая модель ячеечного типа.
- •3. Записать алгоритм поиска экстремума функции Розенброка овражным методом.
- •Билет 27
- •Общая интерпретация реляционных операций
- •Билет 28
- •1.Понятие языков программирования и их классификация. Жизненный цикл программы.
- •2.Реляционная модель данных. Сравнение с иерархической и сетевой моделями.
- •3.Написать алгоритм вычисления определенного интеграла методом трапеций.
- •2. Реляционная модель данных. Сравнение с иерархической и сетевой моделями.
- •3.Написать алгоритм вычисления определенного интеграла методом трапеций.
- •Билет 29
- •2. Декомпозиция отношений. Первая, вторая и третья нормальные формы.
- •3. Записать алгоритм поиска экстремума функции
- •Билет 30
- •2. Декомпозиция отношений. Первая, вторая и третья нормальные формы.
- •3. Написать алгоритм вычисления определенного интеграла методом трапеций.
- •Билет 31
- •Выбор компонентов
Билет 24
Математические модели процессов теплопереноса.
Интерполяционные кривые в машинной графике.
Представить алгоритм определения производительности работы ЦП по тестируемой команде.
1. Математические модели процессов теплопереноса.
1 Вариант
Теплопроводность распространение тепла за счет колебательных движении атомов и молекул. Наблюдается в твердых телах и тонких неподвижных слоях жидкости и газа. Теплопроводность описывается законом Фурье:
![]() ,
где dq
– количество тепла, переданное в единицу
времени через площадь dF;
,
где dq
– количество тепла, переданное в единицу
времени через площадь dF;
![]() - коэффициент теплопроводности.
- коэффициент теплопроводности.
Изменение температуры в любой точке объема в любой момент времени можно найти из уравнения теплопроводности вида:
![]()
Конвективный теплоперенос – тепло передается из-за разности плотностей. Такой способ пердачи тепла возможен для жидкостей и газов. Описывается уравнением теплоотдачи:
![]()
![]() - коэффициент
теплоотдачи
- коэффициент
теплоотдачи
Передача тепла от одной среды к другой через бесконечно плоскую стенку.
П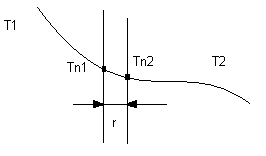 оток
тепла от теплоносителя передается
стенке в следствие теплопередачи. Этот
же поток тепла передается через стенку
в следствие теплопроводности. Далее он
передается хладоагенту в следствие
теплоотдачи
оток
тепла от теплоносителя передается
стенке в следствие теплопередачи. Этот
же поток тепла передается через стенку
в следствие теплопроводности. Далее он
передается хладоагенту в следствие
теплоотдачи
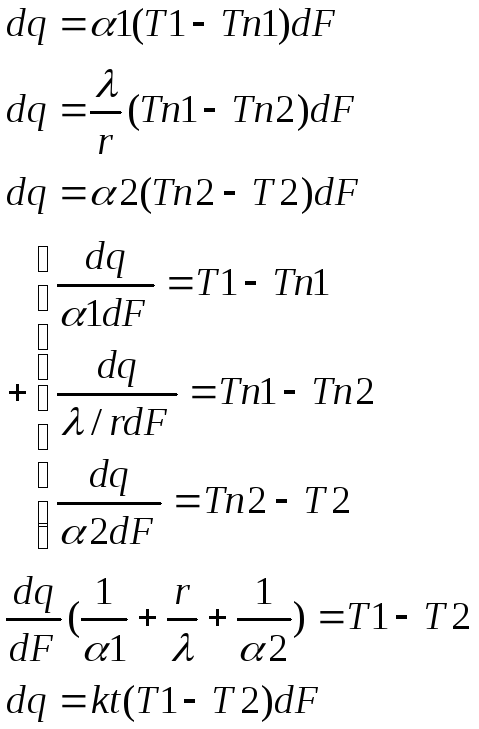
kt – коэффициент теплопередачи
Излучение – передача тепла электромагнитными волнами, единственный вид теплопереноса, не требующий теплопередающей среды
![]()
kn – коэффициент излучения
T1 – температура излучающего тела
T2 – температура принимающего тела
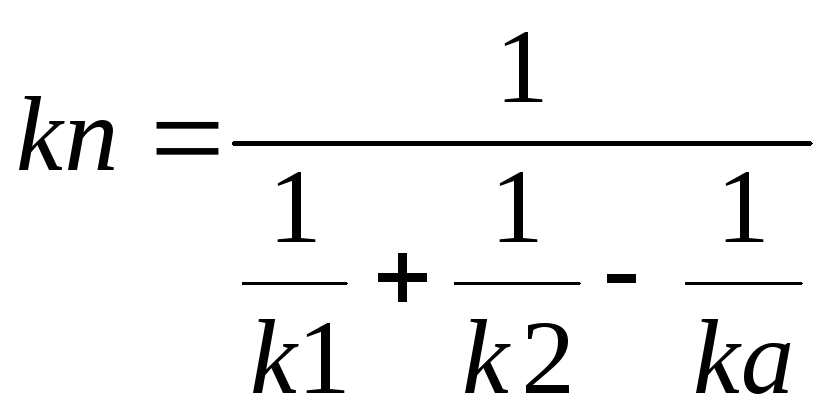 ,
кa
– для абсолютно черного тела
,
кa
– для абсолютно черного тела
2 Вариант-
Если
в объекте протекают тепловые процессы
(теплообмен с внешней средой, выделение
или поглощение тепла вследствие
химических реакций) - необходимо
использовать уравнения кинетики
теплопереноса. Основное уравнение
теплопередачи:
![]() (1.28),
где кт
- коэффициент теплопередачи; t
- разность температур.
(1.28),
где кт
- коэффициент теплопередачи; t
- разность температур.
Уравнение
теплопроводности, учитывающее
распространение тепла в твердых телах
и в тонких слоях жидкостей или газов,
имеет вид
![]() (1.29), где dq - количество тепла, переданного
теплопроводностью в единицу времени,
- коэффициент теплопроводности; t
- градиент температуры.
(1.29), где dq - количество тепла, переданного
теплопроводностью в единицу времени,
- коэффициент теплопроводности; t
- градиент температуры.
Перенос
тепла от границы раздела фаз в ядро
потока описывается уравнением теплоотдачи:
![]() (1.30),
гдеt
- коэффициент теплоотдачи, tп
- температура на поверхности; tя
- температура в ядре потока.
(1.30),
гдеt
- коэффициент теплоотдачи, tп
- температура на поверхности; tя
- температура в ядре потока.
Пусть,
например, в реакторе с мешалкой протекает
экзотермическая реакция
![]() ,
тепловой эффект которой равен Qр
[Дж/моль]. Для отвода тепла реактор
охлаждают хладагентом, подаваемым в
рубашку. Уравнение теплового баланса
в этом случае будет иметь следующий
вид:
,
тепловой эффект которой равен Qр
[Дж/моль]. Для отвода тепла реактор
охлаждают хладагентом, подаваемым в
рубашку. Уравнение теплового баланса
в этом случае будет иметь следующий
вид:
![]() (1.31),
где dQ - изменение тепла в объеме реактора,
qвх
- поток тепла, поступающий с исходным
веществом; qвых
- поток тепла, уходящий с продуктами
реакций, qт
- поток тепла, уходящий вследствие
теплообмена; qр
- поток тепла, выделяющегося в
экзотермической реакции.
(1.31),
где dQ - изменение тепла в объеме реактора,
qвх
- поток тепла, поступающий с исходным
веществом; qвых
- поток тепла, уходящий с продуктами
реакций, qт
- поток тепла, уходящий вследствие
теплообмена; qр
- поток тепла, выделяющегося в
экзотермической реакции.
Распишем
тепловые потоки:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
где сt - теплоемкость,
- плотность реакционной среды, vвх, vвых
- объемный расход реакционной среды,
соответственно, на входе и выходе
реактора; Твх, Т - температура реакционной
среды на входе и выходе реактора; Тт -
температура хладагента.
,
где сt - теплоемкость,
- плотность реакционной среды, vвх, vвых
- объемный расход реакционной среды,
соответственно, на входе и выходе
реактора; Твх, Т - температура реакционной
среды на входе и выходе реактора; Тт -
температура хладагента.
Подставив тепловые потоки в уравнение (1.31) и приняв, что vвх = vвых = v , получим:
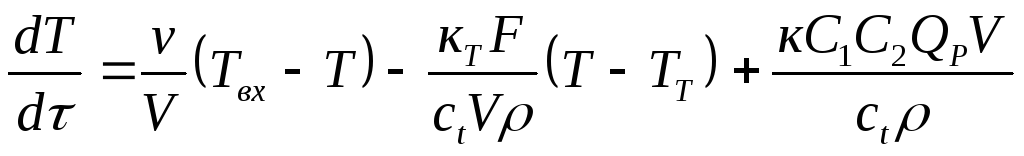 (1.32).
(1.32).
Рассмотрим другой пример. Пусть в трубчатом реакторе протекают реакции
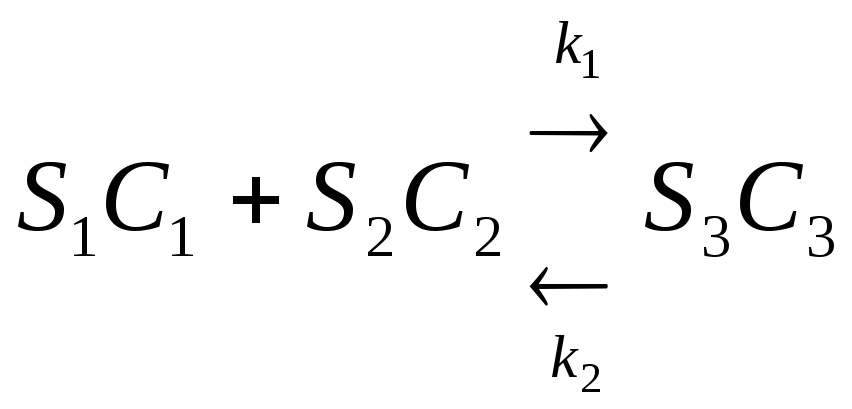 (1);
(1);
![]() (2)
(2)
Причем реакция (2) эндотермическая и ее тепловой эффект Qp3. Для поддержания заданной скорости протекания процесса реактор обогревают теплоносителем.
Уравнение
теплового баланса имеет вид:
![]() (1.33).
Распишем тепловые потоки:
(1.33).
Распишем тепловые потоки:![]() ,
,![]() ,
,![]() ,
,
где
V
- объем элементарного фрагмента трубы
реактора длиной l;
F
- площадь теплообмена элементарного
фрагмента трубы.
![]() ,
где D - диаметр трубы реактора. После
подстановок в (1.33) и сокращений наl
получим:
,
где D - диаметр трубы реактора. После
подстановок в (1.33) и сокращений наl
получим:
![]() (1.34)
(1.34)
