5-показатель адиабаты

5

Лабораторная работа

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА

Задание

1. Определить показатель адиабаты воздуха методом Клемана-Дезорма.

2. Сравнить полученное значение показателя адиабаты с его теоретическим значением и сделать вывод о точности проведенных измерений и достоверности использованного метода.

Приборы и принадлежности

Установка для определения показателя адиабаты воздуха с манометром и насосом.

Общие сведения

Адиабатическим называется процесс, совершаемый термодинамической системой, при котором отсутствует теплообмен между этой системой и внешней средой.

Уравнение, описывающее состояние системы в адиабатическом процессе, имеет вид:

, (1)

где и – давление и объем газа; – показатель адиабаты.

Показатель адиабаты – это коэффициент, численно равный отношению теплоемкостей газа при постоянном давлении и при постоянном объеме :

. (2)

Физический смысл его заключается в том, что он показывает, во сколько раз количество теплоты, необходимой для нагревания газа на 1 К в изобарическом процессе (), больше количества теплоты, необходимой для той же цели в изохорическом процессе ().

Для идеального газа показатель адиабаты определяется по формуле:

, (3)

где i – число степеней свободы молекул газа.

Совершение газом адиабатического процесса требует его идеальной термоизоляции, что в реальных условиях не вполне достижимо. Тем не менее будем считать, что в данной работе экспериментальная установка позволяет осуществить адиабатический процесс.

Описание установки

Установка (рис. 1) для определения показателя адиабаты воздуха состоит из стеклянного сосуда 1, жидкостного манометра 2 и насоса 3, соединенных резиновыми и стеклянными трубками. Горловина сосуда закрыта пробкой с краном 4 для сообщения сосуда с атмосферой. Насос позволяет изменять давление в сосуде при закрытом кране, а манометр - измерять это изменение.

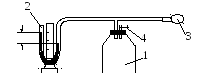
h

Рис. 1

Теория метода

Все изменения состояния воздуха в процессе эксперимента качественно представлены на рис. 2.

Рис. 2

Суть эксперимента заключается в переводе воздуха в разные состояния различными процессами и анализе качественных изменений этих состояний (точнее - изменений давления воздуха в сосуде). Исходное состояние (точка 0) воздуха в сосуде (кран 4 открыт) характеризуется давлением p₀ , равным атмосферному, объемом V₀ и температурой T₀, равной температуре окружающей среды.

Закрыв кран, создают насосом в сосуде избыточное давление: при этом воздух, испытывая адиабатическое сжатие, переходит в первое состояние (точка 1). Это состояние характеризуется параметрами , и , при этом и (адиабатическое сжатие газа сопровождается его нагреванием).

После прекращения работы насоса вследствие теплообмена через стенки сосуда температура газа снижается до первоначальной температуры , что вызывает некоторое снижение его давления. В результате в сосуде устанавливается давление, превышающее атмосферное давление на некоторое значение . Это второе состояние газа (точка 2) характеризуется параметрами , и .

Если кран кратковременно открыть и закрыть, то газ в сосуде адиабатически расширится (так как теплообмен произойти не успеет), и его давление практически мгновенно выровняется с атмосферным давлением. Это третье состояние газа (точка 3) характеризуется параметрами , и , при этом (адиабатическое сжатие газа сопровождается его охлаждением).

Сразу после закрытия крана в сосуде начинается изохорический процесс нагревания воздуха путем теплообмена с внешней средой, сопровождающийся некоторым повышением его давления. В результате в сосуде устанавливается давление, повышенное по сравнению с атмосферным давлением на некоторое значение . Это четвертое состояние газа (точка 4) характеризуется параметрами , и .

Показатель адиабаты полностью определяется значениями избыточных давлений и .

Для состояний 2 и 3 выполняется соотношение, получающееся при выводе уравнения состояния газа в адиабатическом процессе:

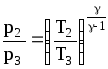. (4)

Для состояний 3 и 4 с помощью уравнения Клапейрона–Менделеева можно получить соотношение (закон Шарля):

. (5)

С учетом того, что , , , подставляя выражение (4) в (3), получим:

. (6)

Логарифмируя последнее выражение, получим:

. (7)

Известно, что при . С учетом этого можно записать, что

, (8)

откуда следует, что

. (9)

Избыточное давление в сосуде, измеряемое манометром, пропорционально разности уровней h жидкости в обоих коленах трубки манометра (см. рис. 2). С учетом этого обстоятельства выражение (9) примет окончательный вид:

. (10)

Отсчет уровней производится с учетом кривизны поверхности жидкости в трубке. Для отсчета берется деление шкалы, совпадающее с касательной к поверхности жидкости.

Порядок выполнения работы

1. При закрытом кране насосом создать избыточное давление в сосуде (необходимо избегать резких движений, так как жидкость может быть легко вытолкнута из трубки манометра).

2. Выждать, пока уровни жидкости в манометре перестанут изменять свое положение, и произвести отсчет их разности h₁ .

3. Открыть кран для выпуска воздуха и быстро его закрыть в момент первого пересечения уровнями жидкости исходного их положения (до накачки насосом).

4. Выждать, пока уровни жидкости в манометре перестанут изменять свое положение, и произвести отсчет их разности h₂ .

5. Эксперимент необходимо повторить не менее 5 раз, и полученные результаты занести в таблицу 1.

Таблица 1

№ п/п	1	2	3	4	5
h1 , мм
h2 , мм

6. По формуле (10) вычислить оценку показателя адиабаты, использовав средние значения ()разностей уровней жидкости в манометре.

7. Рассчитать погрешности измерения показателя адиабаты воздуха.

8. Сравнить полученный доверительный интервал значений показателя адиабаты с его теоретическим значением и сделать вывод о точности проведенных измерений и достоверности использованного метода.

Вычисление погрешностей

1. В этой работе велика роль случайных погрешностей, поэтому приборными погрешностями, ввиду их относительной малости, следует пренебречь.

Случайные погрешности рассчитываются по методу Стьюдента.

2. Полная относительная погрешность измерения показателя адиабаты:

.

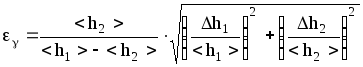3. Полная абсолютная погрешность измерения показателя адиабаты:

.

Полученный результат округляется и записывается в виде:

; ; .

Правильность проведенных измерений и вычислений должна подтверждаться "перекрытием" полученного доверительного интервала для значения показателя адиабаты воздуха и его теоретического значения.

Контрольные вопросы

1. Дайте определения изохорическому, изобарическому и изотермическому процессам. Изобразите эти процессы графически в координатных осях p-V . Запишите уравнение состояния идеального газа в этих процессах и поясните смысл входящих в них физических величин.

2. Дайте определение адиабатическому процессу. Изобразите этот процесс графически в координатных осях p-V. Запишите уравнение состояния газа в этом процессе (уравнение Пуассона) и поясните смысл входящих в него физических величин.

3. Что такое показатель адиабаты? Как определить его теоретическое значение ?

4. Опишите состав экспериментальной установки и порядок действий при определении показателя адиабаты воздуха.

5. Сформулируйте первый закон термодинамики.

6. Что такое внутренняя энергия вещества? Чему равна внутренняя энергия идеального газа в различных изопроцессах?

7. Дайте определение теплоемкости вещества. Что такое удельная и молярная теплоемкости вещества? Чему равна молярная теплоемкость идеального газа в различных изопроцессах ?

8. Как вычислить работу, совершаемую идеальным газом, в изохорическом, изотермическом, изобарическом и адиабатическом процессах ?

9. Как вычислить изменение внутренней энергии идеального газа при совершении им изохорического (изобарического, изотермического, адиабатического) процессов ?

10. Как определить количество теплоты, получаемой (или отдаваемой) идеальным газом при совершении им изохорического (изобарического, изотермического, адиабатического) процессов?