Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тамбовский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Konspekt_lektsy_MSP.doc

Скачиваний:

Добавлен:

21.05.2015

Размер:

3.57 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

1. Структура и состав элементов системы массового обслуживания.

При описании и анализе систем массового обслуживания (СМО) используется специальная терминология. Основными элементами СМО являются источник, генерирующий поток заявок на обслуживание, накопитель, обеспечивающий размещение в нем очереди заявок, ожидающих обслуживания и, наконец, каналы, или приборы, в которых производится процесс обслуживания заявок.

Принципиальная структура СМО приведена на рис. 1.

Рис. 1. Схема системы массового обслуживания

Из этой схемы видно, что обслуженные заявки могут снова возвращаться в источник, откуда поступать для нового обслуживания.

В общем случае в состав СМО может входить несколько источников, генерирующих потоки заявок, несколько накопителей-приборов обслуживания, связанных между собой. Такую систему называют сетью массового обслуживания. С помощью сетей МО могут моделироваться сети ЭВМ, автоматизированные системы управления в случае, когда в их состав входит совокупность объектов АСУ, связанных каналами передачи данных, различного рода коммуникационные системы, например, система воздушного движения, включающая совокупность аэропортов и связывающих их воздушных трасс.

Свойства СМО определяются ее структурой и характеристиками входящих в СМО элементов, в первую очередь источника, генерирующего поток заявок, и каналов, осуществляющих их обслуживание. Рассмотрим свойства и математические модели этих элементов

2. Источники и потоки заявок.

Под источником понимается любой объект, генерирующий заявки на обслуживание. На объекте АСУ это может быть оператор автоматизированного рабочего места, программа, выполняемая в ЭВМ КСА, некоторый источник прерываний (таймер, схема или программа контроля и т. д.). Различают два вида источников:

1) источники, у которых характеристики генерируемого потока заявок не зависят от процессов в системе обслуживания;

2) источники, поведение которых (т.е. свойства генерируемых ими потоков заявок) зависит от того, как происходит обслуживание заявок этих потоков.

Источники первого типа называются бесконечными, второго типа — конечными. Соответственно СМО по своей структуре делятся на разомкнутые и замкнутые.

Поток заявок, поступающих из источника на вход накопителя СМО, представляет последовательность событий (zn tn), где zn— заявка с номером п, п = 1, 2, 3,..., tn — момент ее возникновения. В теории СМО моменты t1 t2,... возникновения заявок zi, рассматриваются как случайные моменты времени, поэтому поток заявок определяется как случайный процесс, задаваемый функцией распределения интервалов времени между соседними заявками

Предполагается, что каждый интервал n представляет случайную величину, описываемую функцией распределения

где t — независимая переменная.

Поток заявок может быть нестационарным, если его характеристики изменяются во времени, и стационарным в противном случае. В реальных системах потоки заявок на входе СМО, как правило, нестационарны, поскольку их интенсивность зависит от конкретной ситуации, времени суток и года и т. д. Однако характеристики процессов обслуживания в СМО наиболее просто определяются для стационарных потоков, поэтому нестационарные действительные потоки при анализе аппроксимируются на отдельных интервалах времени стационарными.

Важнейшей вероятностной моделью входного потока заявок является модель в виде простейшего потока, т. е. в виде стационарного пуассоновского процесса. Для простейшего потока вероятность того, что в интервале времени Т поступит ровно k заявок, определяется распределением Пуассона

(4.1)

где  — параметр, называемый интенсивностью потока заявок.

Для простейшего потока, описываемого распределением (4.1), интервалы  между соседними моментами заявок представляют независимые, случайные величины, подчиненные показательному закону распределения с плотностью

(4.2)

Математическое ожидание и дисперсия для распределения (4.2) равны:

Простейший поток, помимо стационарности, обладает следующими свойствами:

— отсутствием последействия, проявляющего в том, что длина интервала  до момента поступления следующей заявки не зависит от того, поступила или нет заявка в рассматриваемый начальный момент времени;

— ординарностью, состоящей в том, что в каждый малый интервал времени может поступить не более одной заявки.

Рассмотрим указанные свойства более подробно. Образно говоря, отсутствие последствия показательно распределенного интервала времени состоит в том, что «возраст» интервала никак не влияет на величину оставшегося времени его «жизни». Пусть заявка поступила в момент t= 0. Распределение длины интервала до поступления следующей заявки описывается выражением

Пусть, далее, с момента t = 0 прошло То секунд и не поступило ни одной заявки. Возникает вопрос: «Какова вероятность того, что следующая заявка поступит через t секунд, считая от момента Т0?». На основании теоремы о произведении вероятностей здесь имеем

(4.3)

Назовем величину интервала  длительностью «жизни» интервала, величину То — «возрастом» интервала, а разность -То — остаточным временем жизни интервала. Соотношение (4.3) выражает тот факт, что для интервала, длительность жизни которого распределена по показательному закону, остаточное время жизни интервала -То имеет то же самое распределение.

Рассматриваемое свойство показательного распределения объясняется замечательным свойством показательной функции exp(-t) состоящей в том, что любой ее «хвост» имеет с точностью до постоянного множителя форму самой функции, сдвинутой на соответствующую величину вправо по оси абсцисс. Действительно, пусть длина интервала имеет показательное распределение f(t)=exp(-t), а возраст равен Tо. Для того чтобы определить распределение остаточного времени интервала, нужно рассмотреть значения функции f(t) для t>T0.

Разделим все ординаты «хвоста» функции exp(-t), для t>T0 на площадь этого хвоста равную, очевидно, вероятности Р[>T0]. Эта операция тождественна операции вычисления условного распределения путем деления вероятности совместного события (Т0< <t + To) на вероятность условия, т. о. события (>T0). Получающая в результате деления функция

представляет точную копию исходной функции f(t), но сдвинутую из нулевой точки вправо на Tо единиц времени, т. е. функцию

Полученный результат подтверждает свойство ординарности-простейшего потока, состоящее в том, что вероятность попадания в короткий интервал 0 двух и более заявок для простейшего потока много меньше вероятности попадания одной заявки, равной.

В теории массового обслуживания наибольшее число результатов получено именно для простейшего входного потока заявок. Это обстоятельство, а также тот факт, что простейший поток в силу своей предельной нерегулярности создает наиболее тяжелый режим работы для СМО, привели к тому, что анализ процессов функционирования СМО, как правило,, рассматривается именно для этого типа входного потока.

Контрольные вопросы:

Назовите основные элементы системы массового обслуживания?
Назовите типы источников заявок в СМО?
Какими свойствами обладает простейший поток заявок?

Тема № 3 «Модели и свойства элементарных систем массового обслуживания»

Лекция № 7 «Процессы в системах массового обслуживания»

Цель лекции.

а) учебная цель:

Целью является формирование у слушателей целостного представления о принципах применения элементов теории вероятностей при моделировании сетевых процессов – элемента систем массового обслуживания.

План лекции.

Длительность обслуживания заявок
Характеристики процессов в СМО

Длительность обслуживания заявок.

Длительность обслуживания заявки на обработку данных в КСА определяется временем, необходимым процессору для исполнения соответствующей программы или совокупности программ, реализующих задачу обработки данных. В общем случае длительность обслуживания — случайная величина _об с определенным законом распределения, различным для различных типов заявок. Предполагается, что длительности обслуживания различных последовательно исполняемых заявок независимы. Степень случайности длительности обслуживания зависит от степени разветвленности программы и от степени разнообразия исходных данных.

Пусть плотность распределения длительности обслуживания описывается произвольным законом распределения f_об(t) с математическим ожиданием М [_об] = _об. Для исследования и описания процессов в СМО необходимо иметь функцию f_об(t) в аналитическом виде. С этой целью функция f_об(t), если она найдена экспериментально, аппроксимируется некоторым типовым законом распределения.

В случае, когда из характеристик длительности обслуживания известно только математическое ожидание _об, вероятностные свойства _об аппроксимируются показательным распределением

Такая аппроксимация оказывается справедливой в случае, когда программа, исполняемая по заявке, имеет большое число разветвлений различной протяженности, причем вероятность развития процесса по коротким ветвям больше, чем более протяженным.

Оказывается, что ряд аналитических зависимостей для процессов в СМО может быть получен для произвольного закона-, распределения длительности обслуживания заявок, относительно которого известны две его характеристики: математическое ожидание _об и второй начальный момент _об. Именно такое допущение будет использоваться ниже при анализе дисциплин обслуживания заявок.

Характеристики процессов в СМО.

СМО типа М | М | 1 представляет разомкнутую одноканальную систему массового обслуживания с «чистым» ожиданием,. т.е. с неограниченной длиной очереди. На вход системы поступает простейший поток заявок. Пусть его интенсивность равна,  заявок в секунду. Время обслуживания _об распределено по показательному закону со средним значением .

Процессы обслуживания в рассматриваемой СМО характеризуются следующими величинами:

— вероятностью р{п), п = 0, 1, 2, что в системе находится ровно п заявок;

— средним числом заявок, находящихся в очереди (п_оч), на обслуживании (п_об) и в целом в системе (п);

— средними значениями времени ожидания , времени обслуживания, времени пребывания.

Представляет интерес среднее значение случайной величины

n_о6 = п — n_оч,

т. е. среднее значение числа заявок, находящихся на обслуживании. Эта случайная величина принимает значения 0 и 1 с вероятностями

где - загрузка системы.

Таким образом, среднее число заявок, находящихся в СМО М|М|1 на обслуживании, численно равно загрузке .

Система М|G|1 представляет собой одноканальную СМО с пуассоновским входным потоком и произвольным (общим) распределением времени обслуживания. Считаются заданными следующие параметры системы:

— интенсивность  входного пуассоновского потока заявок:

— математическое ожидание и второй начальный момент времени обслуживания.

Таким образом, сам закон распределения времени обслуживания предполагается неизвестным.

Центральным вопросом исследования свойств СМО М | G \ 1 является определение среднего времени ожидания по характеристикам. В основе решения задачи лежит анализ свойств случайной величиныY — оставшегося времени обслуживания заявки, уже находящейся на обслуживании, на момент прихода в систему новой заявки.

Пусть в канале СМО протекает процесс обслуживания заявок со средним временем обслуживания . В произвольный момент времениt_n на вход СМО поступает заявка z_n и застает канал СМО занятым обслуживанием некоторой заявки z_ii<n, поступившей ранее. Спрашивается, чему должно быть равно среднее время дообслуживания заявки z_i? На первый взгляд кажется, что среднее время дообслуживания должно бить равно /2. Оказывается такой ответ неверен. Предположим, что время обслуживания распределено по показательному закону со средним значением . Благодаря свойству отсутствия последействия, время дообслуживания заявкиz_i, застигнутой на обслуживании заявкой z_n, не зависит от того, сколько времени уже протекает обслуживание z_i и распределено так же, как и полная длительность ее обслуживания. В этом случае среднее время дообслуживания заявки z_i будет равно среднему времени ее обслуживания , а не 0,5!

Объяснение полученного парадокса состоит в том, что вероятности встречи заявки z_n с другими заявками в интервале их обслуживания в канале СМО неравнозначны. Ясно, что у нлямкн z_n больше шансов застать на обслуживании в СМО м.чяику z_i, имеющую «большую» длительность обслуживания.

Поэтому закон распределения длительности времени обслуживания заявки z_i застигаемой заявкой z_n оказывается отличным от закона распределения случайной величины .

Интервал времени обслуживания заявки z_i застигаемой на обслуживании заявкой z_n назовем «отобранным интервалом». Введем понятия длительность жизни Т, возраста Т_о и остаточного времени жизни Y отобранного интервала (рис. 1).

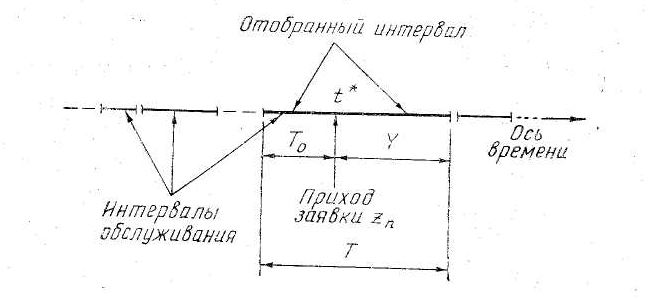
Рис. 1

Отобранный интервал описывается выражением:

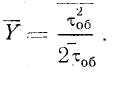
Таким образом, среднее значение Y остаточного времени численно равно второму начальному моменту времени обслуживания, деленному на удвоенное среднее значение времени обслуживания.