
- •Содержание
- •Глава 1. Приближенные методы решения обыкновенных дифферен-циальных уравнений……………………………………………………………5
- •Глава 2. Приближенные методы решения дифференциальных уравне-
- •Глава 3. Приближенные методы решения интегральных уравне-
- •Глава 4. Статистическая обработка данных………………………………40
- •Примерный тематический план проведения лабораторных работ
- •Глава 1. Приближенные методы решения обыкновенных дифферен-циальных уравнений
- •1.1. Справочные материалы по приближенным методам решения обыкновенных дифференциальных равнений
- •1.1.1. Постановка задачи Коши
- •1.1.2. Метод последовательных приближений
- •1.1.3. Метод Эйлера
- •1.1.6.Многошаговые методы. Метод Адамса. Методы прогноза–коррекции
- •1.1.7. Постановка краевой задачи для обыкновенного дифференциального уравнения
- •1.1.8. Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей
- •1.1.8. Приближенное решение обыкновенных дифференциальных уравнений методом прогонки
- •1.2. Лабораторная работа № 1. Приближенное решение обыкновен-ных дифференциальных уравнений методом последовательных прибли-жеий.
- •1.3. Лабораторная работа № 2. Приближенное решение обыкно-
- •1.4. Лабораторная работа № 3. Приближенное решение обыкновенных дифференциальных уравнений. Метод Адамса. Методы прогноза-коррекции.
- •1.5. Лабораторная работа № 4 Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей.
- •1.6. Лабораторная работа № 5. Приближенное решение обыкновенных дифференциальных уравнений методом прогонки
- •Глава 2 Приближенные методы решения дифференциальных уравнений с частными производными
- •2.1. Справочный материал по приближенным методам решения дифференциальных уравнений с частными производными
- •2.1.1. Постановка задачи Дирихле. Приближенное решение уравнения Лапласа.
- •2.1.2. Итерационный метод решения системы конечно-разностных уравнений (процесс усреднения Либмана)
- •2.2. Лабораторная работа № 6. Метод сеток для задачи Дирихле.
- •2.3. Лабораторная работа № 7. Итерационный метод решения системы конечно-разностных уравнений (процесс усреднения Либмана)
- •Глава 2. Приближенные методы решения интегральных уравнений
- •3.1. Справочный материал по приближенным методам решения интегральных уравнений
- •3.2. Лабораторная работа № 8. Решение уравнения Фредгольма второго рода методом конечных сумм
- •Глава 4. Статистическая обработка данных
- •4.1. Справочный материал по статистической обработке данных
- •4.2. Лабораторная работа № 9. Методы обработки статистических
- •Список литературы
1.2. Лабораторная работа № 1. Приближенное решение обыкновен-ных дифференциальных уравнений методом последовательных прибли-жеий.
Задания:
1) Найти три
последовательных приближения решения
обыкновенного дифференциального
уравнения, если
![]() .
.
2) Найти три
последовательных приближения решения
системы обыкновенных дифференциальных
уравнений, если
![]() ,
,
![]() .
.
3) Методом
последовательных приближений найти
приближенное решение дифференциального
уравнения на отрезке [0; 0,8] с точностью
до 10-3, полагая![]() .
.
Варианты заданий к лабораторной работе № 1
№ 1
1)![]() . 2)
. 2)
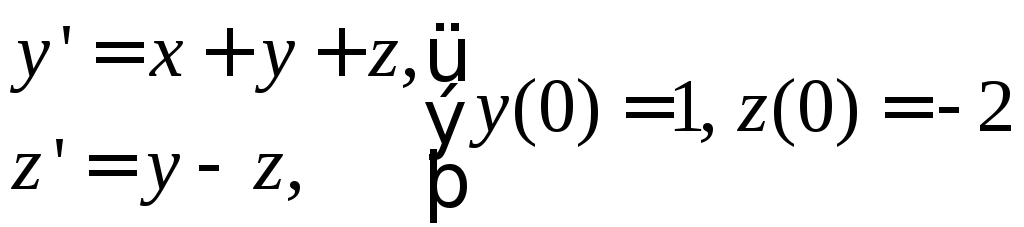 .
.
3)
![]() .
.
№ 2
1) ![]() . 2)
. 2)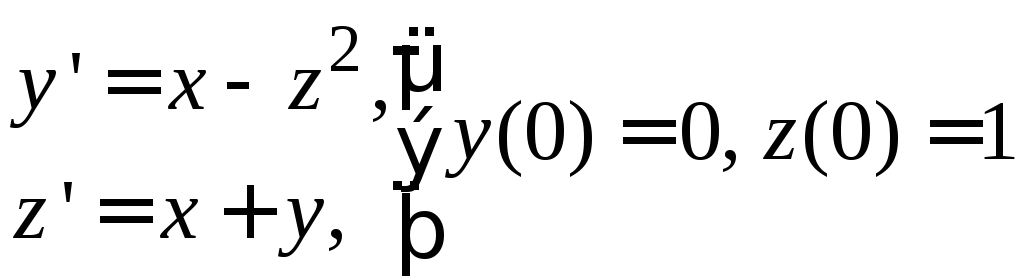
3) ![]() .
.
№ 3
1) ![]() . 2)
. 2)
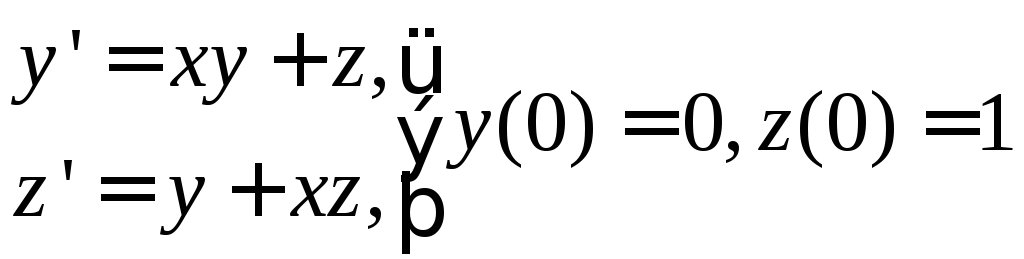
3)
![]() .
.
№ 4
1) ![]() . 2)
. 2)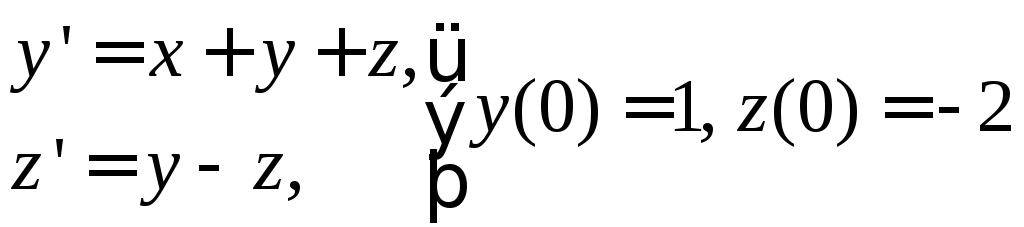 .
.
3)
![]() .
.
№ 5
1) ![]() . 2)
. 2)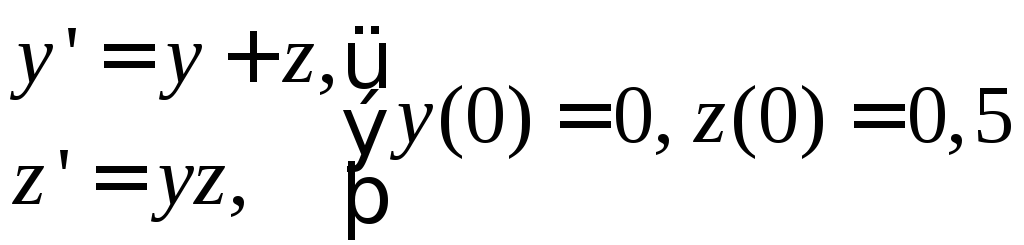 .
.
3)
![]() .
.
№ 6
1) ![]() . 2)
. 2)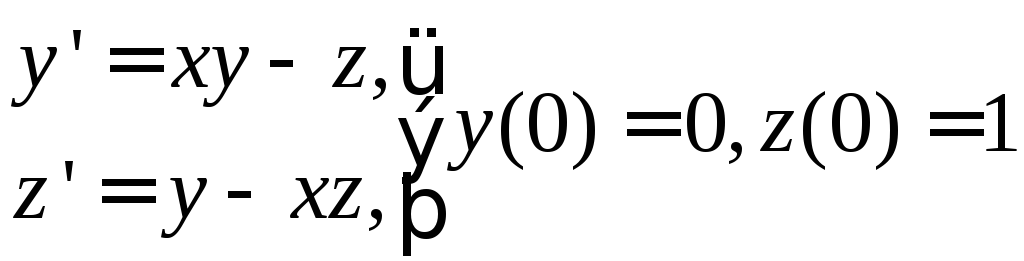 .
.
3)
![]() .
.
№ 7
1)
![]() . 2)
. 2)
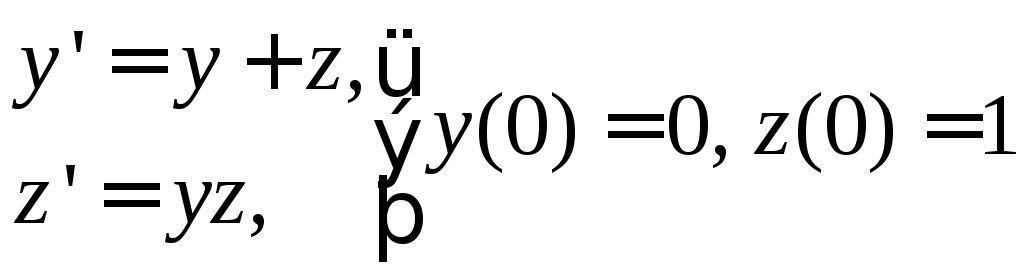 .
.
3) ![]() .
.
№ 8
1) ![]() . 2)
. 2)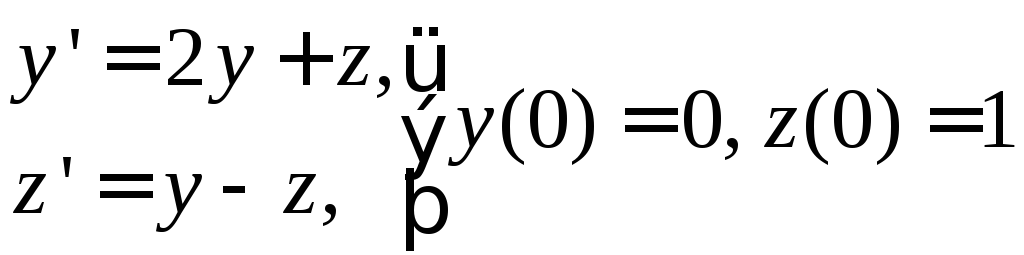 .
.
3) ![]() .
.
№ 9
1)![]() . 2)
. 2)
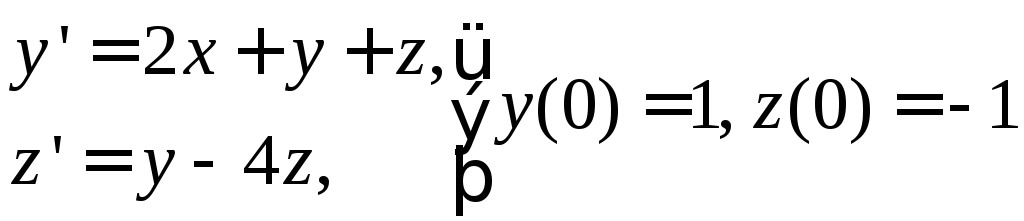 .
.
3)
![]() .
.
№ 10
1) ![]() . 2)
. 2)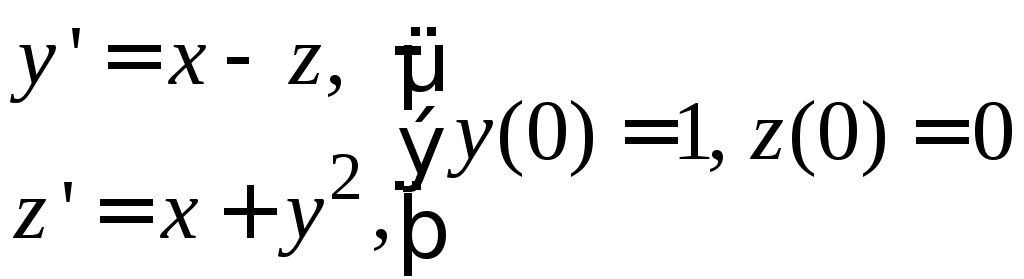
3) ![]() .
.
№ 11
1) ![]() . 2)
. 2)
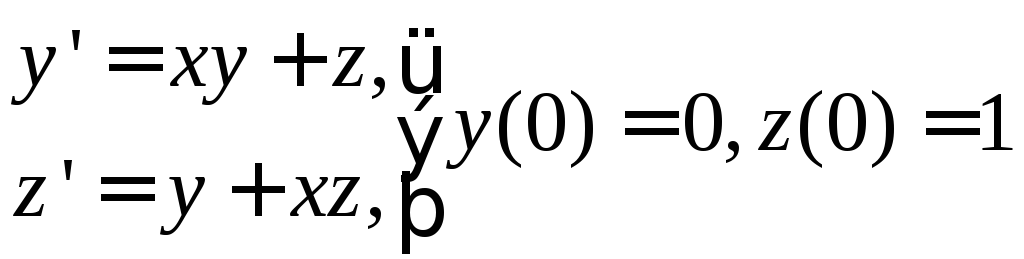
3)
![]() .
.
№ 12
1) ![]() . 2)
. 2)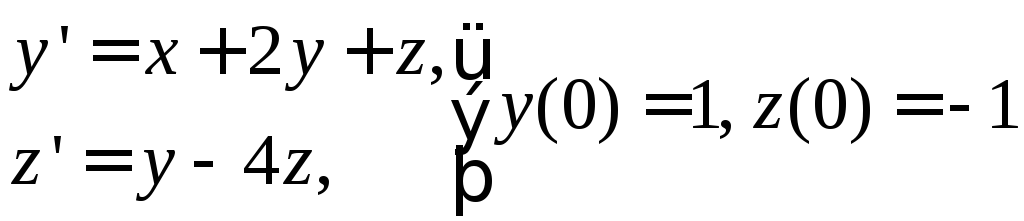 .
.
3)
![]() .
.
№ 13
1) ![]() . 2)
. 2)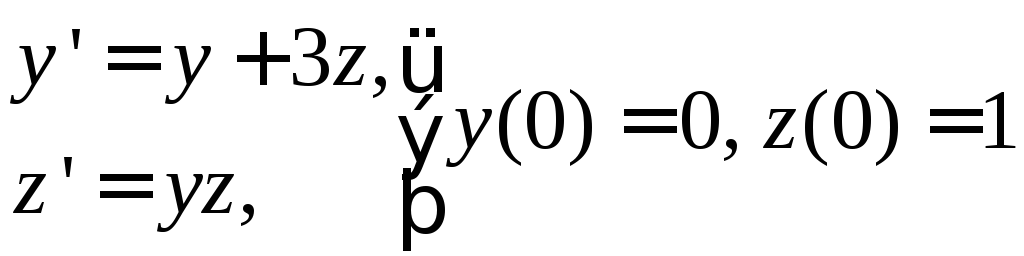 .
.
3)
![]() .
.
№ 14
1) ![]() . 2)
. 2)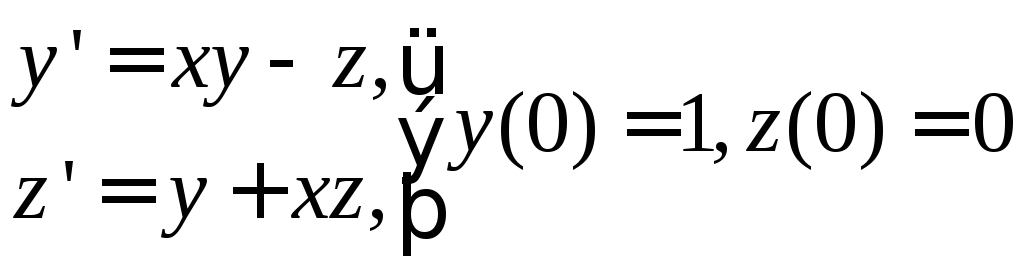 .
.
3)
![]() .
.
№ 15
1)
![]() . 2)
. 2)
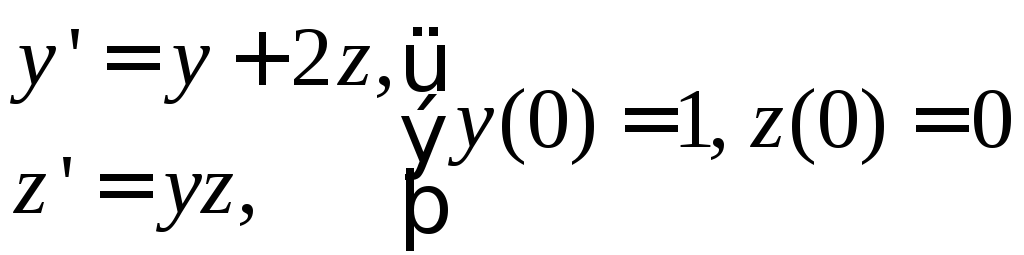 .
.
3) ![]() .
.
№ 16
1) ![]() . 2)
. 2)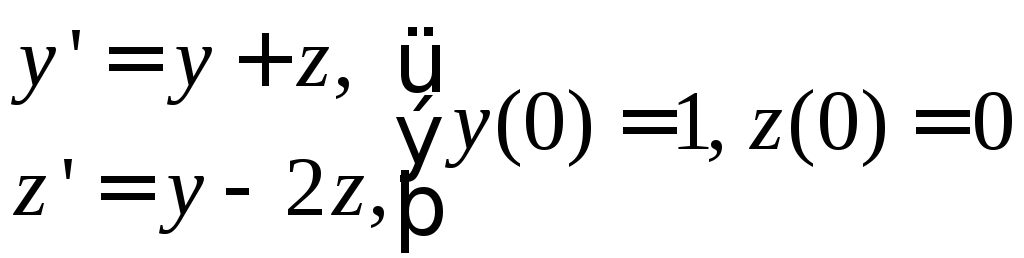 .
.
3) ![]() .
.
1.3. Лабораторная работа № 2. Приближенное решение обыкно-
венных дифференциальных уравнений. Методы Эйлера, Эйлера–Коши, Рунге–Кутта
Задания:
1) Найти приближенное
решение уравнения
![]() на отрезке
на отрезке
[x0,x0+H]
при начальном условии![]() и заданном числеnделений
исходного отрезка методом Эйлера,
Эйлера-Коши, Рунге-Кутта четвертого
порядка.
и заданном числеnделений
исходного отрезка методом Эйлера,
Эйлера-Коши, Рунге-Кутта четвертого
порядка.
2) Используя метод
двойного пересчёта, оценить погрешность
методов в последней точке отрезка
![]() .
.
Варианты заданий к лабораторной работе № 2
№ 1.
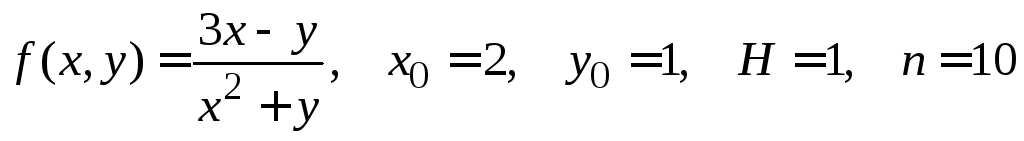 .
.
№ 2.
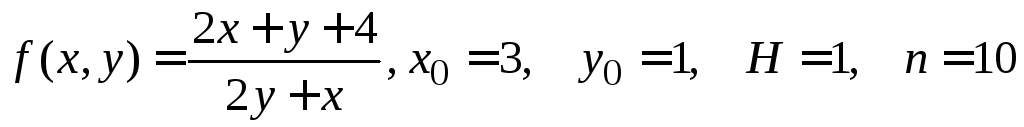 .
.
№ 3.
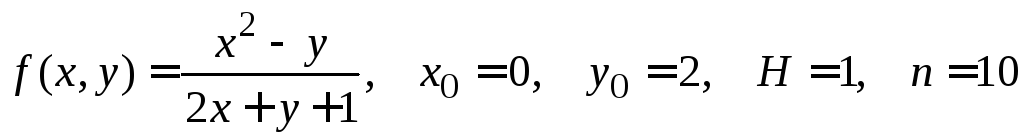 .
.
№4.
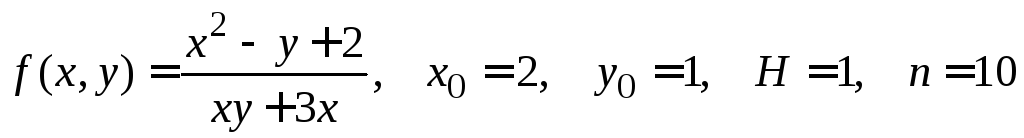 .
.
№5.
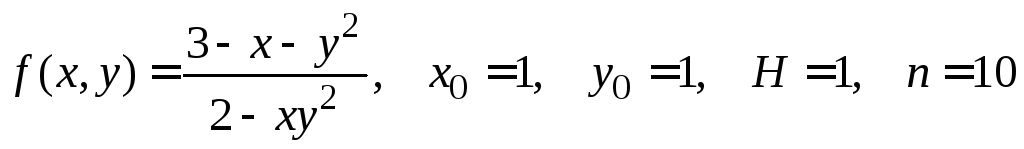 .
.
№ 6.
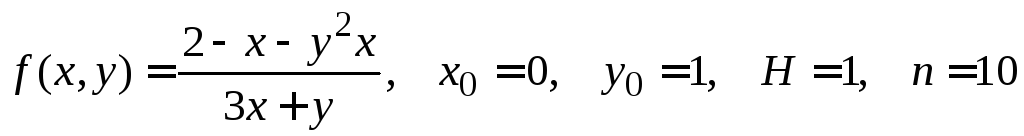 .
.
№ 7.
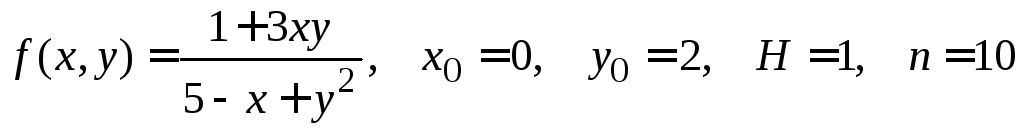 .
.
№ 8.
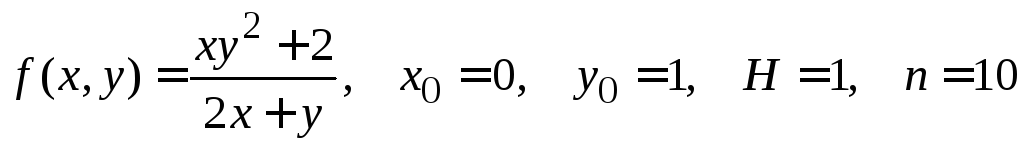 .
.
№ 9.
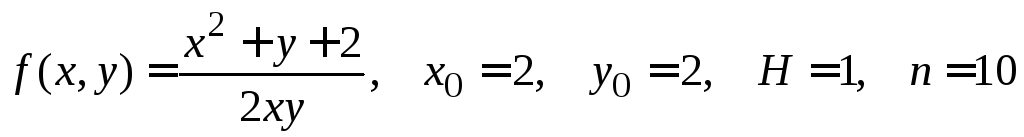 .
.
№ 10.
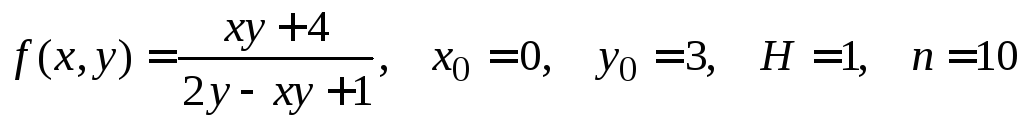 .
.
№ 11.
![]() .
.
№ 12.
![]() .
.
№ 13.
![]() .
.
№ 14.
![]() .
.
№ 15.
![]() .
.
№ 16.
![]() .
.
1.4. Лабораторная работа № 3. Приближенное решение обыкновенных дифференциальных уравнений. Метод Адамса. Методы прогноза-коррекции.
Задания:
1) Используя метод
Адамса четвертого порядка, составить
таблицу значений решения задачи Коши
для дифференциального уравнения
![]() ,
удовлетворяющего начальным условиям
,
удовлетворяющего начальным условиям![]() на отрезке [0,1] с шагомh=0,1.
Начальные значения определить методом
Рунге-Кутта четвертого порядка.
Окончательные результаты вычислений
сохранить с точностью до 10-4.
на отрезке [0,1] с шагомh=0,1.
Начальные значения определить методом
Рунге-Кутта четвертого порядка.
Окончательные результаты вычислений
сохранить с точностью до 10-4.
2) Используя метод
прогноза-коррекции составить таблицу
значений решения задачи Коши для
дифференциального уравнения
![]() ,
удовлетворяющего начальным условиям
,
удовлетворяющего начальным условиям![]() на отрезке [0,1] с шагомh=0,1.
Начальные значения определить методом
Рунге-Кутта четвертого порядка. На
каждом шаге коррекции выполнять только
одну итерацию. Результаты вычислений
сохранить с точностью до 10-4.
на отрезке [0,1] с шагомh=0,1.
Начальные значения определить методом
Рунге-Кутта четвертого порядка. На
каждом шаге коррекции выполнять только
одну итерацию. Результаты вычислений
сохранить с точностью до 10-4.
Варианты заданий к лабораторной работе № 3
|
№ 1. |
|
|
№ 2. |
|
|
№ 3. |
|
|
№ 4. |
|
|
№ 5. |
|
|
№ 6. |
|
|
№ 7. |
|
|
№ 8. |
|
|
№ 9. |
|
|
№ 10. |
|
|
№ 11. |
|
|
№ 12. |
|
|
№ 13. |
|
|
№ 14. |
|
|
№ 15. |
|
|
№ 16. |
|
1.5. Лабораторная работа № 4 Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей.
Задание:
Используя метод
конечных разностей, составить решение
краевой задачи для обыкновенного
дифференциального уравнения с шагом
![]() Вычисления вести с точностью до
Вычисления вести с точностью до![]() .
.
Варианты заданий к лабораторной работе № 4
|
№1. |
|
|
|
|
№2. |
|
|
|
|
№3. |
|
|
|
|
№4. |
|
|
|
|
№5. |
|
|
|
|
№6. |
|
|
|
|
№7. |
|
|
|
|
№8. |
|
|
|
|
№9. |
|
|
|
|
№10. |
|
|
|
|
№11. |
|
|
|
|
№12. |
|
|
|
|
№13. |
|
|
|
|
№14. |
|
|
|
|
№15. |
|
|
|
|
№16 |
|
|
|
